基于直升机航空重力同步地形的布格改正处理

doi:10.11720/wtyht.2023.1289

基于直升机航空重力同步地形的布格改正处理

屈进红^,¹^,², 姜作喜¹^,², 周锡华¹^,², 王明¹^,², 罗锋¹^,²

1.自然资源部航空地球物理与遥感地质重点实验室,北京 100083

2.中国自然资源航空物探遥感中心,北京 100083

Airborne Bouguer gravity based on synchronous terrains surveyed using helicopter airborne gravimetry

QU Jin-Hong^,¹^,², JIANG Zuo-Xi¹^,², ZHOU Xi-Hua¹^,², WANG Ming¹^,², LUO Feng¹^,²

1. Key Laboratory of Airborne Geophysics and Remote Sensing Geology,MNR, Beijing 100083,China

2. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources,Beijing 100083,China

第一作者: 屈进红(1981-),男,正高级工程师,主要从事航空重力测量与方法技术研究。Email:qunjant007@163.com

责任编辑: 王萌

收稿日期: 2022-06-10 修回日期: 2022-09-9

基金资助:

国家重点研发计划课题(2017YFC0601705)
国家重点研发计划课题(2017YFC0601706)

Received: 2022-06-10 Revised: 2022-09-9

摘要

重点勘探区内大规模的采矿活动从未间断过,矿山采空区、排土场和尾矿库等处在不断形变过程中。仍依靠搜集数字地形的方式,无法做到地形数据与航空重力测量数据的良好匹配,给航空重力地形改正和中间层改正带来极大的改正误差。本文通过直升机重磁测量系统的飞行GNSS大地高与无线电离地高度进行求差,再转换到正常高,最后经过调平和精细化处理获得同步实测地形。又与搜集的多种地形数据一起对比ICESat-2/ATL08星载激光高程,实测地形Wxd100和Wxd400的高程精度分别为5.33 m和8.93 m。使用实测地形进行航空重力布格改正后,矿区和多条典型测线的数据质量有了明显改善。

关键词： 航空重力测量; 同步; 实测地形; 布格重力; 矿山

Abstract

Large-scale mining activities have been continued in key exploration areas. Consequently, the mined-out areas, waste dumps, and tailings ponds of mines are constantly deforming. As a result, the digital terrain method fails to make the terrain data closely match the airborne gravimetric data, leading to serious correction errors in airborne gravity terrain correction and stone-slab correction. This study calculated the difference between the GNSS geodetic height and the radio terrain clearance altitude of the helicopter gravity and magnetic survey system and then converted the GNSS geodetic height into normal height. Then, the synchronous surveyed terrains were obtained through leveling and fine-scale processing. Moreover, the surveyed terrain data, together with various collected terrain data, were compared with the ICESat-2/ATL08 spaceborne laser elevation. The results show that the surveyed terrains Wxd100 and Wxd400 had elevation precision of 5.33 m and 8.93 m, respectively. After airborne Bouguer gravity correction was conducted using the surveyed terrains, the data quality of the mining area and several typical survey lines was greatly improved.

Keywords： airborne gravimetry; synchronization; surveyed terrain; Bouguer gravity; mine

PDF (6569KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

屈进红, 姜作喜, 周锡华, 王明, 罗锋. 基于直升机航空重力同步地形的布格改正处理[J]. 物探与化探, 2023, 47(2): 447-457 doi:10.11720/wtyht.2023.1289

QU Jin-Hong, JIANG Zuo-Xi, ZHOU Xi-Hua, WANG Ming, LUO Feng. Airborne Bouguer gravity based on synchronous terrains surveyed using helicopter airborne gravimetry[J]. Geophysical and Geochemical Exploration, 2023, 47(2): 447-457 doi:10.11720/wtyht.2023.1289

0 引言

20世纪90年代初期至今,随着差分全球定位技术(DGNSS)的成熟,航空重力仪及测量技术才得到迅速发展^[1-2]。航空重力测量以飞机为载体,融合了重力传感器、惯性系统(INS)和DGNSS等技术,获取近地空中重力加速度的一种动态重力测量方法^[3⇓⇓-6]。航空重力测量数据进行多项处理后才能更好反映地下密度分布的重力异常,为重力反演和后期应用做好准备。布格改正利用高精度数字高程模型(DEM)进行地形改正和中间层改正后,把重力异常归算到大地水准面上,是数据处理中的重要环节。因此,获取精准的地形高程是提升布格重力的改正质量的关键。

航空重力布格改正中,一般使用1:25万或更大比例尺的数字高程模型 ^[1],对于大部分测区都能满足改正需求。但在重点勘探区内,多处大型新、老矿场的大规模采矿活动从未间断过,区内存在多处采空区、排土场和尾矿库等;又随着城镇化建设,区内的居民住宅、商业高楼拔地而起,这些因素在不同程度上改变和重塑着地质形态,像人类开发活动频繁、地表高程破坏严重的测区,若仍依靠传统搜集数字地形的方式,则会由其制作年代久远、地形高程改变速度太快或地形数据更新滞后等原因,使搜集的地形数据无法与航空重力测量数据进行同步匹配,贸然使用会带来极大的改正误差。

本文使用加大量程后的俄罗斯GT-2A航空重力仪,其抗颠簸能力比GT-1A得到增强^[7-8]。国内首次集成了直升机重磁测量系统,并采用离地200 m高度随地形起伏飞行,在重点勘查实验区开展直升机航空重磁测量。系统搭载了DGNSS系统、单点GNSS定位导航系统和TRA 3000无线电雷达高度计等测高设备,通过机载GNSS飞行高度与无线电离地高度进行求差,再进一步处理后获得同步实测地形。使用实测地形进行航空重力布格改正后,矿山周边因地形不匹配造成布格重力假异常的现象被消除,处理结果获得明显提升。

1 实验区概况与地形数据处理

1.1 实验区地形概况

实验区位于鞍山—本溪整装铁矿勘查区,该区属我国重点勘探地区,已知东西鞍山、齐大山等多个特大型铁矿,其分布范围广、规模大、矿体与围岩之间具有明显的密度差。测区中心位置为鞍山市,测区东南高、西北低,东南部为山区,最高峰位于测区中南部海拔520 m。西北部为低缓平原地带,一般高度在40~80 m。区内东西鞍山、齐大山、大孤山、小岭子和眼前山多处开采的铁矿区等在不断形变中,并且城市高层建筑也在陆续升起。

为验证多个不同时期的数字地形对实验区航空重力布格改正的影响,本文搜集了国家地理信息局的1:25万、1:5万DEM和3种全球典型的免费开放DEM数据(ASTER、SRTM和AW3D30),后3种数据的空间分辨率均为30 m,基本信息见表1。ASTER GDEM数据采用2019年发布的V3版产品,是世界上最先免费发布的全球30 m尺度的DEM数据,数据精度检验:在日本区域高程精度为12.6 m。SRTM DEM属于雷达产品,平面精度20 m,高程标称精度16 m,实际精度约9 m^[9],于2000年由美国“奋进”号航天飞机采集,SRTM数据按精度可以分为SRTM1和SRTM3,对应的分辨率分别为30 m和90 m。AW3D30 DEM由日本宇宙航空研究机构(JAXA)研制,它源自ALOS卫星搭载的全色遥感立体测绘仪(PRISM)采集了300万个场景的光学立体像对数据,首先生成全球5 m的数字地表模型(DSM),平均精度为3.4 m,并以此重采成30 m尺度的数据于2015年5月免费发布,高程精度为5 m^[10],实际精度约4.4 m,被称为30 m尺度上精度最高的全球免费DEM产品,并覆盖全球所有的土地尺度。

表1 全球公开版30 m分辨率DEM基本参数

Table 1 Basic parameters of the global public version of 30 m resolution DEM

	ASTER	SRTM1	AW3D30
水平基准	WGS84	WGS84	GRS80
高程基准	EGM96	EGM96	EGM96
空间分辨率/m	30	30	30
高程精度/m	12.6	9	4.4
覆盖范围	83°N~83°S	60°N~56°S	84°N~84°S
采集技术	立体像对	InSAR	立体像对
采集时间/年	1999~2008	2000	2006~2011
使用版本	V3	V3	V2.2

新窗口打开| 下载CSV

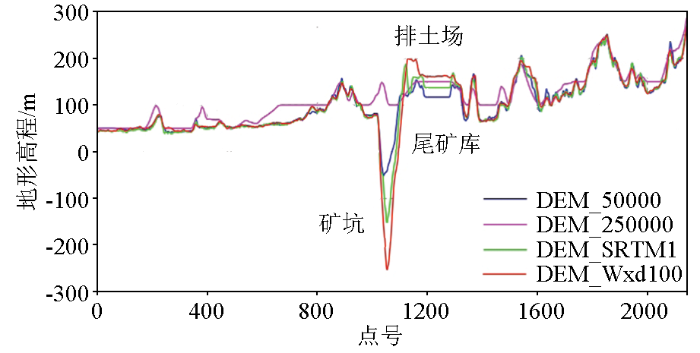
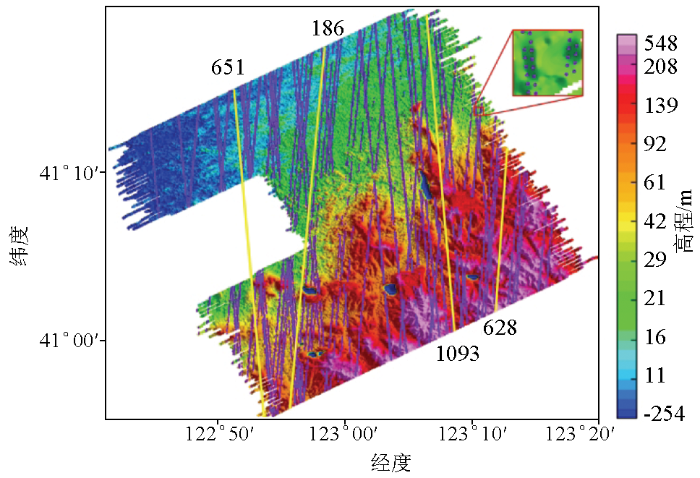
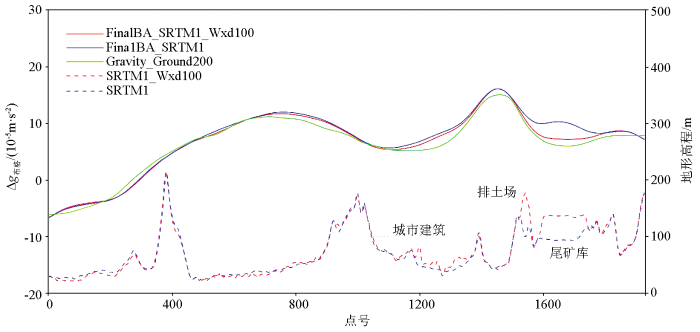
图1为经过大孤山矿坑的测线L1710上部分搜集的DEM数据与实测地形的对比,图中可以看出1:25万数据存在多处阈值设置,分辨率和精度都比较差,实验中排除此项数据。1:5万数据具有25 m的最好分辨率,但从矿坑开采程度推测数据制作时间应早于2000年2月份采集的SRTM1。而L1710的Wxd100实测地形为直升机航空重磁勘查系统同步获取,它的作业时间为2013年12月。从1:5万、SRTM1和Wxd100数据中,可以观察到矿坑不断加深和排土场、尾矿库不断垒高的动态变化。鉴于地表形态在不同时期改变较大的情况,搜集滞后的数字地形进行布格改正显然变得不合理。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 测线L1710上部分搜集DEM数据与实测地形对比

Fig.1 Comparison of DEM data collected on survey line L1710 with actual topography

本文制作的实验区地形参考椭球参数为WGS84,高程基准采用EGM96模型。其中1:5万的DEM采用2000国家坐标系,采用1985国家高程基准;AW3D30的参考椭球为GRS80。在计算前,不同数据之间首先统一不同的参考椭球和高程基准,有文献表明这3种不同的椭球参数之间参考系差异极小,同一点的定位精度优于1 mm^[11];而1985高程基准面与全球高程基准的差异大概在21~46 cm之间^{[12⇓⇓-15]}。

1.2 实测地形数据制作

1.2.1 实测地形测量原理

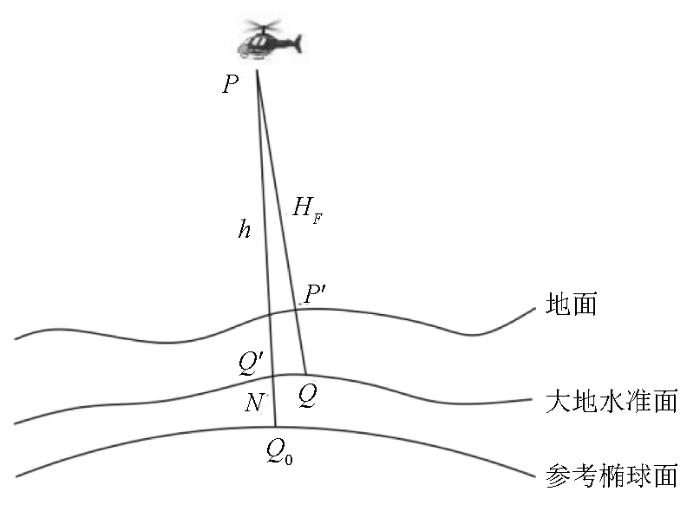
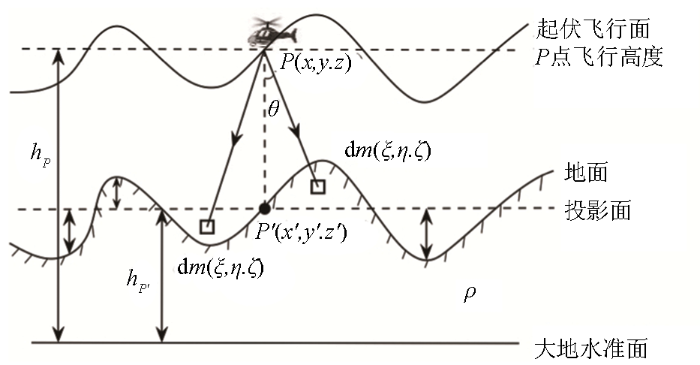
无线电雷达高度计作为指导飞机保持一定离地高度飞行的一种辅助设备,经常使用在航空物探低空起伏飞行中。它测得的是飞机离地面的高度,称为净空高度H_F,它与正高H、大地高h、地形高H_T及大地高到正高的改正值N之间的关系,如图2所示。P为测线上的一点,PP'=H_F,PQ=H,P'Q=H_T,PQ₀=h,Q'Q₀=N,若忽略垂线偏差的影响,几何关系如下:

(1)

H = H_{F} + H_{T} = h - N

(2)

H_{T} = h - N - H_{F}

。

式(2)表明,若测得飞机的GNSS大地高和离地净空高度,可获得飞机测点下方对应的地形高数据。然而,航空重力测量主要用于测定地面作业困难地区的地球重力场^[16],而部分区域的DEM往往更新程度不够,难以实际应用。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 高程之间的相互关系

Fig.2 Relationship between elevations

1.2.2 实测地形处理与实现

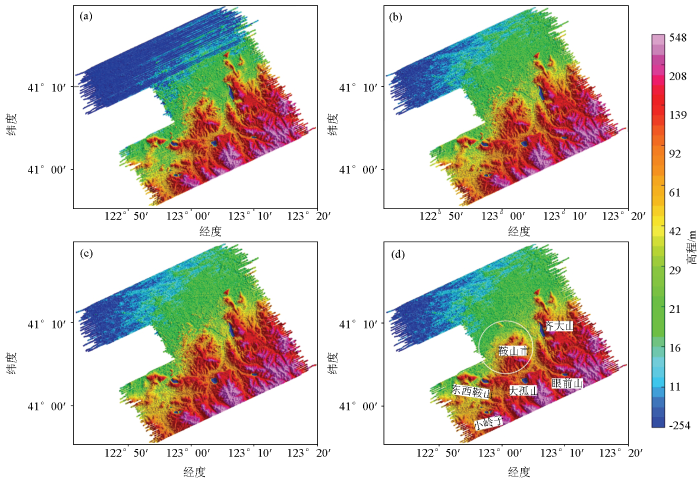
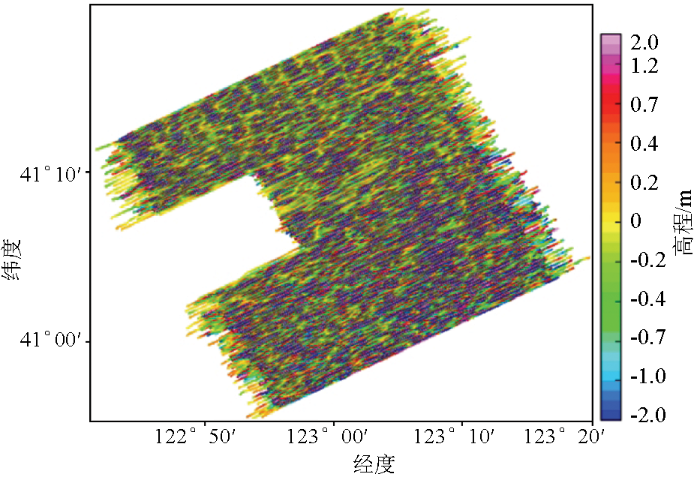
根据上述测量原理,首先从正、反方向重复测线的错位地形曲线中确定无线电高度数据的滞后时间,进行滞后校正后获得初步实测地形,见图3a。图中存在着明显的水平条带差异,与航空地球物理勘探中的航空磁法、航空重力等情况不尽相同,但均表现为一系列沿测线方向的条带状干扰,采用航空地球物理中常用的切割线调平和微调平方法,并设置适宜的调平参数,可以处理条带干扰问题。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 实测地形处理过程

a— 初步实测地形;b—切割线调平后实测地形;c—微调平后实测地形;d—剥离城市高楼后实测地形

Fig.3 Actual surveyed terrain processing

a—initially obtain the actual surveyed terrain; b—actual surveyed terrain is levelled by the tie-line; c—actual surveyed terrain is levelled by microlevelling process; d—actual surveyed terrain after stripping off tall buildings

为此在测线方向布置一定量的切割线,通过测线与切割线交叉点处的差值调整测线间水平差异,广泛使用的是切割线调平^[17⇓-19],此处通过交叉点对切割线进行1阶斜改后再对测线调平,如图3b所示。切割线调平主要用于水平差异较大的数据调整,调平后仍存在一定的残留水平差,还需进一步采取微调平^[20-21]。微调平采用频率域与空间域组合滤波,相对于切割线调平,微调平处理更为灵活,对数据的理解和经验性成分较多。Ferraccioli等^[21]介绍了Oasis Montaj中采用的滤波器,从网格数据中采用余弦方向滤波加高通巴特沃斯滤波器分离出条带干扰,公式如下:

(3)

D (θ) = 1 - {[c o s (α - θ + π / 2)]}^{n}

(4)

B (k) = 1 - \frac{1}{1 + {(k / k_{0})}^{n}}

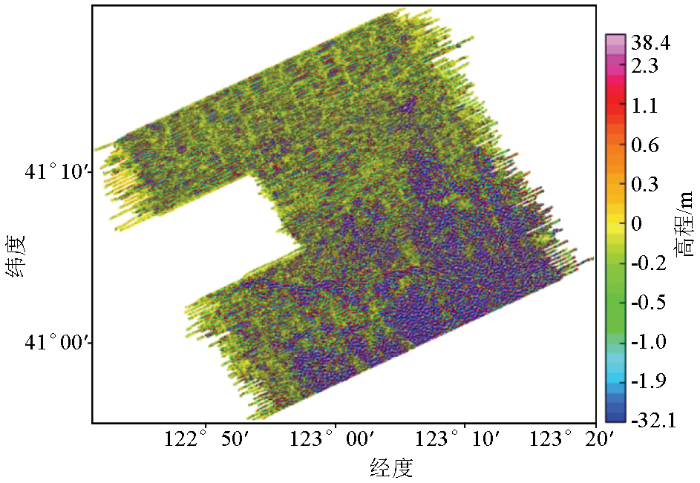
其中:式(3)是频率域α方向上n阶方向滤波器;式(4)是n阶高通巴特沃斯滤波器;θ、k分别是圆波数和波数;k₀对应高通滤波的波数。α应选择沿测线方向,通常方向滤波器阶数取2,巴特沃斯滤波器阶数取6,波长为4~10倍测线间距(此处设置4,数据质量越差参数依次增大)。按照上述滤波器组合提取图3b中的剩余条带,图4则为提取的残留水平差,可以看出提取的并非只有条带干扰,还包含大量的低幅高频DEM信息,与图3b的DEM轮廓基本一致。由于噪声干扰和DEM信息所处的频带通过频率域滤波不可能彻底分离,还需进一步提取和分离条带干扰。此处使用Naudy等提出的非线性滤波处理方法^[22],其中Naudy滤波长度为测线间距的5倍,高程幅值的滤波阈值设为2 m,如图5所示已剔除DEM高程轮廓信息的条带干扰,也可以通过多项式拟合、样条插值和中值滤波等方法处理^[23]。经过一次微调平后,测线间尚残存少量的水平差,可重复上述过程直至获得合理的结果,如图3c。由于微调平处理并不针对特定航空地球物理资料,条带干扰不管是飞行高度差异还是仪器等其他因素引起,方法本身均适用。

通过无线电高度计测量获取的是地表高程,城市高楼和高大植被等地表信息也都包含在实测地形中,这些信息也会影响到地形改正。因此,参考多个不同时期的高分辨率DEM数据,以早期1:5万DEM和SRTM1数据为主,对鞍山市区超过20 m以上的小高层、高层建筑进行替换或剥离,如图3d所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 提取的条带干扰

Fig.4 Extracted striping patterns

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 Naudy非线性滤波提取条带干扰

Fig.5 Extracted striping patterns by Naudy non-linear filter

从图6中看出5种不同时期的地形数据所对应的矿场开采程度也不尽相同。在获得实测地形后为满足地形改正的范围要求,需要与测区外围DEM数据进行网格缝合。图6f为实测地形与SRTM1外围数据缝合后的地形数据,白色线框为缝合边界,5处矿场和鞍山市区也在其中。

图6

新窗口打开| 下载原图ZIP| 生成PPT

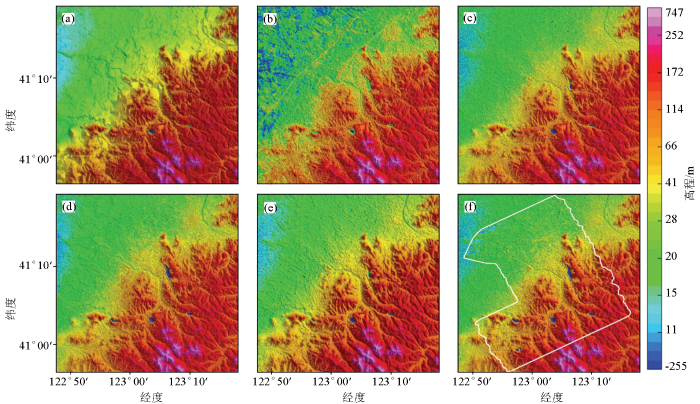
图6 多源DEM数据与缝合SRTM1后的实测地形数据

a—1:5万地形数据;b—ASTER数据;c—SRTM1数据;d—AW3D30数据;e—SRTM3数据;f—实测地形与SRTM1缝合

Fig.6 Multi-source DEM data and the actual surveyed terrain after stitching SRTM1

a— 1:50000DEM; b—ASTER; c—SRTM1; d—AW3D30; e—SRTM3; f—actual surveyed terrain was stitched with SRTM1

1.3 地形数据精度评价

1.3.1 实测地形测量分项评价

实测地形由飞行GNSS大地高与无线电离地高度求差后获得,其误差主要来自于这两者的测量误差^[24]。航空重力测量系统采用Ashtech Z-Xtrime的DGNSS移动站(移动站同时为机载导航定位系统和航磁数据定位提供GNSS信号)和Z-Max的DGNSS地面基站组成差分全球定位系统,差分定位结果则用于航空重力中垂直加速度误差改正和航重数据定位。在开工和飞行期间,分别对地面基站和移动站进行了3次单点GNSS和2次DGNSS的定位静态测试,观测时间均在2 h以上,观测统计静态单点GNSS高度误差在2~5 m,静态DGNSS高度误差在0.02 m之内,见表2。

表2 定位静态观测标准差(STD)统计

Table 2 Static measurement standard deviation (STD)

	序号	东向距/m	北向距/m	高度/m	水平面/m
单点GNSS基站	1	0.699	0.995	2.315	1.216
	2	0.599	1.395	2.632	1.519
	3	0.565	1.390	2.366	1.500
单点GNSS移动站	1	1.292	2.817	4.839	3.099
	2	1.071	2.241	3.268	2.484
	3	1.061	1.817	3.456	2.104
DGNSS移动站	1	0.010	0.007	0.006	0.012
DGNSS移动站	2	0.002	0.003	0.006	0.003

新窗口打开| 下载CSV

雷达高度计作为一种成熟的传感器在航空领域已经有70多年的应用历史,是通过无线电波的反射来测量高度的设备,它由发射、接收装置组成。本文测量系统中搭载美国Trimble公司TRA-3000雷达高度计,根据离地200 m起伏飞行高度,由说明书提供的7%离地误差公式推算,测量精度小于14 m。

1.3.2 实测地形动态测量评价

Wxd100实测地形从航磁测网中提取的测线间距为100 m,飞行高度由GNSS单点定位提供;而Wxd400从航重测网提取的测线间距为400 m,飞行高度由DGNSS差分定位提供。航空重复线测量常用于评估仪器动态测量的实际精度及仪器稳定性的一种测试方法,也适用于地形数据的重复线精度评价。图7中,从航空重力仪重复线动态精度测试中提取出一组重复地形数据,在大地高400 m平飞下,地形相对变化约170 m,对地形重复线的质量评价采用内符合统计^[25]。地形重复线的均方根差(RMSE)为2.55 m,经内符合水平调整后RMSE为2.53 m。

图7

新窗口打开| 下载原图ZIP| 生成PPT

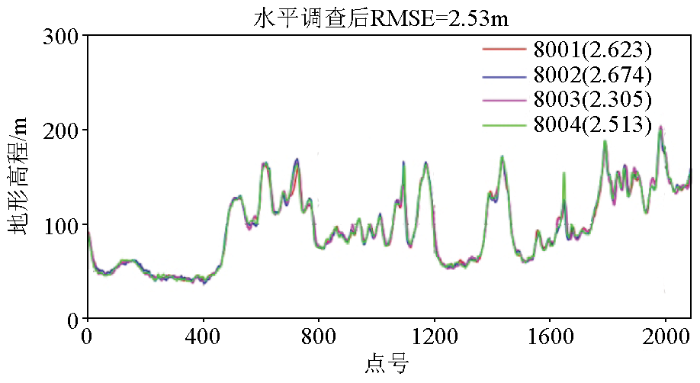
图7 地形高程重复线内符合精度统计

Fig.7 Internal accuracy statistics for repeated lines of elevation

Wxd100和Wxd400实测地形中都布设了测线和控制切割线^[26],通过对调平前的测网交叉点进行质量评价,可以评价实测地形的区域性高程精度,见表3。表中Min为最小值、Max为最大值、ME为平均误差、STD为标准差、RMSE为均方根差(视切割线为真值);表中交叉点总精度计算方法采用航空物探技术规范的统计方法,将所有交叉点的差值平方和除以2倍的交叉点数后再开平方^[27]。

表3 实测地形中测网交叉点统计

Table 3 Statistics of survey network intersections of actual surveyed terrain

	Wxd400	Wxd100
交叉点/个	609	4762
Min/m	-33.15	-91.7
Max/m	67.75	98.6
ME/m	0.03	0.61
STD/m	5.71	7.97
RMSE/m	5.71	7.99
总精度/m	4.04	5.65

新窗口打开| 下载CSV

1.3.3 基于ICESat-2/ATLAS下的高程精度评价

ICESat-2/ATLAS是目前高程精度最高的星载激光数据,能够作为生产高精度全球地面参考高程的基础数据。2018年9月,美国国家航空航天局(NASA)发射了ICESat-2卫星,其搭载的激光载荷——先进地形激光测高系统(ATLAS),相比ICESat-1/GLAS具有更高的精度和更小的激光足印,足印直径约为17 m,沿轨足印间距0.7 m,采用6波束激光对地面探测,每两束强、弱一组,两束相间90 m,每组相间约3.3 km^[28]。强弱光束形成交叉测量,能够有效提高对坡度和地表高程变化的检测能力^[29],高程精度由1代的15 cm提升到10 cm,完全满足对搜集的多源DEM数据和实测地形高程精度评价的需求。

本文使用2021年4月发布的ICESat-2/ATL08高程V4版本,存储了陆地高程和冠层高度数据,覆盖范围为全球,下载网站 https://nsidc.org/data/atl08/versions/4。ATL08数据在实验区内分布了4条轨道:186、628、651和1093,采集时间从2019年1月~2021年1月。每条轨道在此时间段内扫描8~10次左右,每次扫描生成6束激光,而且扫描轨迹与上一次比较都在轨道附近发生一定的偏移,如图8所示紫色激光束分布在实验区的各个角落。并剔除了部分信号弱的光子、实验区内数据极少和无数据的激光束。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 轨道上ATL08激光数据在实验区分布

Fig.8 Map of ATL08 Laser data on the track in the experimental area

从激光束中提取ATL08高程后,分别与Wxd100、Wxd400、1:5万DEM和免费开放的DEM数据(SRTM1、AW3D30、ASTER和SRTM3)进行高程精度统计。ICESat-2测高数据的精度与成像时间、坡度、地表覆盖、信噪比等因素有关,其中高程精度随坡度的上升而显著下降;夜晚观测数据的高程精度高于白天;裸地的高程精度高于植被覆盖的区域,植被覆盖率越高,高程精度越低^[30]。表4中调整前的统计结果,则保留了矿场周边和城市区域的ATL08数据,Wxd100表明实测数据质量确实好于所有收集的数据。为进一步验证实测数据与其余DEM的质量水平,剔除了形变大的区域和含有跳点的ATL08数据,保留率约87%;调整后统计Wxd100的高程精度(RMSE)好于ASTER,略低于其他DEM;Wxd400的高程精度与ASTER相当,低于其他DEM。

表4 基于ICESat-2/ATL08下的多源DEM数据统计

Table 4 Multi-source DEM data statistics based on ICESat-2/ATL08

		Wxd100	Wxd400	SRTM1	AW3D30	ASTER	1:5万	SRTM3
调整前	点数/个	22162	20456	22745	22745	22745	22745	22745
	Min/m	-116.87	-111.62	-125.98	-123.49	-125.37	-142.56	-123.73
	Max/m	149.7	149.24	230.99	228.2	226.68	284.35	229.89
	ME/m	1.54	2.42	-0.75	2.1	-4.2	-0.46	-0.31
	STD/m	9.79	12.33	14.88	11.24	14.59	17.86	14.92
	RMSE/m	9.91	12.56	14.90	11.43	15.18	17.87	14.93
调整后	点数/个	19279	17720	19848	19848	19848	19848	19848
	Min/m	-27.13	-83.83	-24.84	-21.56	-55.45	-38.24	-27.56
	Max/m	44.9	80.03	37.94	49.86	39.72	53.54	35.72
	ME/m	1.37	2.4	-0.51	2.08	-4.09	-0.05	-0.06
	STD/m	5.15	8.60	3.66	3.78	7.84	4.39	4.07
	RMSE/m	5.33	8.93	3.69	4.31	8.84	4.39	4.07
	采集时间	2013.10~2014.1	2013.12~2014.1	2000.2	2006~2011	1999~2008	不详	2000.2

新窗口打开| 下载CSV

又经过地形分类,分别对平原、丘陵山区的区域进行了精度统计。表5表明,两个实测地形的平原地区精度好于3 m,远优于ASTER,与其他DEM精度相当;而实测地形的丘陵、山区地带的精度下降程度高于其他DEM。在丘陵、山区中,SRTM1<SRTM3<AW3D30<1:5万DEM,精度依次降低,但相差不大;Wxd100的高程精度略低于前4种地形数据,Wxd400的高程精度稍差于ASTER。

表5 基于ICESat-2/ATL08下的多源DEM数据分区统计

Table 5 Multi-source DEM data partition statistics based on ICESat-2/ATL08

		Wxd100	Wxd400	SRTM1	AW3D30	ASTER	1:5万	SRTM3
丘陵及山区	点数/个	9894	9048	10220	10220	10220	10220	10220
	Min/m	-27.13	-83.83	-24.84	-21.56	-55.45	-38.24	-27.56
	Max/m	44.9	80.03	37.94	49.86	38.37	53.54	35.72
	ME/m	2.48	3.62	0.3	2.61	-6.71	1.33	0.8
	STD/m	6.71	11.74	4.75	4.83	8.35	5.69	5.40
	RMSE/m	7.15	12.28	4.76	5.49	10.71	5.84	5.46
平原	点数/个	9313	8613	9547	9547	9547	9547	9547
	Min/m	-10.45	-15.84	-14.84	-9.24	-25.31	-15.87	-14.98
	Max/m	35.01	49.27	16.46	46.54	39.72	20.52	17.1
	ME/m	0.21	1.13	-1.35	1.54	-1.21	-1.49	-0.96
	STD/m	2.14	2.23	1.52	2.07	6.08	1.20	1.29
	RMSE/m	2.15	2.50	2.03	2.57	6.20	1.91	1.60

新窗口打开| 下载CSV

2 航空布格重力改正及评价方法

2.1 航空重力地形改正原理

以航空重力飞行测点P为观测点,垂直地面投影测点P'的水平面内,如图9所示,P'点周围任一不在投影面上的质量单元 $d m$ 对观测点P产生的重力异常采用方形域改正方法^[1]。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 航空重力地形改正示意

Fig.9 Schematic diagram of airborne gravity terrain correction

(5)

Δ g_{z} = G \int \frac{d m}{r^{2}} c o s θ = - G ρ ∭ \frac{ζ - z}{{[{(ξ - x)}^{2} + {(η - y)}^{2} + {(ζ - z)}^{2}]}^{3 / 2}} d ξ d η d ζ

其中G为万有引力常数;θ为P点与dm连线到Z轴的夹角, $c o s θ = - (ζ - z) / r$ ;r为dm到P点距离, $r = \sqrt{{(ξ - x)}^{2} + {(η - y)}^{2} + {(ζ - z)}^{2}}$ ; $d m = ρ d ξ d η d ζ$ ;ρ为密度。

上述公式计算复杂,一般采用近似积分的方法将投影测点P'为中心的四周地形再次分割成许多小块,计算出每一小块地形质量对测点P的重力改正值,然后累加求和便得到该点的地形改正值。

航空重力地形改正目前国内没有明确的要求,主要参考地面重力规范。本文使用加拿大商业地球物理软件Oasis Montaj地形改正模块处理,航空重力异常地形改正通常分为局部地形改正范围和区域地形改正范围,局部地改范围半径应在0~20 km,区域地改范围半径应在20~166.7 km之间不等,一般根据地形特点、任务要求选择最远半径 ^[31]。

2.2 航空布格重力计算

通过合并地形改正值和中间层改正值就获得布格重力改正值,采用直升机航空重力的波长分辨率(飞行速度除以2倍的滤波截止频率^[32])对改正值进行滤波,航空重力异常减去改正值就获得航空布格重力异常。中间层改正和航空布格重力的计算公式来自Oasis Montaj地改模块说明书:

(6)

\begin{array}{l} g_{s b} = 0.0419088 \cdot [ρ h_{s} + (ρ_{w} - ρ) h_{w} + (ρ_{i} - ρ_{w}) h_{i}] \end{array}

(7)

g_{b} = g - g_{s b} - g_{t}

其中,g_sb为布格改正值;ρ为岩石密度;ρ_w为水密度;ρ_i为冰密度;h_s为观测点到平均海平面的高度;h_w为水深(包括冰厚度);h_i为冰厚度;g_b为航空布格重力异常; g为航空重力异常值;g_t为地形改正值。

2.3 航空布格重力质量评价

2.3.1 航空布格重力外符合精度评价

利用已认可仪器测量出的物理场或由地面物探仪器测量数据向上延拓到同一测量高度上,与测线上航空重力场值进行对比,评价测线航空重力质量^[25]。具体做法:将某测线上测点的航空重力场值与其对应的地面标准场向上延拓到飞行高度后的差值,同时将测线对应标准场的水平均值作为基准去调整测线重力场的水平差,统计去水平后差值的均方根差,计算公式为:

(8)

R M S E = \pm \sqrt{{\frac{\overset{n}{\sum_{i = 1}} [(F_{i} - \bar{F} + \bar{P}) - P_{i}]}{n}}^{2}}

,
(

i

=1,2, …,

n

其中,n为测线与对应标准场的重复线公共段的测点数;F_i为测线上各测点的观测值;P_i为测线上各测点对应的标准场。 $\bar{F} = \overset{n}{\sum_{i = 1}} F_{i} / n$ 为测线的平均值, $\bar{P} = \overset{n}{\sum_{i = 1}} P_{i} / n$ 为测线对应标准场的平均值。

2.3.2 航空布格重力外符合总精度评价

上述外符合精度评价针对某条测线,而对所有测线或测区进行航空重力面积性外符合总精度评价,计算过程与式(8)类同,处理对象有所区别。其中,n为所有测线与对应标准场公共的测点数,F_i为所有测线上各测点的观测值,P_i为所有测线上各测点对应的标准场, $\bar{F} = \overset{n}{\sum_{i = 1}} F_{i} / n$ 为所有测线的平均值, $\bar{P} = \overset{n}{\sum_{i = 1}} P_{i} / n$ 为所有测线对应标准场的平均值。

3 实验结果与分析

本文使用了1:5万DEM、ASTER、SRTM1、AW3D30和SRTM3地形数据,分别设为A1~A5;制作的实测地形Wxd100与上述地形数据进行缝合后,分别设为B1~B5;Wxd400与SRTM1缝合设为B6。分别对这些地形数据展开航空重力布格改正,对地面1:5万大比例尺重力数据采用快速傅里叶变换(FFT)向上延拓至200 m飞行高度,并进行外符合评价。

表6中,A1~A5进行布格改正后的外符合精度,主要与原先地形质量和采集时间有关。与实测地形进行缝合后B1~B5,因实测地形仅改善了矿区周边和市区的局部区域,所以面积性的外符合总精度提升幅度不大。A5的分辨率比A3低,而对应的外符合总精度相当;缝合后的实测地形中B3与B6外符合总精度相差也不大。表7中,分别进行了地形之间的布格重力差值统计。结果表明A1与B1、A2与B2之间布格重力改善最明显,然后依次是A3与B3、A4与B4、A5与A3和B3与B6,均验证了上述观点,详见表7、图10。

表6 不同地形数据改正下的航空布格重力外符合总精度

Table 6 The total accuracy of external coincidence for airborne Bouguer gravity by different DEM data

序号	高程地形	分辨率/m	外符合总精度/ (10^-5m· ${s^{-}}^{2}$ )	采集时间
A1	1:5万	25	1.159	早于2000
A2	ASTER	30	1.305	1999~2008
A3	SRTM1	30	1.098	2000.2
A4	AW3D30	30	1.063	2006~2011
A5	SRTM3	90	1.097	2000.2
B1	1:5万_Wxd100	25	1.056	测区同步
B2	ASTER_Wxd100	30	1.090	测区同步
B3	SRTM1_Wxd100	30	1.054	测区同步
B4	AW3D30_Wxd100	30	1.057	测区同步
B5	SRTM3_Wxd100	90	1.056	测区同步
B6	SRTM1_Wxd400	30/80	1.059	测区同步

新窗口打开| 下载CSV

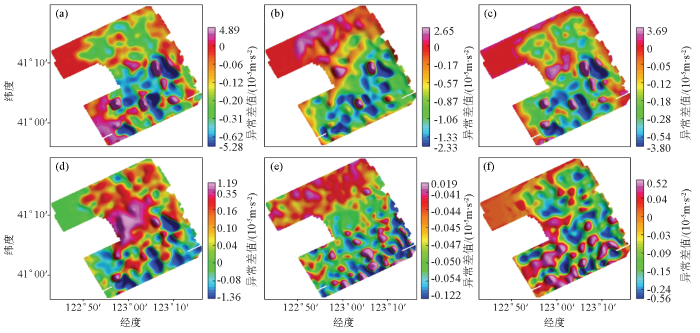
表7 对应地形之间的布格重力差值统计

Table 7 Statistics of Bouguer gravity difference between two DEM data

	B1~A1	B2~A2	B3~A3	B4~A4	B5~A5	A5~A3	B6~B3
Min/(10^-5m· ${s^{-}}^{2}$ )	-5.281	-2.329	-3.800	-1.356	-3.746	-0.122	-0.562
Max/(10^-5m· ${s^{-}}^{2}$ )	4.887	2.646	3.693	1.194	3.728	0.019	0.524
ME/(10^-5m· ${s^{-}}^{2}$ )	-0.206	-0.608	-0.201	0.063	-0.177	-0.048	-0.061
STD/(10^-5m· ${s^{-}}^{2}$ )	0.589	0.581	0.420	0.242	0.412	0.007	0.126

新窗口打开| 下载CSV

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 对应地形之间的布格重力异常差值

Fig.10 Difference map of Bouguer gravity anomaly difference between two DEM data

a—B1~A1; b—B2~A2; c— B3~A3;d—B4~A4;e—A5~A3; f— B6~B3

从实验区随机挑选出经过矿区的测线,统计了3个不同时期的地形和缝合实测地形后对应的布格重力外符合精度。表8表明,使用实测地形数据后,布格重力质量均有了明显的改善,部分测线质量的提升幅度很大。图11中,测线L2270展示了在实测地形SRTM1_Wxd100和SRTM1下,分别对应与地面向上延拓后的布格重力异常曲线,外符合精度从1.104×10^-5m/s²提升到0.673×10^-5m/s²,实测地形对排土场和尾矿库上方的布格重力有着较大的改善作用。

表8 典型测线在不同地形数据改正下的航空布格重力外符合精度

Table 8 The external coincidence accuracy of airborne Bouguer gravity under different DEM data for typical lines(10^-5m· ${s^{-}}^{2}$ )

线号	1:5万	SRTM1	AW3D30	1:5万_Wxd100	SRTM1_Wxd100	AW3D30_Wxd100	SRTM1_Wxd400	地形改变
L1990	0.801	0.669	0.645	0.649	0.646	0.650	0.680	排土场
L2070	1.077	0.863	0.811	0.785	0.786	0.786	0.800	矿坑、尾矿库
L2110	1.080	0.913	0.874	0.862	0.862	0.861	0.870	矿坑、尾矿库
L2230	1.126	0.915	0.677	0.644	0.645	0.645	0.672	尾矿库、城市建筑
L2270	1.351	1.104	0.783	0.672	0.673	0.677	0.720	尾矿库、排土场
L2550	1.870	1.592	1.141	1.044	1.041	1.047	0.905	矿坑、排土场
L2590	1.849	1.565	1.059	0.947	0.945	0.951	0.933	矿坑、排土场
T9130	1.561	1.361	0.974	1.064	1.036	1.056	1.084	两处矿坑
T9140	1.699	1.308	0.747	0.672	0.672	0.676	0.665	排土场、尾矿库

新窗口打开| 下载CSV

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 测线L2270的航空布格重力异常对比

Fig.11 Comparison of airborne Bouguer gravity anomaly on L2270

4 结论

本文通过GNSS高度数据和雷达高度计获取地形数据,结合多源DEM数据进行质量评价后,并进行航空重力布格改正,得出以下结论:

1)采用GNSS高度数据和雷达高度计获取地形数据的方法,不仅作为航空重力测量中副产品没有额外成本,而且解决了航空重力地形改正中重力数据与地形数据同步匹配的难题。同时,对实测地形的调平处理中采用了Naudy非线性滤波分离了条带干扰,有效保留了低幅高频信息,提升了实测地形的高程精度。

2)实测地形的重复线内符合统计精度为2.53 m;Wxd100的测网交叉点的总精度为5.65 m,与基于高质量ICESat-2/ATL08下的RMSE为5.33 m较为接近;Wxd400的测网交叉点总精度为4.04 m,而基于激光数据下的RMSE为8.93 m,偏差较大的原因为Wxd400测线间距过稀网格插值所致。使用不同的评价方法有其适用性,评价结果较为可靠。

3)在实验区和丘陵、山区中实测地形精度,SRTM1<SRTM3<AW3D30<1:5万DEM<Wxd100,精度依次降低,分别为3.69、4.07、4.31、4.39、5.33 m和4.76、5.46、5.49、5.84、7.15 m,实测地形Wxd100的精度略低于前几种地形,但相差不大。SRTM3作为90 m分辨率地形数据的精度优于AW3D30和1:5万DEM,它们均可用于实测地形的外围数据中。而ASTER数据存在较多异常的高程值,对地形表达的准确性远不如前者们。

4)统计了地形数据1:5万DEM、ASTER、SRTM1、AW3D30和SRTM3,分别对应的航空布格重力外符合总精度,在高程精度相当的前提下,布格重力改正质量的高低与使用的地形数据生产时间离航空重力测量时间的远近有关。缝合实测地形Wxd100和Wxd400后,所有地形对应的布格重力质量都获得了一定的提升。SRTM3的分辨率比SRTM1降低了,但对应的布格重力质量没有降低。实测地形Wxd100和Wxd400在缝合SRTM1后,400 m测线距的实测地形对应的布格重力质量略低于前者。

5)本文使用实测地形进行航空重力地形改正和中间层改正后获得航空布格重力异常,采用向上延拓地面布格重力与全区和多条测线进行布格重力的外符合精度评价,验证了实测数据的可靠性。表明航空重力测量作业中同步获取地形数据用于布格改正的方法有效且实用,可以消除矿山周边布格重力的假异常现象。

6)航空重力布格改正的质量主要取决于地形数据的质量,而实测地形高程精度局限于雷达高度计的精度、测线间距设计等原因。将来搭载像机载激光雷达更高精度的测高设备时,势必会获取与航空重力数据同步的厘米级地形数据,可以大幅度地提升航空重力布格改正精度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

熊盛青, 周锡华, 郭志宏, 等.

航空重力勘探理论方法及应用[M]. 北京: 地质出版社, 2010.

[本文引用: 3]

Xiong

S Q

, Zhou

X H

, Guo

Z H

, et al.

Theory,method and application of the airborne gravity processing[M]. Beijing: Geological Publishing House, 2010.

[本文引用: 3]

[2]

William

R G

An historical review of airborne gravity

[J]. The Leading Edge, 1998(l):113-116.