|
|
|
| Research on edge depth inversion of 2D geological body based on gravity and magnetic field |
WANG Wan-Yin1,2,3,4( ), LUO Xin-Gang1,2,3,4,5( ), LUO Xin-Gang1,2,3,4,5( ) ) |
1. Institute of Gravity and Magnetic Technology, Chang'an University, Xi'an 710054, China
2. College of Geology Engineering and Geomatics, Chang'an University, Xi'an 710054, China
3. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education, Chang'an University, Xi'an 710054, China
4. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China
5. Department of Earth Sciences, Memorial University of Newfoundland, Newfoundland A1B3X5, Canada |
|
|
|
|
Abstract The edge depth of geological body plays a crucial role in the semi-quantitative interpretation of gravity and magnetic potential field exploration. At present, the main inversion methods of geological body edge depth mainly include Werner deconvolution method, analytical signal amplitude method, local wave number method, Tilt-depth method, Euler deconvolution method and curvature attribute inversion method. These methods all have problems of solution selection, stability and adaptability. This paper mainly studies the adaptability of different types of data and models. Through basic principle analysis and model test, the results show that Werner deconvolution method and Euler deconvolution method are applicable to the most types of data sources, followed by curvature attribute, and Tilt-depth is the least; Werner deconvolution method, Euler deconvolution method and curvature attribute methods can adapt to many models, the Tilt-depth is least. For gravity data, the analytical signal amplitude of the first vertical derivative as the data source is applicable to all methods. For magnetic data, the analytical signal amplitude as data source is applicable to all methods. At the same time, it is suggested that other scholars should follow the following principles when using these methods to invert the edge depth of the two-dimensional body: It is recommended that Werner deconvolution is preferred, followed by curvature attribute and Euler deconvolution. The gravity data source of Werner deconvolution method and Euler deconvolution method is recommended to use the horizontal derivative of the first vertical derivative, and the magnetic data source is recommended to use the horizontal derivative. The gravity data source of curvature attribute method is recommended to use the analytical signal amplitude of the first vertical derivative, and the magnetic data source is recommended to use the analytical signal amplitude. In addition, based on the above research conclusions, some suggestions on the future research directions of the solution screening, stability and adaptability of the edge depth inversion are given.
|
|
Received: 21 September 2022
Published: 05 July 2023
|
|
|
|
|
|
|
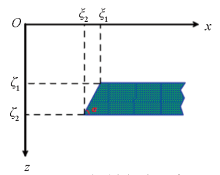
Schematic diagram of inclined step
|

| 输入数据类型 | | 重力 | VDR-HDR | VDR-VDR | VDR-ASA2 | VDR-k | | 磁力 | HDR | VDR | ASA2 | k |
|
Input data types of Werner deconvolution class methods
|
|
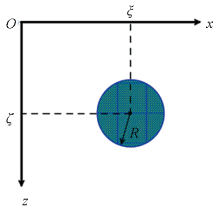
Diagram of horizontal cylinder
|

| 输入数据类型 | | 重力 | VDR-HDR | VDR-VDR | VDR-ASA | VDR-k | | 磁力 | HDR | VDR | ASA | k |
|
Input data types of the Euler deconvolution method
|

|
Werner deconvolution inverting edge depth of inclined step
a—magnetic anomaly; b—gravitational anomaly
|
|
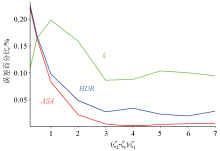
Relationship between the ratio of inclined step thickness and top buried depth and error
|

|
Tilt-depth inverting edge depth of inclined step
a—magnetic anomaly;b—gravitational anomaly
|

|
Euler deconvolution inverting edge depth of inclined step
a—magnetic anomaly; b—gravitational anomaly
|

|
Curvature attribute inverting edge depth of inclined step
a—magnetic anomaly; b—gravitational anomaly
|
|
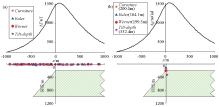
Inversion results of the inclined step from magnetic anomaly with noise
a—without filtering; b—filtering
|

|
Werner deconvolution inverting edge depth of parallelogram
a—magnetic anomaly; b—gravitational anomaly
|
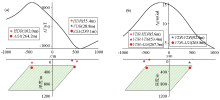
|
Tilt-depth inverting edge depth of parallelogram
a—magnetic anomaly; b—gravitational anomaly
|
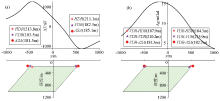
|
Euler deconvolution inverting edge depth of parallelogram
a—magnetic anomaly; b—gravitational anomaly
|
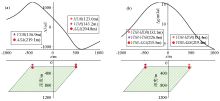
|
Curvature attribute inverting edge depth of parallelogram
a—magnetic anomaly; b—gravitational anomaly
|
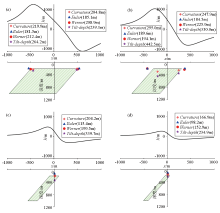
|
The edge depth inversion results of the variable-width parallelogram
a—parallelogram width:-500~500 m; b—parallelogram width:-300~300 m;c—parallelogram width:-100~100 m; d—parallelogram width:-50~50 m
|
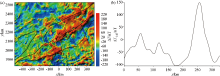
|
Magnetic anomaly of reduction to the pole in the Pearl River Mouth Basin
a—plan view; b—section view
|

|
Satellite altimetry gravity anomaly in the Pearl River Mouth Basin
a—plan view; b—section view
|

|
The edge depth inversion results in the Pearl River Mouth Basin
a—magnetic anomaly;b—gravity anomaly
|

| 反演深度/km | | 反演方法 | 第1个构造边缘 | 第2个构造边缘 | 第3个构造边缘 | 第4个构造边缘 | | 磁剖面 | 重力剖面 | 磁剖面 | 重力剖面 | 磁剖面 | 重力剖面 | 磁剖面 | 重力剖面 | | 沃纳反褶积 | 6.3 | 2.5 | 5.8 | 4.9 | 10.5 | 13.2 | 11.5 | 13.8 | | 曲率属性 | 7.2 | 4.5 | 6.1 | 5.9 | 12.3 | 14.1 | 11.5 | 15.9 | | 欧拉反褶积 | 2.7 | 9.6 | 0.4 | 0.6 | 9.7 | 3.3 | 5.1 | 16.5 | | Tilt-depth | 11.5 | | 11.3 | 12.1 | 17.9 | 35.5 | 22.7 | 14.8 |
|
The edge depth inversion results of thegravity and magnetic anomaly profile in the Pearl River Mouth Basin
|
| [39] |
鲁宝亮, 王万银, 赵志刚, 等. 南海深部构造特征及其地质意义:来自重磁位场反演的认识[J]. 地球物理学报, 2018, 61(10):4231-4241.
|
| [39] |
Lu B L, Wang W Y, Zhao Z G, et al. Characteristics of deep structure in the South China Sea and geological implications:Insights from gravity and magnetic inversion[J]. Chinese Journal of Geophysics, 2018, 61(10):4231-4241.
|
| [1] |
Salem A, Ravat D. A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data[J]. Geophysics, 2003, 68(6):1952-1961.

|
| [2] |
Salem A, Williams S, Fairhead D, et al. Interpretation of magnetic data using Tilt-angle derivatives[J]. Geophysics, 2008, 73(1):1-10.
|
| [3] |
Werner S. Interpretation of magnetic anomalies at sheet-like bodies[R]. Sveriges Geologiska Undersok.Ser.C,Arsbok 1953.
|
| [4] |
Hartman R R, Teskey D J, Friedberg J L. A system for rapid digital aeromagnetic interpretation[J]. Geophysics, 1971, 36(5):891-918.

|
| [5] |
Hansen R O, Simmonds M. Multiple-source Werner deconvolution[J]. Geophysics, 1993, 58(12):1792-1800.

|
| [6] |
Nabighian M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section its properties and use for automated anomaly interpretation[J]. Geophysics, 1972, 37(3):507-517.

|
| [7] |
Roest W R, Verhoef J, Pilkingto M. Magnetic interpretation using the 3D analytic signal[J]. Geophysics, 1992, 57(1):116-125.

|
| [8] |
胡中栋, 余钦范, 楼海. 三维解析信号法[J]. 物探化探计算技术, 1995, 17(3):36-42.
|
| [8] |
Hu Z D, Yu Q F, Lou H. 3D analytic signal method[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1995, 17(3):36-42.
|
| [9] |
Hsu S K, Sibuet J C, Shyu C T. High-resolution detection of geologic boundaries from potential-field anomalies:An enhanced analytic signal technique[J]. Geophysics, 1996, 61(2):373-386.

|
| [10] |
管志宁, 姚长利. 倾斜板体磁异常总梯度模反演方法[J]. 地球科学:中国地质大学学报, 1997, 22(1):81-85.
|
| [10] |
Guan Z N, Yao C L. Inversion of the total gradient modulus of magnetic anomaly due to dipping dike[J]. Earth Science:Journal of China University of Geosciences, 1997, 22(1):81-85.
|
| [11] |
Debeglia N, Corpel J. Automatic 3D interpretation of potential field data using analytic signal derivatives[J]. Geophysics, 1997, 62(1):87-96.

|
| [12] |
Bastani M, Pedersen L B. Automatic interpretation of magnetic dike parameters using the analytical signal technique[J]. Geophysics, 2001, 66(2):551-561.

|
| [13] |
张季生, 高锐, 李秋生, 等. 欧拉反褶积与解析信号相结合的位场反演方法[J]. 地球物理学报, 2011, 54(6):1634-1641.
|
| [13] |
Zhang J S. Gao R, Li Q S, et al. A combined Euler and analytic signal method for an inversion calculation of potential data[J]. Chinese Journal of Geophysics, 2011, 54(6):1634-1641
|
| [14] |
Thurston J B, Smith R S. Automatic conversion of magnetic data to depth,dip,and susceptibility contrast using the SPI (TM) method[J]. Geophysics, 1997, 62(3):807-813.

|
| [15] |
Phillips J D. Locating magnetic contacts:A comparison of the horizontal gradient,analytic signal,and local wavenumber methods[J]. Seg Technical Program Expanded Abstracts, 2000, 19(1):2484.
|
| [16] |
Pilkington M, Keating P. Contact mapping from gridded magnetic data—A comparison of techniques[J]. Exploration Geophysics, 2004, 35(4):306-311.

|
| [17] |
崔莉, 王万银. 局部波数在磁异常解释应用中的方法技术[J]. 物探与化探, 2011, 35(6):780-784.
|
| [17] |
Cui L, Wang W Y. The technique for application of local wavenumber to magnetic interpretation[J]. Geophysical and Geochemical Exploration, 2011, 35(6):780-784.
|
| [18] |
Miller H G, Singh V. Potential field tilt—A new concept for location of potential field sources[J]. Journal of Applied Geophysics, 1994, 32(2):213-217.

|
| [19] |
Verduzco B, Fairhead J D, Green C M, et al. The meter reader-New insights into magnetic derivatives for structural mapping[J]. Leading Edge, 2004, 23(2):116-119.

|
| [20] |
Salem A, Williams S, Fairhead J D, et al. Tilt-depth method:A simple depth estimation method using first-order magnetic derivatives[J]. Leading Edge, 2007, 26(12):1502-1505.

|
| [21] |
Thompson D T. Euldph—A new technique for making depth estimates from magnetic data[J]. Geophysics, 1982, 47(1):31-37.

|
| [22] |
Reid A B, Allsop J M, Granser H, et al. Magnetic interpretation in three dimensions using Euler deconvolution[J]. Geophysics, 1990, 55(1):80-91.

|
| [23] |
Marson I, Klingele E E. Advantages of using the vertical gradient of gravity for 3D interpretation[J]. Geophysics, 1993, 58(11):1588-1595.

|
| [24] |
Keating P B. Weighted Euler deconvolution of gravity data[J]. Geophysics, 1998, 63(5)1595-1603.

|
| [25] |
Mushayandebvu M F, Driel P V, Reid A B, et al. Magnetic source parameters of two-dimensional structures using extended Euler deconvolution[J]. Geophysics, 2001, 66(3):814-823.

|
| [26] |
史辉, 刘天佑, Ghaboush D M. 利用欧拉反褶积法估计二度磁性体深度与位置[J]. 物探与化探, 2005, 29(3):230-233.
|
| [26] |
Shi H, Liu T Y, Ghaboush D M. The application of Euler deconvolution to estimating depth and location of the 2D magnetic body[J]. Geophysical and Geochemical Exploration, 2005, 29(3):230-233.
|
| [27] |
Florio G, Fedi M, Pasteka R. On the application of Euler deconvolution to the analytic signal[J]. Geophysics, 2006, 71(6):L87-L93.

|
| [28] |
鲁宝亮, 范美宁, 张原庆. 欧拉反褶积中构造指数的计算与优化选取[J]. 地球物理学进展, 2009, 24(3):1027-1031.
|
| [28] |
Lu B L, Fan M N, Zhang Y Q. The calculation and optimization of structure index in Euler deconvolution[J]. Progress in Geophysics, 2009, 24(3):1027-1031.
|
| [29] |
Hansen R O, Deridder E. Linear feature analysis for aeromagnetic data[J]. Geophysics, 2006, 71(6):L61-L67.

|
| [30] |
Phillips J D, Hansen R O, Blakely R J. The use of curvature in potential-field interpretation[J]. Exploration Geophysics, 2007, 38(2):111-119.

|
| [31] |
刘金兰. 重磁位场新技术与山西断陷盆地构造识别划分研究[M]. 西安: 长安大学, 2008.
|
| [31] |
Liu J L. Development new technologies for potential field processing and research on the tectonic recognition division of Shanxi fault basin[D]. Xi'an: Chang'an University, 2008.
|
| [32] |
Roberts A. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 2001, 19(2):85-100.

|
| [33] |
王万银. 位场边缘识别方法技术研究[D]. 西安: 长安大学, 2009.
|
| [33] |
Wang W Y. The research on the edge recognition methods and techniques for potential field[D]. Xi'an: Chang'an University, 2009.
|
| [34] |
范美宁. 欧拉反褶积方法的研究及应用[D]. 长春: 吉林大学, 2006.
|
| [34] |
Fan M N. The study and application of Euler deconvolution method[D]. Changchun: Jilin University, 2006.
|
| [35] |
Wang W Y, Pan Y, Qiu Z Y. A new edge recognition technology based on the normalized vertical derivative of the total horizontal derivative for potential field data[J]. Applied Geophysics, 2009, 6(3):226-233.

|
| [36] |
何涛, 王万银, 黄金明, 等. 正则化方法在比值类位场边缘识别方法中的研究[J]. 物探与化探, 2019, 43(2):308-319.
|
| [36] |
He T, Wang W Y, Huang J M, et al. The research of the regularization method in the ratio methods of edge recognition by potential field[J]. Geophysical and Geochemical Exploration, 2019, 43(2):308-319.
|
| [37] |
Zhu Y J, Wang W Y, Farquharson C G, et al. Normalized vertical derivatives in the edge enhancement of maximum-edge-recognition methods in potential fields[J]. Geophysics, 2021, 86(4):G23-G34.

|
| [38] |
罗新刚, 王万银, 张功成, 等. 基于重力资料的南海及邻区断裂分布特征研究[J]. 地球物理学报, 2018, 61(10):4255-4268.
|
| [38] |
Luo X G, Wang W Y, Zhang G C, et al. Study on distribution features of faults based on gravity data in the South China Sea and its adjacent areas[J]. Chinese J.Geophys., 2018, 61(10):4255-4268.
|
| [1] |
SHAN Xi-Peng, XIE Ru-Kuan, LIANG Sheng-Jun, YU Xue-Zhong. An analysis of the influencing factors of helicopter TEM survey[J]. Geophysical and Geochemical Exploration, 2021, 45(1): 178-185. |
| [2] |
Xiao-Jing CHEN, Xin-Jun HU, Ning-Sheng LI, Bai-Zhou AN, Ya-Dong BAI. Research on the deep geological structure in Yinchuan Plain: 3D modeling based on geophysical data[J]. Geophysical and Geochemical Exploration, 2020, 44(2): 245-253. |
|
|
|
|

