|
|
|
| A modified interpolation-iteration method for gravity anomaly continuation from undulating surface to plane |
YANG Jing( ), GUO Liang-Hui( ), GUO Liang-Hui( ) ) |
| School of Geophysics and Information Technology, China University of Geosciences,Beijing 100083,China |
|
|
|
|
Abstract Gravity anomaly continuation from undulating surface to plane can provide gravity data on a flat horizontal plane for frequency-domain data processing and inversion. Based on the theory of conventional interpolation-iteration methods, this study proposed a modified interpolation-iteration method by introducing a correction factor of the undulating observation surface in the iteration and correction process. The improved method accelerated the iterative convergence speed and promoted the continuation effects. The theoretical model-based tests show that this method can be used to achieve stable and effective large-span gravity anomaly continuation from greatly undulating surface to plane. The continuation results presented by this method are better than those obtained using conventional interpolation-iteration methods. The application of Bouguer gravity anomaly data of the Sichuan-Yunnan region demonstrates that the modified interpolation-iteration method effectively enhanced anomalous signals and details and can provide reliable data for subsequent processing and interpretation.
|
|
Received: 22 July 2021
Published: 25 February 2022
|
|
|
|
Corresponding Authors:
GUO Liang-Hui
E-mail: 2010200015@cugb.edu.cn;guo_lianghui@163.com
|
|
|
|
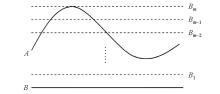
|
The diagram of interpolation-iteration method for gravity anomaly continuation from undulating surface to plane
|
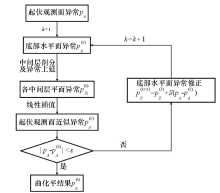
|
The workflow of the modified interpolation-iteration method
|

|
Undulating observation surface of theoretical model and its gravity anomaly
a—theoretical gravity anomaly at 0 m altitude;b—elevation of undulating observation surface;c—theoretical gravity anomaly at undulating observation surface
|
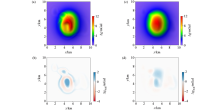
|
Comparison between the results of different interpolation-iteration methods and the gravity forward values of plane surface
a、b—the result of the routine interpolation-iteration method for continuation from undulating surface to plane and its deviation from the values of plane surface;c、d—the result of the modified interpolation-iteration method and its deviation from the values of plane surface
|

|
Different S comparison along profile A
|
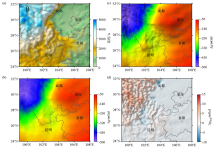
|
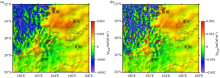
The Bouguer gravity comparison before and after continuation from undulating surface to plane of Sichuan-Yunnan region
a—the elevation of Sichuan-Yunnan region;b—the denoised Bouguer gravity anomaly;c—the Bouguer gravity anomaly after continuation from undulating surface to plane by using the modified interpolation-iteration method;d—the anomaly deviations before and after continuation from undulating surface to plane
|

|
The gravity anomaly comparison and the elevation along profile B
|
|
The vertical derivative of Bouguer gravity comparison before and after continuation from undulating surface to plane of Sichuan-Yunnan region
a—the vertical derivative of Bouguer gravity anomaly;b—the vertical derivative of Bouguer gravity
|
| [1] |
曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005.
|
| [1] |
Zeng H L. Gravity field and gravity exploration[M]. Beijing: Geological Publishing House, 2005.
|
| [2] |
Blakely R J. Potential theory in gravity and magnetic applications [M]. Cambridge: Cambridge University Press, 1995:316-320.
|
| [3] |
Guo L, Meng X, Chen Z, et al. Preferential filtering for gravity anomaly separation[J]. Computers & Geosciences, 2013,51:247-254.

|
| [4] |
Oldenburg D W. The inversion and interpretation of gravity anomalies[J]. Geophysics, 1974,39(4):526-536.

|
| [5] |
Cui Y, Guo L. A wavenumber-domain iterative approach for rapid 3-D imaging of gravity anomalies and gradients[J]. IEEE Access, 2019,7(1):34179-34188.

|
| [6] |
Pilkington M, Boulanger O. Potential field continuation between arbitrary surfaces-Comparing methods[J]. Geophysics, 2017,82(3):J9-J25.

|
| [7] |
Dampney C N G. The equivalent source technique[J]. Geophysics, 1969,34(1):39-53.

|
| [8] |
David A E. Equivalent sources used as an analytic base for processing total magnetic field profiles[J]. Geophysics, 1973,38(2):339-348.

|
| [9] |
Bhattacharyya B K, Chan K C. Reduction of magnetic and gravity data on an arbitrary surface acquired in a region of high topographic relief[J]. Geophysics, 1977,42(7):1411-1430.

|
| [10] |
Hansen R O, Miyazaki Y. Continuation of potential fields between arbitrary surfaces[J]. Geophysics, 1984,49(6):787-795.

|
| [11] |
Pilkington M, Urquhart W E S. Reduction of potential field data to a horizontal plane[J]. Geophysics, 1990,55(5):549-555.

|
| [12] |
Xia J, Sprowl D R, Adkins-Heljeson D. Correction of topographic distortions in potential-field data: A fast and accurate approach[J]. Geophysics, 1993,58(4):515-523.

|
| [13] |
Henderson R G, Cordell L. Reduction of unevenly spaced potential field data to a horizontal plane by means of finite harmonic series[J]. Geophysics, 1971,36(5):1046-1046.
|
| [14] |
Guspi F. Frequency-domain reduction of potential field measurements to a horizontal plane[J]. Geoexploration, 1987,24(2):87-98.

|
| [15] |
Pilkington M, Thurston J B. Draping corrections for aeromagnetic data: Line versus grid-based approaches[J]. Exploration Geophysics, 2001,32(2):95-101.

|
| [16] |
程振炎. 重磁场的有限元法曲化平[J]. 物探与化探, 1981,5(3):153-158.
|
| [16] |
Cheng Z Y. The finite element method of gravity and magnetic field[J]. Geophysical and Geochemical Exploration, 1981,5(3):153-158.
|
| [17] |
Xu S Z. The boundary element method in geophysics[M]. Tulsa: Society of Exploration Geophysicists, 2001:63-67.
|
| [18] |
Xu S Z, Yang C H, Dai S K, et al. A new method for continuation of 3D potential fields to a horizontal plane[J]. Geophysics, 2003,68(6):1917-1921.

|
| [19] |
徐世浙. 位场延拓的积分—迭代法[J]. 地球物理学报, 2006,49(4):1176-1182.
|
| [19] |
Xu S Z. The interpolation-iteration method for continuation of potential fields[J]. Chinese Journal of Geophysics, 2006,49(4):1176-1182.
|
| [20] |
刘东甲, 洪天求, 廖旭涛, 等. 位场曲化平积分方程的迭代解[J]. 地球物理学报, 2012,55(10):3467-3476.
|
| [20] |
Liu D J, Hong T Q, Liao X T, et al. Iterative solution of integral equation for potential field continuation from irregular surface to a horizontal plane[J]. Chinese Journal of Geophysics, 2012,55(10):3467-3476.
|
| [21] |
徐世浙, 余海龙. 位场曲化平的插值—迭代法[J]. 地球物理学报, 50(6):193-197.
|
| [21] |
Xu S Z, Yu H L. The interpolation-iteration method for potential fields continuation from undulating surface to plane[J]. Chinese Journal of Geophysics, 2007,50(6):193-197.
|
| [22] |
郭良辉, 孟小红, 石磊, 等. 优化滤波方法及其在中国大陆布格重力异常数据处理中的应用[J]. 地球物理学报, 2012,55(12):4078-4088.
|
| [22] |
Guo L H, Meng X H, Shi L, et al. Preferential filtering method and its application to Bouguer gravity anomaly of Chinese continent[J]. Chinese Journal of Geophysics, 2012,55(12):4078-4088.
|
| [1] |
YANG Rong-Xiang, WANG Wan-Yin, CAI Meng-Ke, WANG Ding-Ding, LUO Xin-Gang. A study of tectonic framework of the Qinnan sag in Bohai Basin and its adjacent areas based on satellite gravity anomalies[J]. Geophysical and Geochemical Exploration, 2023, 47(3): 584-596. |
| [2] |
WANG Run-Sheng, WU Bin, ZHANG Hai-Rui, YU Jia-Bin, DONG Yan-Long, GUO Guo-Qiang, KANG Yi-Ming. Gravity field characteristics and boundaries of geotectonic units on the northeastern margin of the Linyi uplift, Shandong Province[J]. Geophysical and Geochemical Exploration, 2023, 47(2): 279-289. |
|
|
|
|

