|
|
|
| Stretch correction method based on Curvelet sparse transform |
LIU Shi-You1( ), ZHANG Ming-Lin2, SONG Wei-Qi2 ), ZHANG Ming-Lin2, SONG Wei-Qi2 |
1. Hainan Branch of CNOOC (China) Co.,Ltd., Haikou 570311, China
2. School of Geosciences, China University of Petroleum (East China), Qingdao 266580, China |
|
|
|
|
Abstract NMO correction is an important step in seismic data processing, but it will produce the wavelet stretching distortion effect in the process of correction. With the increase of offset, the dominant frequency will decrease and the amplitude will increase.Due to stretch distortion, the in-phase axis is not leveled, leading to non-in-phase stacking, which will lead to frequency distortion and resolution decrease of horizontal stacking profile. Therefore, stretch correction is the key to improve the resolution of horizontal stacking profile.The stretching distortion of wavelet is incoherent in the curved sparse domain, and the stretching correction can be regarded as a nonlinear optimization process.By measuring the sparsity of the data in the sparse domain, a fast and effective algorithm is used to optimize the nonlinear problem generated by the wavelet stretching distortion, and finally the purpose of eliminating the wavelet stretching distortion is realized.The curved sparse transform stretching correction method can eliminate the wavelet stretching distortion caused by NMO correction, recover the high frequency information at the far offset and level the in-phase axis.Combining model data and actual data processing, the curved wave sparse stretch correction method can significantly improve the resolution of horizontal superposition profile.
|
|
Received: 15 June 2021
Published: 25 February 2022
|
|
|
|
|
|

| 层位 | 纵波速度vp
/(m·s-1) | 横波速度vs
/(m·s-1) | 密度ρ
/(g·cm-3) | | 1 | 3500 | 2500 | 2.0 | | 2 | 4000 | 3000 | 2.5 |
|
Model 1 layered media parameters
|
|
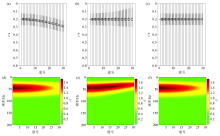
Test model 1
a—synthetic seismogram;b—conventional NMO correction results;c—curvelet sparse stretch correction;d—amplitude spectrum of the original seismic record;e—amplitude spectrum of NMO;f—amplitude spectrum of the tensile correction results by the method presented in this paper
|

| 层位 | 速度v/(m·s-1) | 密度ρ/(g·cm-3) | | 1 | 3500 | 1.3 | | 2 | 4000 | 1.5 | | 3 | 5000 | 2.0 | | 4 | 5500 | 2.2 |
|
Model 2 layered media parameters
|
|
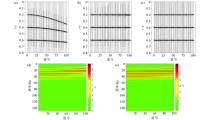
Test model 2(no random noise)
a—synthetic seismogram;b—conventional NMO correction results;c—curvelet sparse stretch correction;d—amplitude spectrum of NMO;e—amplitude spectrum of the tensile correction results by the method presented in this paper
|
|
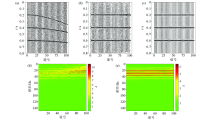
Test model 2(containing random noise)
a—synthetic seismogram;b—conventional NMO correction results;c—curvelet sparse stretch correction;d—amplitude spectrum of the original seismic record;e—amplitude spectrum of NMO;f—amplitude spectrum of the tensile correction results by the method presented in this paper
|

| 层位 | 速度v/(m·s-1) | 密度ρ/(g·cm-3) | | 1 | 4000 | 1.6 | | 2 | 6000 | 2.2 | | 3 | 5000 | 1.8 | | 4 | 5500 | 2.0 |
|
Model 3 layered media parameters
|
|
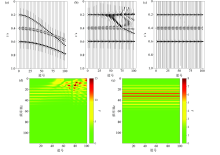
Test model 3
a—synthetic seismogram;b—conventional NMO correction results;c—curvelet sparse stretch correction;d—amplitude spectrum of NMO;e—amplitude spectrum of the tensile correction results by the method presented in this paper
|

|
Actual seismic data processing results
a—original CRP gathers;b—conventional NMO correction results;c—curvelet sparse stretch correction
|

|
Spectrum comparison before and after stretch correction
a—spectrum comparison between original CRP gathers and NMO correction results for long distance;b—spectrum comparison of original CRP gathers and curve sparse stretch correction results for long distance
|
|
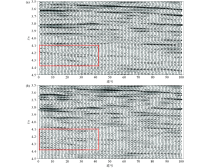
Stacked section
a—conventional NMO correction stack section;b—curvelet sparse stretch correction stack section
|
| [1] |
夏洪瑞, 葛川庆, 邹少峰. 动校拉伸现象分析及其消除[J]. 石油物探, 2005,44(3):220-224.
|
| [1] |
Xia H R, Ge C Q, Zou S F. Analysis and elimination of stretch phenomenon in dynamic school[J]. Geophysical Prospecting for Petroleum, 2005,44(3):220-224.
|
| [2] |
赵小龙, 吴国忱. 基于非稳态匹配的角度域叠前道集去调谐方法[J]. 物探与化探, 2017,41(1):141-146.
|
| [2] |
Zhao X L, Wu G C. Angle domain prestack gather detuning method based on unsteady matching[J]. Geophysical and Geochemical Exploration, 2017,41(1):141-146.
|
| [3] |
孙成禹, 谢俊法, 闫月锋. 一种无拉伸畸变的动校正方法[J]. 石油物探, 2016,55(5):664-673.
|
| [3] |
Sun C Y, Xie J F, Yan Y F. A dynamic correction method without stretching distortion[J]. Geophysical Prospecting for Petroleum, 2016,55(5):664-673.
|
| [4] |
Rupert G B, Chun J H. The block move sum normal moveout correction[J]. Geophysics, 1975,40(1):17-24.

|
| [5] |
Shatilo A, Aminzadeh F. Constant normal-moveout (CNMO) correction: a technique and test results[J]. Geophysical Prospecting, 2000: 48.
|
| [6] |
Hicks G J. Removing NMO stretch using the Radon and Fourier-Radon transforms[C]//63rd EAGE Conference & Exhibition, 2001.
|
| [7] |
Trickett S. Stretch-free stacking[C]//73rd Annual International Meeting,SEG,Expanded Abstracts, 1949: 4645.
|
| [8] |
崔宝文, 王维红. 频谱代换无拉伸动校正方法研究[J]. 地球物理学进展, 2007,22(3):960-965.
|
| [8] |
Cui B W, Wang W H. Study on spectrum substitution non stretching NMO method[J]. Progress in Geophysics, 2007,22(3):960-965.
|
| [9] |
Kazemi N, Siahkoohi H R. Local stretch zeroing NMO correction[J]. Geophysical Journal International, 2014,188(1):123-130.

|
| [10] |
Zhang B, Zhang K, Guo S, et al. Nonstretching NMO correction of prestack time-migrated gathers using a matching-pursuit algorithm[J]. Geophysics, 2013,78(1):U9-U18.

|
| [11] |
Abedi M M, Riahi M A. Nonhyperbolic stretch-free normal moveout correction[J]. Geophysics, 2016,81(6):U87-U95.

|
| [12] |
Zhang F, Lan N. Seismic gather wavelet stretching correction based on multi-wavelet decomposition algorithm[J]. Geophysics, 2020,85(5):1-33.

|
| [13] |
Barnes A E. Another look at NMO stretch[J]. Geophysics, 2012,57(5):749.

|
| [14] |
Buchholtz H. A note on signal distortion due to dynamic (NMO) corrections[J]. Geophysical Prospecting, 1972,20(2):395-402.

|
| [15] |
Candes E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Comm. Pure Appl. Math., 2005,59(8):1-15.

|
| [16] |
罗勇, 毛海波, 杨晓海, 等. 基于双重稀疏表示的地震资料随机噪声衰减方法[J]. 物探与化探, 2018,42(3):608-615.
|
| [16] |
Luo Y, Mao H B, Yang X H, et al. Random noise attenuation method for seismic data based on double sparse representation[J]. Geophysical and Geochemical Exploration, 2018,42(3):608-615.
|
| [17] |
Herrmann F J, Moghaddam P, Stolk C C. Sparsity- and continuity-promoting seismic image recovery with curvelet frames[J]. Applied & Computational Harmonic Analysis, 2008,24(2):150-173.
|
| [18] |
Gholami A. Residual statics estimation by sparsity maximization[J]. Geophysics, 2013,78(1):V11-V19.

|
| [19] |
Gholami A, Hosseini S M. A general framework for sparsity based denoising and inversion[J]. IEEE Transactions on Signal Processing, 2011,59(11):5202-5211.

|
| [1] |
XIE Xing-Long, MA Xue-Mei, LONG Hui, MING Yuan-Yuan, SUN Sheng. Curvelet transform-based denoising of resonance interference induced by electrical poles in seismic exploration[J]. Geophysical and Geochemical Exploration, 2022, 46(2): 474-481. |
| [2] |
ZHANG Yang, WANG Jun-Heng, CAO Lian-Peng, FENG Yu-Hua, ZHU Jiang-Huang, FU Qiang. A study of the application of Curvelet transform to potential field signal extraction[J]. Geophysical and Geochemical Exploration, 2021, 45(1): 84-94. |
|
|
|
|

