E-mail Alert Rss
 

物探与化探, 2025, 49(1): 148-157 doi: 10.11720/wtyht.2025.2548

方法研究信息处理仪器研制

基于聚类分析的ModEM三维反演复杂地形网格剖分

胡士晖,, 闵刚,, 孙浥钦, 陈春江, 李春婷, 张志豪

成都理工大学 地球物理学院,四川 成都 610059

Gridding of complex terrains based on cluster analysis for ModEM 3D inversion

HU Shi-Hui,, MIN Gang,, SUN Yi-Qin, CHEN Chun-Jiang, LI Chun-Ting, ZHANG Zhi-Hao

College of Geophysics, Chengdu University of Technology, Chengdu 610059, China

通讯作者: 闵刚(1983-),男,博士(后),副教授,主要从事地球探测与信息技术、构造地球物理等方面的教学与科研工作。Email:mg-s1983827@163.com

第一作者: 胡士晖(1999-),男,成都理工大学在读硕士研究生。Email:shihuihu_cdut@163.com

责任编辑: 王萌

收稿日期: 2023-12-19   修回日期: 2024-03-7  

基金资助: 深地国家科技重大专项“深部高温地热能探深评价及开发利用示范”(SQ2024AAA060115)
国家自然科学基金重点项目“基于深度学习的青藏高源深部电性结构模型及其动力学特征”(41930112)

Received: 2023-12-19   Revised: 2024-03-7  

摘要

地形因素对大地电磁三维反演结果有显著影响,虽然前人在压制地形影响上已经取得了丰富的研究成果,但在复杂地形(高程变化大)的网格剖分上还存在设计网格复杂与数据高程点校正困难的问题。本文针对主流大地电磁三维反演模块ModEM,提出了一种基于无监督学习的快速带地形网格自动设计剖分新方法,核心内容包括K-means++算法和聚类效果评价,与不考虑地形的均匀分层、等比分层方法相比具有以下优点:①基于聚类的分层方法生成的地形网格具有更高的地形近似度,将地形网格与实际地形之间的平均误差降低了25%;②一定程度上避免了数据高程地形改正的匹配计算;③不仅可用于快速的设计地形网格,其分层特点还可以被参考用于其他建模软件的网格剖分。利用该方法演示了某矿区复杂地形高程数据剖分的全部流程,生成了更能代表实际地形特征的电阻率结构模型,并基于该模型获得了更加精细的三维反演结果。理论和实际应用说明该方法极大地提高了网格剖分的地形适应性,对于压制大地电磁三维反演地形影响具有重要的意义。

关键词： 音频大地电磁法; ModEM; 地形网格剖分; K-means++

Abstract

The topographic factor significantly influences the 3D inversion results of magnetotelluric data. Despite extensive research results previously obtained in suppressing topographic effects, the gridding of complex terrains (with significant elevation changes) is still challenged by grid design complexity and difficulty in correcting data elevation points. Based on the mainstream 3D inversion module ModEM for magnetotelluric data, this study proposed a novel method for rapid automatic grid design and partitioning of terrains based on unsupervised learning, primarily involving the K-means++ algorithm and the assessment of clustering effects. Compared to the uniform and equal proportion-based hierarchical methods ignoring the topographic factor, the proposed method shows the following advantages: (1) The terrain grid generated by the clustering-based hierarchical method manifested higher terrain approximation, reducing the average error between the terrain grid and the actual terrain by 25%; (2) The matching calculation for terrain correction based on the digital elevation model was somewhat avoided; (3) The rapid design of terrain grids can be achieved, and the hierarchical characteristics can be referenced for gridding in other modeling software. The proposed method was employed to demonstrate the whole process of partitioning the elevation data of a complex terrain in a mining area, generating a resistivity structure model more representative of the actual terrain characteristics. Based on this model, finer-scale 3D inversion results were obtained. Theoretical and practical applications illustrate that the proposed method can significantly improve the topographic adaptability of gridding, holding critical significance for suppressing topographic effects on the 3D inversion of magnetotelluric data.

Keywords： audio-frequency magnetotellurics; ModEM; terrain gridding; K-means++

PDF (5917KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

胡士晖, 闵刚, 孙浥钦, 陈春江, 李春婷, 张志豪. 基于聚类分析的ModEM三维反演复杂地形网格剖分[J]. 物探与化探, 2025, 49(1): 148-157 doi:10.11720/wtyht.2025.2548

HU Shi-Hui, MIN Gang, SUN Yi-Qin, CHEN Chun-Jiang, LI Chun-Ting, ZHANG Zhi-Hao. Gridding of complex terrains based on cluster analysis for ModEM 3D inversion[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 148-157 doi:10.11720/wtyht.2025.2548

0 引言

大地电磁测深的反演问题一直是地球物理工作者研究的重点[1]。模块化反演系统ModEM[2-3](modular system for inversion of electromagnetic geophysical data)在大地电磁勘探中已得到广泛应用,其三维NLCG反演算法得到地球物理研究人员的普遍认可[4⇓-6]。NLCG法反演速度较快,但较依赖初始模型和经验参数输入,否则效果较差,具有一定的偶然性和盲目性[7]。重大工程建设与矿产资源勘查等方面的地球物理勘探应用场景,相对于壳幔深部结构研究,一般具有勘探深度浅、地形复杂等特点,且复杂地形对反演结果的影响不能被忽略[8⇓⇓-11],因此地形因素对大地电磁反演结果的影响受到越来越多的重视[12-13]。

但是,对地形复杂区域进行ModEM三维反演的网格剖分时,现有方法通常采用人工经验划分等距或等比层位,未能充分考虑地形自身特征,因此反演网格与实际地形往往存在较大差别,也会带来网格高程校正过程复杂的问题。为提高反演结果的准确性以及划分地形网格的效率,便捷设计更高的地形拟合度网格尤为必要。ModEM使用的是交错网格,通常认为网格单元大小影响地形近似程度。为了更加准确地表示地形,增加网格数量是一种有效提高地形近似度的方法,但随着网格数量的增加,收敛性变差[14],反演的速度迅速降低[15]。秦策等[13]通过ModEM反演不同网格大小的大地电磁模型,发现大网格出现虚假异常,而小网格结果对高阻体异常反映很弱,结果表明网格过于稀疏导致地形近似程度低,而网格过密可能导致更强的反演非唯一性。

生成ModEM地形网格数据,常用的有开源库MTpy[16-17]以及Arseny Shlykov开发的免费软件EMP[18],它们对于地形处理具有不同的解决方案。在MTpy中可以读取WS3INV3D等模型文件用于创建带地形三维反演文件,也可以读取地形文件或利用测点的高程数据插值计算每一个模型网格上的高程值创建曲面。EMP中可以通过导入点云数据进行插值或者导入特定形式的grd文件等曲面数据来创建曲面。MTpy与EMP都可以通过指定曲面上方或下方电阻率值填充模型对应区域单元,创建带地形三维反演文件。但仍然需要人为地预先划分层位,然后根据测点高程和曲面进行地形网格校正。

为了用更少的网格数量来达到更高的地形近似程度,同时简化网格设计步骤,本文提出一种设计地形网格层位的新方法,即采用无监督学习对复杂地形高程数据聚类[19]。该方法通过预先考虑地形本身特征来替代人为的层位划分,得到高拟合度的地形网格。同时将实际测点聚类到最近的地形层位,简化了数据高程地形改正的计算问题,显著地提升了网格设计效率。

1 K-means++原理与聚类评估技术

1.1 K-means++算法

K-means++聚类算法是K-means算法的改进[20-21]。K-means算法是一种基于距离划分的聚类算法[22],是最典型的聚类方法之一[23],它将n个观测值分配给由质心定义的k个簇之一[24⇓⇓-27]。其算法步骤如下:通过选择k个初始簇中心计算所有观测值与每个对应簇中心距离,常用的距离为欧式距离,如下式所示:

dis(Xi,Cj)=(Xi-Cj)2　

式中:Xi表示第i个观测值1≤i≤n;Cj表示第j个簇中心1≤j≤k。

依次比较并将每个观察值分配给离质心最近的簇。计算每个簇中观测值平均值,确定新的簇中心位置,如式(2)所示:

Cj=∑Xi∈SjXiSj

式中:Cj表示第j个簇中心1≤j≤k;Xi表示第i个观测值1≤i≤n;Sj代表第j个簇1≤j≤k;Sj代表第j个簇的观测值个数。重复2~4次迭代得到k个簇S1,S2,…,Sk。

K-means算法对初始簇中心过于敏感[28⇓-30],容易陷入局部最优,其改进算法K-means++能够初始化簇中心,并且能够使簇之间距离间隔尽可能的远,降低对于初始簇中心的敏感性。K-means++在计算簇内点到簇中心欧氏距离计算和时,能够比K-means更快收敛到更低的总和[31-32]。

1.2 聚类评估技术

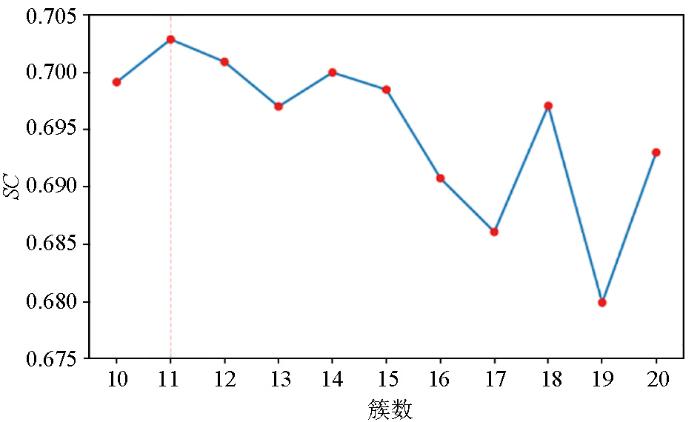
1.2.1 轮廓系数评估技术

轮廓系数[33](silhouette coefficient),即SC值。它是一种结合内聚度和分离度两种因素构建的一种聚类评估值,能够评价聚类算法在不同的运行方式中对聚类结果产生的影响。

SCx=bx-axmaxax,b(x)

式中:x为各个观测值,a(x)为内聚度值,表示x与所属簇的紧凑性,值越小,表示所聚类结果越紧凑;b(x)为分离度值,表示x与其他簇的分离程度,值越大,x与其他簇分离程度越高。轮廓系数可评价不同聚类参数设置下的算法效果,-1≤SC(x)≤1,当SC值接近1时,表明x所在簇是紧凑的,且远离其他簇[34]。

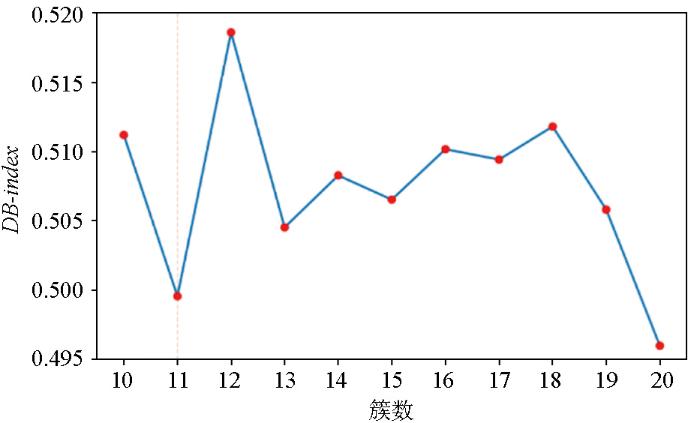
1.2.2 DB-index评估技术

DB-index(DBI)指数[35]是一种用于评估聚类结果质量的指标。它通过计算簇内与簇间距离的比率,来找出观测值集合中最佳聚类数或评估给定聚类的质量,DB-index值计算如下所示:

DB=1k∑j=1kmaxj≠i{Di,j}
Di,j=(di-+dj-)di,j

式中:di-表示第i个簇中每个点到第i个簇中心的平均距离;dj-表示第j个簇中每个点到第j个簇中心的平均距离;di,j代表第i个簇中心与第j个簇中心的欧式距离。DB-index评估技术通过整合簇内聚合度和簇间分离度能较全面地评价聚类的优劣。DB-index值越小表示聚类结果越好,它可以用于选择最佳的聚类数目。

1.2.3 间隙值统计评估技术

间隙值统计(gap statistic)[36]是一种对于肘部法则的改进。相比传统肘部法则,间隙值统计法为了避免受数据本身聚类结构的影响,使用蒙特卡洛模拟增加了随机参考数据集,使聚类簇数量k的选择更加稳健。通过定位将“肘”位置估计为最大间隙值的簇数量来形式化该方法,最优簇数量对应一定容差范围内局部或全局间隙值最大的解。

2 MODEM复杂地形网格剖分方法

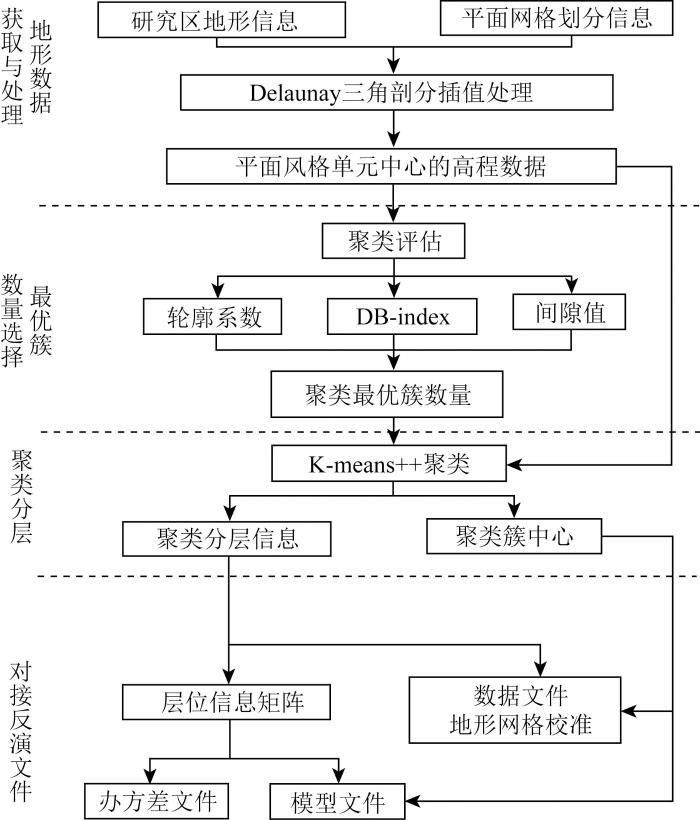
在实际设计MODEM反演网格中,深度上的网格划分需要花费很大的工作量,因为不仅需要考虑拟合地形,还需要考虑测点高程必须位于地形网格上。图1给出了复杂地形网格建立以及对接MODEM反演文件的流程示意,主要步骤有:地形数据获取与处理、最优簇数量的选择、聚类分层、对接反演文件。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   聚类建模对接MODEM流程

Fig.1   Flowchart of cluster modeling for MODEM


2.1 地形数据获取与处理

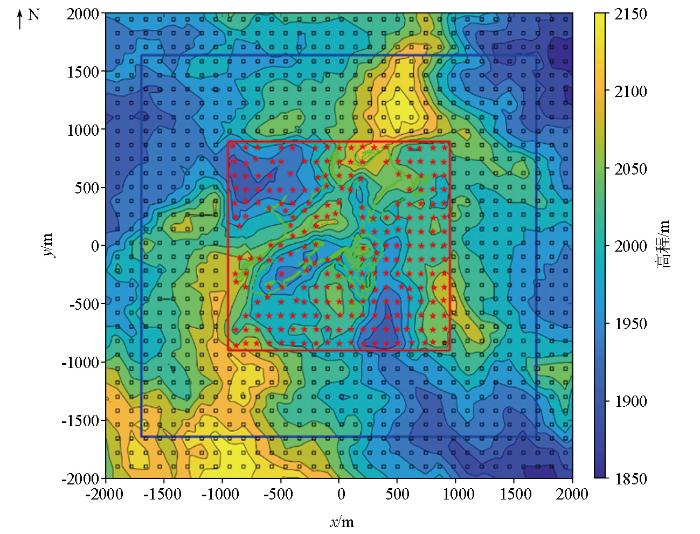
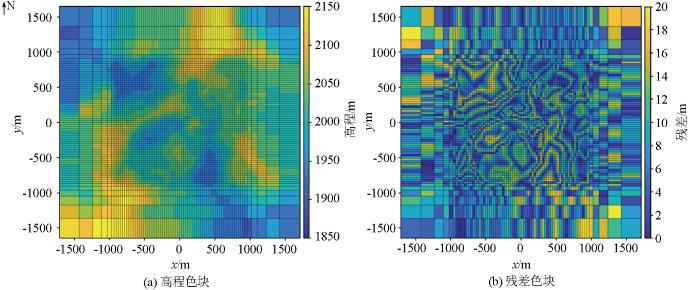
研究区域位于北方某矿区,工区南北1.6 km,东西1.8 km,地形高差约300 m。本文所使用的地形高程数据(图2)来源于实测采集和公共的数字高程模型(DEM)数据:

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   高程数据来源位置分布(红色星状点代表音频大地电磁GPS测点,绿色圆点代表路线上的GPS高程数据,黑色方形点代表ASTER GDEM V2的DEM数据,红色框代表研究区域,蓝色框代表扩展网格区域)

Fig.2   Location distribution map of elevation data (the red star points represent the GPS points of AMT stations, the green dots represent the GPS points along the route, the black square points represent the DEM data from the ASTER GDEM V2, the red rectangle represent research location area, the bule rectangle represent extended location area)


1)实测高程数据。在研究区域内共布设了242个音频大地电磁测点,频率范围为0.35~10 400 Hz,南北点距约120 m,东西点距约100 m。在每个电磁测点及附近道路上均采用GPS定位掌机接收差分信号记录定解高程(HRMS限制2.0,VRMS限制2.0)。

2)DEM数据。对研究区域外的部分使用ASTER GDEM V2的DEM数据(分辨率为1弧秒)。

在第一部分数据的处理中,把实测高程数据减去手持GPS高度的值作为研究区范围内实际高程数据。为了避免外插值产生不合理高程数据,引入第二部分DEM数据作为研究区外的高程。

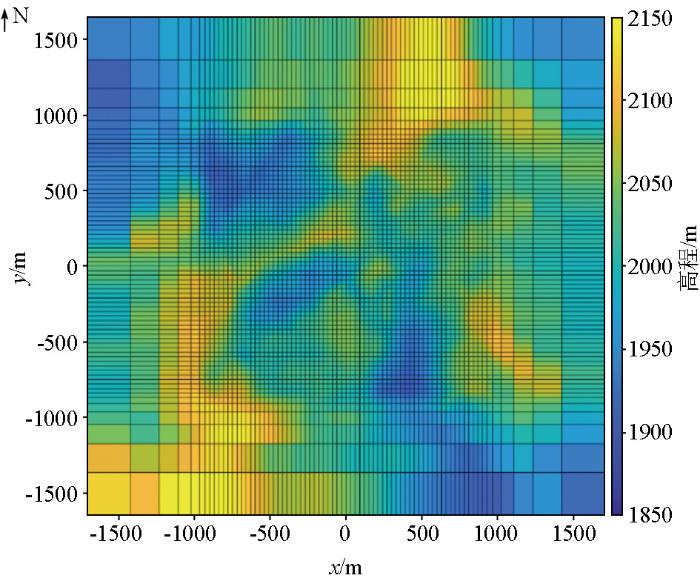
由于矿区位于北方,风化导致岩石有一定切割,高程变化多呈线性,所以根据区域特点来选择插值类型。最终选择合并数据并利用Delaunay三角剖分[37]进行线性内插值处理,获取所有网格单元中心位置的插值高程数据,如图3所示。从图中可以看出插值前后研究区内特征相似,研究区内北西和南东角地势低处的刻画良好,呈条带状特征的地势高点也能很好地对应。本文使用上述插值高程数据近似作为研究区域与扩展网格范围内的实际地形。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   实际地形网格高程色块

Fig.3   Actual terrain grid elevation color block map


2.2 最优簇数量选择

K-means++算法作为一个半监督学习算法,需要预先给出簇数量,对于簇数量的选择,可以通过合适的聚类评价指标参考。水平网格间距一般为测点点距的1/4~1/5,因此研究区域网格大小设置为30 m。过疏过密的网格都会对反演结果造成负面影响,采用0.5~1倍网格大小的层间距较为合适,研究区高差约300 m,因此确定簇数量的探测范围为10~20簇。然后对范围内簇数量分别采用间隙值、DB-index和轮廓系数进行评价聚类效果。由于过密网格会降低反演效率,因此以各指标的首个最优值作为最优簇数量参考(如图4~6中红色虚线)。

图4

新窗口打开| 下载原图ZIP| 生成PPT

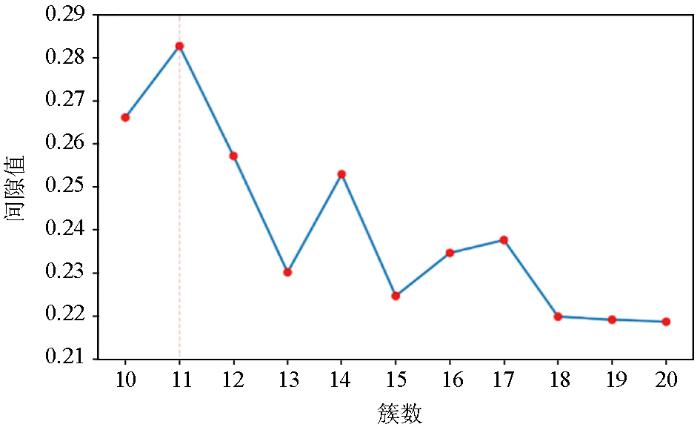
图4   间隙值评估优选簇数量

Fig.4   Gap statistic evaluates the number of preferred clusters chart


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   DB-index评估优选簇数量

Fig.5   DB-index evaluation of the number of preferred clusters chart


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   轮廓系数评估优选簇数量

Fig.6   SC evaluation of the number of preferred clusters chart


间隙值优选结果如图4,间隙值选择最优标准为一定容差范围内局部或全局间隙值最大的值,图中显示簇数量为11时为全局间隙值最大值。DB-index优选结果如图5,DB-index值越小表示簇间相似度越低,从而具有越好的聚类结果,图中显示簇数量为11时是首个最优簇数量值。轮廓系数优选结果如图6,当SC值接近1时,表明x所在簇是紧凑的,且远离其他簇,图中显示簇数量为11时最接近1。综合3种指标结果,选择11作为最终的最优聚类数。该数量能够综合考虑数据的簇内聚合度和簇间分离度,以11作为输入K-means++聚类划分的簇数量值可以获得最好的效果。

2.3 聚类效果分析

为了对比聚类的效果,本文建立了3种不同的地形划分模型:聚类网格模型、均匀网格模型和等比网格模型。聚类网格模型的高程通过簇为11的K-means++算法计算获取11个分层;均匀网格模型通过均匀划分获取11个分层;等比网格模型通过等比系数(q)为1.1向下递增的划分方式获取11个分层。这些模型的层中心划分结果见表1。然后通过最邻近原则将高程点划分到各层位。最后分别对这3种模型的分层结果与图3所示的网格化高程值进行误差分析。

表1   地形划分模型分层结果

Table 1  Topographic modeling stratification results

网格高程层号聚类方法
分层位置/m		均匀方法
分层位置/m		等比方法
分层位置/m
12137.52160.52164.9
22098.22135.32147.6
32073.42110.12128.6
42052.92084.92107.7
52036.12059.72084.7
62020.72034.42059.4
72005.52009.22031.5
81989.91984.02000.9
91970.41958.81967.2
101950.11933.61930.1
111927.71908.41889.4

新窗口打开| 下载CSV


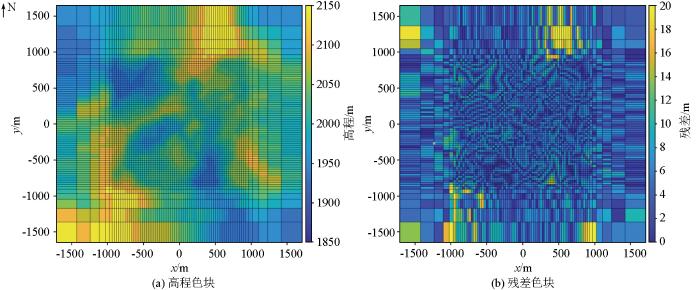
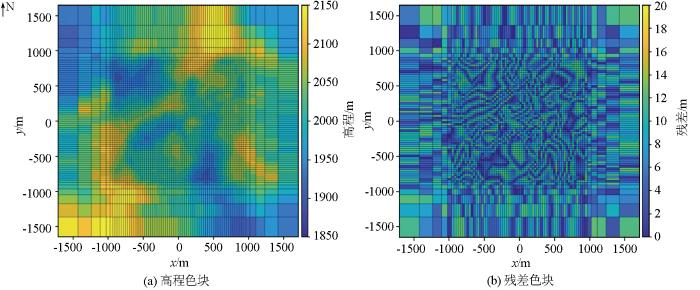
本文通过误差平均值、误差均方差进行误差分析,同时引入确定系数(R-square)来比较不同划分方法的拟合效果,确定系数可以用来表征一个拟合的好坏,确定系数越高,表明模型对数据的拟合越好。

通过对各模型分层效果(如图7~9)与图3网格化后的高程进行对比发现:聚类分层方法的地形网格各单元误差普遍较低,少部分区域具有较大的误差,主要集中在扩展网格高地势与低地势的区域;均匀划分高程网格得到的地形网格整体误差偏高,误差分布均匀;等比划分高程网格得到的地形网格整体误差较高,其中高地势区域误差较小,少部分区域具有较大误差,主要集中在低地势的区域。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   聚类网格高程色块

Fig.7   Clustered grid elevation color block map


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   均匀网格高程色块

Fig.8   Uniform grid elevation color block map


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   等比网格高程色块

Fig.9   Isometric grid elevation color block map


对以上不同网格划分方法的误差进行对比,结果见表2。可以看出基于聚类的分层方法生成的地形网格具有更高的地形近似度,与均匀划分方法相比,地形网格与实际地形之间的平均误差降低了25%。虽然聚类分层方法的地形网格部分区域具有较大误差,但是其均方差在所有划分方法中是最小的,这代表着K-means++聚类方法在降低误差的同时,可以较好地保持稳定性,即得到的离散值也是最小的。这可能是扩展网格相比研究区域稀疏,获取的高程值数量少,变相的降低了该区域聚类的权重,使其不能很好的拟合这些区域的离散值。

表2   网格高程误差分析

Table 2  Analysis of grid elevation error

网格高程
划分方法		误差平均值/m误差均方差/m确定系数
聚类划分4.77333.6720.984
均匀划分6.42454.2650.979
等比划分7.54777.7760.970

新窗口打开| 下载CSV


为了具体形象的表示地形近似度,我们对比了确定系数。通过对比可以看出K-means++聚类方法划分高程网格的确定系数最高,进而代表K-means++聚类方法划分层位在相同层位下具有更高的地形近似度。

2.4 对接反演文件

通过聚类可以获得分层信息的矩阵numsMatrix以及簇中心数组Layer,但应用于ModEM中还需要将其对接到指定的输入文件。以下4段Matlab代码的主要部分可以通过指定均匀空间电阻率值与空气电阻率值实现输出ModEM地形部分的模型文件。

第一段代码为脚本Outpuy_cov_ws_part.m,功能类似主函数,输入为聚类分层信息的矩阵numsMatrix和簇中心数组Layer;第二段代码为函数numsMatrix2cov.m,功能为输出协方差cov文件;第三段代码为函数numsMatrix2ws.m,功能为输出模型ws文件,其中res_object是均匀空间电阻率值,res_air是空气电阻率值;第四段代码为函数layer2dataele.m,功能为进行测点高程校正,输入的参数Data为测点的分层一维数组。

通过脚本代码Outpuy_cov_ws_part.m,可以获得ModEM三维反演所需要的模型ws文件,协方差cov文件,以及地形网格高程校正后的测点高程。

1)脚本代码:

  

Outpuy_cov_ws_part.m
numsMatrix2cov(numsMatrix, Layer);
numsMatrix2ws(numsMatrix, Layer, res_object, res_air);
Dataele = layer2dataele(Data, Layer);

新窗口打开| 下载CSV


2)numsMatrix2cov函数主要代码:

  

numsMatrix2cov.m
function numsMatrix2cov(Data,Layer)
elev_layer = Data;
Layer = sort(Layer); %正向排序簇中心数组
max_depest_layer = length(Layer);
for i = 1:max_depest_layer %循环获得该层协方差矩阵并输出
temp = elev_layer';
test_value = max_depest_layer - i +1;
temp(temp < test_value) = 0;
temp(temp >= test_value) = 1;
temp_space = [i,i];
writematrix(temp_space,'cov部分.xls','WriteMode','append');
writematrix(temp,'cov部分.xls','WriteMode','append');
end
fclose('all');
end

新窗口打开| 下载CSV


3)numsMatrix2ws函数主要代码:

  

numsMatrix2ws.m
function numsMatrix2ws(Data,Layer,res_object,res_air)
elev_layer = Data;
Layer = sort(Layer);
max_depest_layer = length(Layer);
% Z为间隔,用于输出z方向网格间距
Z = Layer(2:end) - Layer(1:end-1);
Z = Z(end:-1:1);
res_object = log(res_object);
res_air = log(res_air);
out_ws = fopen('ws部分.txt','w+');
fprintf(out_ws,"%.2f\t",Z);
fprintf(out_ws,"\n\n");
%循环获得该层模型电阻率数组并输出
for i = 1:max_depest_layer
temp = elev_layer;
test_value = max_depest_layer - i +1; %
标识层位的变量
temp(temp >= test_value) = res_object +

新窗口打开| 下载CSV


  

(max_depest_layer + 1); temp(temp < test_value) = res_air + (max_depest_layer + 1);
temp = temp - (max_depest_layer + 1);
for k = 1:size(temp,1)
for j = 1:size(temp,2)
fprintf(out_ws,"%.5E\t",temp(k,j));
end
fprintf(out_ws,"\n");
end
fprintf(out_ws,"\n");
end
fclose('all');
end

新窗口打开| 下载CSV


4) layer2dataele函数主要代码:

  

layer2dataele.m
function Dataele = layer2dataele(Data,Layer)
Layer = max(Layer) - Layer; %深度网格以地面为0深度向下增加
for i = 1:length(Layer)
Data(Data == i) = Layer(i) + max(Layer);
end
Dataele = Data - max(Layer);
end

新窗口打开| 下载CSV


3 聚类剖分反演实例

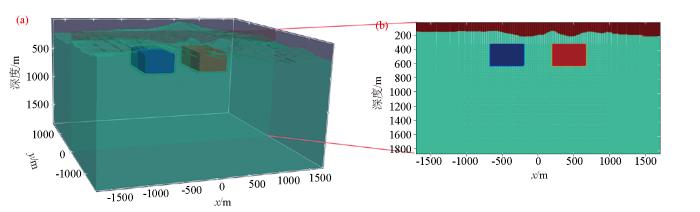
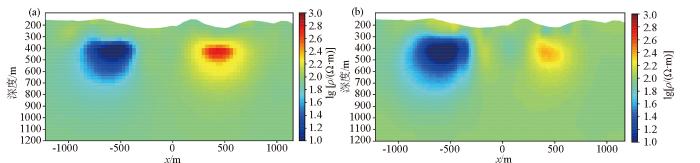
为了验证本文网格剖分方法的有效性,以层高5 m建立 60层地形部分模型,其误差平均值为1.255,误差均方差为2.112,确定系数为0.999。模型添加一个高阻异常体与一个低阻异常体(如图10a),高阻异常体以红色块表示,电阻率为1 000 Ω·m;低阻异常体以蓝色块表示,电阻率为10 Ω·m;均匀半空间电阻率为100 Ω·m。通过对该模型所得正演数据分别用聚类剖分网格和平均剖分网格进行反演,随后分别用基于聚类的层位划分方式与平均分层的划分方式进行反演,最终聚类剖分方式反演误差为2.05,平均剖分方式反演误差为2.14,反演结果见图11。通过对比相同界面上的正演模型(如图10b)可以发现平均分层的划分方式与聚类分层的划分方式反演结果均较好的体现了高低阻异常体。两种方式的反演结果均显示对高阻,低阻的体现具有差别,这是由于大地电磁法对于低阻体敏感。通过对比两种方式的反演结果不难发现,平均剖分网格方式的反演结果虽然能大致反映除异常体的埋深和轮廓,但是周围存在一些的虚假异常,对围岩电阻率的反映较差。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   正演模型

a—三维模型;b—模型切片(其中上方红色区域代表空气地形,蓝色块为低阻体,红色块为高阻体,图中点代表网格中心分布位置)

Fig.10   Forward Model

a—3D modeling figure;b—model slice figure(where the upper red area represents the air topography, the blue block is a low resistor, the red block is a high resistor, and the dots in the plot represent the locations of the grid center distributions)


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   反演结果

a—聚类剖分方式;b—平均剖分方式

Fig.11   Inversion results

a—clustering mode;b—average mode


4 结论及讨论

为了用更少的网格数量来达到更高的地形近似程度,同时简化网格设计步骤,本文提出一种设计地形网格层位的新方法,即采用无监督学习对复杂地形高程数据聚类。该方法通过预先考虑地形本身特征来替代人为的层位划分,得到高拟合度的地形网格。同时将实际测点聚类到最近的地形层位,简化了数据高程地形改正的计算问题,显著地提升了网格设计效率。

本文针对地形高程层位划分过密或过疏对反演结果造成的负面影响问题,提出一种基于聚类算法的新方法来优化地形层位划分。该方法利用聚类评估算法选择地形分层的最佳簇数,并使用K-means++算法进行聚类分层。

1)与均匀划分和等比划分方法相比,聚类分层方法划分的地形网格能够在垂直网格划分上获得更高的地形近似度,从而减少加密网格的需求,降低过密网格对反演的负面影响。

2)该方法简化了地形网格校正过程,提高了地形网格划分的效率。

实际上,为了更合理地划分地形层位,需要考虑电磁场的传播特点以及采集数据的频率信息等因素。然而,本文考虑的因素较少,仅利用了高程本身数据和平面网格大小进行地形网格划分。应考虑更多的反演影响因素,用更高的聚类维度进行层位划分,我们相信这种方法能够更准确、更高效地应用于ModEM三维反演中。

参考文献

李思平, 刘彩云, 熊杰, 等.

基于改进残差网络的大地电磁反演研究

[J]. 物探与化探, 2023, 47(6):1508-1518.

[本文引用: 1]

Li S P, Liu C Y, Xiong J, et al.

Magnetotelluric inversion based on an improved residual network

[J]. Geophysical and Geochemical Exploration, 2023, 47(6):1508-1518.

[本文引用: 1]

Egbert G D, Kelbert A.

Computational recipes for electromagnetic inverse problems

[J]. Geophysical Journal International, 2012, 189(1):251-267.

[本文引用: 1]

Kelbert A, Meqbel N, Egbert G D, et al.

ModEM:A modular system for inversion of electromagnetic geophysical data

[J]. Computers & Geosciences, 2014,66:40-53.

[本文引用: 1]

Yang B, Zhang A Q, Zhang S, et al.

Three-dimensional audio-frequency magnetotelluric imaging of Akebasitao granitic intrusions in Western Junggar,NW China

[J]. Journal of Applied Geophysics, 2016,135:288-296.

[本文引用: 1]

Min G, Yuan H L, Wang X B, et al.

Crustal and upper mantle electrical structure and uplift mechanism of the Liupanshan orogenic belt in the NE Tibetan Plateau

[J]. Tectonophysics, 2023,853:229799.

[本文引用: 1]

顾观文, 吴文鹂, 梁萌.

大地电磁三维正、反演多核并行计算的设计与实现

[J]. 物探与化探, 2014, 38(3):601-606.

[本文引用: 1]

Gu G W, Wu W L, Liang M.

The multi-core paralleled strategies and efficiency analysis of 3D magnetotelluric forward modeling and inversion

[J]. Geophysical and Geochemical Exploration, 2014, 38(3):601-606.

[本文引用: 1]

许第桥, 李茂.

二连盆地宽频大地电磁法数据精细反演处理研究——以满都拉图地区的数据为例

[J]. 物探与化探, 2023, 47(4):994-1001.

[本文引用: 1]

Xu D Q, Li M.

Fine inversion of the broadband magnetotelluric data of the Erlian Basin:A case study of the Mandulatu area

[J]. Geophysical and Geochemical Exploration, 2023, 47(4):994-1001.

[本文引用: 1]

顾观文, 李桐林.

基于矢量有限元的带地形大地电磁三维反演研究

[J]. 地球物理学报, 2020, 63(6):2449-2465.

DOI:10.6038/cjg2020N0321      [本文引用: 1]

研究了基于矢量有限元方法的大地电磁带地形三维反演算法并开发了三维反演计算程序代码.在大地电磁场正演数值模拟方面，采用并行直接稀疏求解器PARDISO且无需进行散度校正的快速正演方案，对典型地形模型，在中等规模计算条件下，与双共轭梯度法（BICG）计算结果比较，发现PARDISO比BICG快10倍以上；通过理论模型试算，并与前人的有限元法计算结果对比，验证了带地形三维正演计算程序的正确性.在反演方面，本研究基于共轭梯度方法编写了大地电磁带地形三维反演代码，为了避免直接求取雅可比矩阵，将反演中的雅可比矩阵计算问题转为求解两次"拟正演"问题，进而将PARDISO的快速正演方案应用于"拟正演"问题的求解，以提高反演计算效率.利用开发的反演算法对多个带地形地电模型的合成数据进行了三维反演，反演结果能很好地重现理论模型的电性结构，验证了本文开发的三维反演算法的正确性和可靠性.最后，利用该算法反演了某矿区大地电磁实测数据，反演得到的三维电性结构清晰地反映了研究区的地电特征，将反演结果与该区已有地质资料结合进行解释，应用效果明显，进一步验证了本文算法的有效性.

Gu G W, Li T L.

Three-dimensional magnetotelluric inversion with surface topography based on the vector finite element method

[J]. Chinese Journal of Geophysics, 2020, 63(6):2449-2465.

[本文引用: 1]

Xiong B, Luo T Y, Chen L W, et al.

Influence of complex topography on magnetotelluric-observed data using three-dimensional numerical simulation:A case from Guangxi area,China

[J]. Applied Geophysics, 2020, 17(4):601-615.

[本文引用: 1]

何帅, 杨炳南, 阮帅, 等.

三维AMT正反演技术对贵州马坪含金刚石岩体探测的精细解释

[J]. 物探与化探, 2022, 46(3):618-627.

[本文引用: 1]

He S, Yang B N, Ruan S, et al.

Fine Interpretation of the exploration results of diamond-bearing rock masses in Maping area,Guizhou using the 3D AMT forward modeling and inversion technologies

[J]. Geophysical and Geochemical Exploration, 2022, 46(3):618-627.

[本文引用: 1]

程正璞, 郭淑君, 魏强, 等.

AMT地形影响与带地形反演研究

[J]. 物探与化探, 2023, 47(1):146-155.

[本文引用: 1]

Cheng Z P, Guo S J, Wei Q, et al.

Audiomagnetotelluric data:Influence of terrain and the inversion considering terrain

[J]. Geophysical and Geochemical Exploration, 2023, 47(1):146-155.

[本文引用: 1]

秦策, 刘幸飞, 王绪本, 等.

基于自适应有限元正演的大地电磁法三维反演算法研究

[J]. 地球物理学报, 2022, 65(6):2311-2325.

[本文引用: 2]

Qin C, Liu X F, Wang X B, et al.

Three-dimensional inversion of magnetotelluric based on adaptive finite element method

[J]. Chinese Journal of Geophysics, 2022, 65(6):2311-2325.

[本文引用: 2]

Koldan J, Puzyrev V, de la Puente J, et al.

Algebraic multigrid preconditioning within parallel finite-element solvers for 3D electromagnetic modelling problems in geophysics

[J]. Geophysical Journal International, 2014, 197(3):1442-1458.

[本文引用: 1]

Zhdanov M S, Smith R B, Gribenko A, et al.

Three-dimensional inversion of large-scale EarthScope magnetotelluric data based on the integral equation method:Geoelectrical imaging of the Yellowstone conductive mantle plume

[J]. Geophysical Research Letters, 2011, 38(8):L08037.

[本文引用: 1]

Krieger L, Peacock J R.

MTpy:A Python toolbox for magnetotellurics

[J]. Computers & Geosciences, 2014,72:167-175.

[本文引用: 1]

Kirkby A, Zhang F, Peacock J, et al.

The MTPy software package for magnetotelluric data analysis and visualisation

[J]. Journal of Open Source Software, 2019, 4(37):1358.

[本文引用: 1]

Shlykov A.

Electromagnetic processor 1.4 user manual

[R]. Saint Petersburg State University St.Peterburg Russia, 2022.

[本文引用: 1]

陈军林, 彭润民, 李帅值, 等.

利用自组织特征映射神经网络和K-means聚类算法挖掘区域化探数据中的地质信息

[J]. 物探与化探, 2017, 41(5):919-927.

[本文引用: 1]

Chen J L, Peng R M, Li S Z, et al.

Self-organizing feature map neural network and K-means algorithm as a data excavation tool for obtaining geological information from regional geochemical exploration data

[J]. Geophysical and Geochemical Exploration, 2017, 41(5):919-927.

[本文引用: 1]

Beretta L, Cohen-Addad V, Lattanzi S, et al.

Multi-swap k-Means++

[J]. Eprint Arxiv, 2024.

[本文引用: 1]

Choo D, Grunau C, Portmann J, et al.

International Conference on K-means++:Few more steps yield constant approximation

[C]// 37th et al.International Conference on Machine Learning, 2020.

[本文引用: 1]

喻思羽, 李少华, 段太忠, 等.

基于局部各向异性的非平稳多点地质统计学算法

[J]. 物探与化探, 2017, 41(2):262-269.

[本文引用: 1]

Yu S Y, Li S H, Duan T Z, et al.

Non-stationary multiple-point geostatistics algorithm base on local anisotropy

[J]. Geophysical and Geochemical Exploration, 2017, 41(2):262-269.

[本文引用: 1]

刘凯, 戴慧敏, 刘国栋, 等.

基于主成分聚类法的典型黑土区土壤地球化学分类

[J]. 物探与化探, 2022, 46(5):1132-1140.

[本文引用: 1]

Liu K, Dai H M, Liu G D, et al.

Geochemical classification of the soil in a typical black soil area using the principal component analysis combined with K-means clustering algorithm

[J]. Geophysical and Geochemical Exploration, 2022, 46(5):1132-1140.

[本文引用: 1]

Lloyd S.

Least squares quantization in PCM

[J]. IEEE Transactions on Information Theory, 1982, 28(2):129-137.

[本文引用: 1]

杨俊闯, 赵超.

K-Means聚类算法研究综述

[J]. 计算机工程与应用, 2019, 55(23):7-14,63.

DOI:10.3778/j.issn.1002-8331.1908-0347      [本文引用: 1]

K-均值（K-Means）算法是聚类分析中一种基于划分的算法，同时也是无监督学习算法。其具有思想简单、效果好和容易实现的优点，广泛应用于机器学习等领域。但是K-Means算法也有一定的局限性，比如：算法中聚类数目K值难以确定，初始聚类中心如何选取，离群点的检测与去除，距离和相似性度量等。从多个方面对K-Means算法的改进措施进行概括，并和传统K-Means算法进行比较，分析了改进算法的优缺点，指出了其中存在的问题。对K-Means算法的发展方向和趋势进行了展望。

Yang J C, Zhao C.

Survey on K-means clustering algorithm

[J]. Computer Engineering and Applications, 2019, 55(23):7-14,63.

DOI:10.3778/j.issn.1002-8331.1908-0347      [本文引用: 1]

The K-Means algorithm is a partition-based algorithm in cluster analysis. With an unsupervised learning algorithm, its advantages of simple thinking, good effect and easy implementation are widely used in fields such as machine learning. But the K-Means algorithm also has certain limitations. For example, the K number of clusters in the algorithm is difficult to determine how to choose the initial cluster center, how to detect and remove outliers and the distance and similarity measure. This paper summarizes the improvement of K-Means algorithm from several aspects, and compares it with the classical K-Means algorithm. In addition, it analyzes the advantages and disadvantages of the improved algorithm, and points out the problems. Finally, the development direction and trend of K-Means algorithm are prospected.

周爱武, 于亚飞.

K-Means聚类算法的研究

[J]. 计算机技术与发展, 2011, 21(2):62-65.

[本文引用: 1]

Zhou A W, Yu Y F.

The research about clustering algorithm of K-means

[J]. Computer Technology and Development, 2011, 21(2):62-65.

[本文引用: 1]

Sinaga K P, Yang M S.

Unsupervised K-means clustering algorithm

[J]. IEEE Access, 2020,8:80716-80727.

[本文引用: 1]

Bury M, Schwiegelshohn C.

Random projections for k-means:Maintaining coresets beyond merge & reduce

[J]. Eprint Arxiv, 2015.

[本文引用: 1]

Cohen M B, Elder S, Musco C, et al.

Dimensionality reduction for k-means clustering and low rank approximation

[C]// Proceeding of the Forty-Serenth Annual, 2002.

[本文引用: 1]

Grunau C, Rozhoň V.

Adapting k-means algorithms for outliers

[C]// International Conference on Machine Learning,ACM Symposium on Theory of Computing(STOC’15),2015.

[本文引用: 1]

Arthur D, Vassilvitskii S.

K-means++ the advantages of careful seeding

[C]// Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. 2007.

[本文引用: 1]

Yoder J Priebe C E.

Semi-supervised K-means++

[J]. Journal of Statistical Computation and Simulation, 2017, 87(13):2597-608.

[本文引用: 1]

Rousseeuw P J.

Silhouettes:A graphical aid to the interpretation and validation of cluster analysis

[J]. Journal of Computational and Applied Mathematics, 1987,20:53-65.

[本文引用: 1]

Han J, Pei J, Tong H. Data mining:concepts and techniques[M]. San Francision: Morgan Kaufmann, 2022.

[本文引用: 1]

Davies D L, Bouldin D W.

A cluster separation measure

[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2):224-7.

PMID:21868852      [本文引用: 1]

A measure is presented which indicates the similarity of clusters which are assumed to have a data density which is a decreasing function of distance from a vector characteristic of the cluster. The measure can be used to infer the appropriateness of data partitions and can therefore be used to compare relative appropriateness of various divisions of the data. The measure does not depend on either the number of clusters analyzed nor the method of partitioning of the data and can be used to guide a cluster seeking algorithm.

Tibshirani R, Walther G, Hastie T.

Estimating the number of clusters in a data set via the gap statistic

[J]. Journal of the Royal Statistical Society Series B:Statistical Methodology, 2001, 63(2):411-423.

[本文引用: 1]

Amidror I.

Scattered data interpolation methods for electronic imaging systems:A survey

[J]. Journal of Electronic Imaging, 2002,11:157-176.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com