CSRMT正交水平发射源电磁场分布规律研究

doi:10.11720/wtyht.2024.1395

CSRMT正交水平发射源电磁场分布规律研究

陈兴朋^,¹, 王亮^,¹, 龙霞¹, 席振铢², 亓庆新¹, 薛军平¹, 戴云峰³, 胡子君⁴

1.湖南五维地质科技有限公司,湖南长沙 410205

2.中南大学地球科学与信息物理学院,湖南长沙 410083

3.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏南京 210029

4.湖南女子学院信息科学与工程学院,湖南长沙 410004

Distribution patterns of the electromagnetic fields of orthogonal horizontal magnetic dipoles as sources in CSRMT

CHEN Xing-Peng^,¹, WANG Liang^,¹, LONG Xia¹, XI Zhen-Zhu², QI Qing-Xin¹, XUE Jun-Ping¹, DAI Yun-Feng³, HU Zi-Jun⁴

1. Hunan 5D Geosciences Co. Ltd., Changsha 410205, China

2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China

3. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China

4. School of Information Science and Engineering, Hunan Women's University, Changsha 410004, China

通讯作者: 王亮(1989-),男,2013年硕士毕业于中南大学,从事电磁法勘探正反演算法与可视化软件的研究与应用。Email:leftwillow@163.com

第一作者: 陈兴朋(1986-),男,2012年硕士毕业于中南大学,从事电磁法仪器的开发与应用研究。Email:bantianfeng@foxmail.com

责任编辑: 朱晓颖

收稿日期: 2023-09-15 修回日期: 2023-12-29

基金资助:

国家重点研发计划课题(2022YFC2903404)
国家重点研发计划课题(2022YFC2900002)

Received: 2023-09-15 Revised: 2023-12-29

摘要

可控源射频大地电磁法(controlled source radio-magnetotellurics,CSRMT)测量通常使用发送频率1~1 000 kHz的人工场源,正交水平电偶源和正交水平磁偶源是人工源电磁法众多发射源中实现张量电阻率测量的优质场源。为此,本文基于水平电偶极子源和水平磁偶极子源电磁场解析公式,计算了均匀半空间模型正交水平电偶极子源和正交水平磁偶极子源的电磁场。结果表明,发射频率大于100 kHz时,应考虑位移电流;而张量视电阻率和阻抗相位在远区可以忽略位移电流的影响;固定模型电阻率、改变收发距时,模型计算表明高频电磁场远区测量范围更大;固定收发距、改变模型电阻率时,模型计算表明电磁场远区范围受电阻率影响较大,高阻模型需要更高的频率才会出现远区观测条件。磁偶源相较于电偶源,在张量视电阻率和相位上与实际值的偏差更小,更适于地质分析。

关键词： 可控源射频大地电磁法; 正交水平电偶源; 正交水平磁偶源; 位移电流; 阻抗

Abstract

Controlled source radio-magnetotellurics (CSRMT) measurements typically use artificial field sources transmitting at frequencies ranging from 1 to 1 000 kHz. Among the many transmitting sources of the artificial source electromagnetic method, the orthogonal horizontal electric dipole source and the orthogonal horizontal magnetic dipole source are preferred field sources for tensor resistivity measurements. Hence, using the analytical formulas for electromagnetic fields based on the horizontal electric dipole source and the horizontal magnetic dipole source, this study calculated the electromagnetic fields based on the orthogonal horizontal electric dipole source and the orthogonal horizontal magnetic dipole source in the homogeneous half-space model. The results show that: (1) The displacement current needs to be considered at transmitting frequencies above 100 kHz; (2) The effects of displacement current on the tensor apparent resistivity and the impedance phase can be ignored in the far zone; (3) With a constant model resistivity and varying distances between transmitter and receiver, model calculations indicate a larger measurement range in the far zone of the high-frequency electromagnetic field; (4) With a constant distance between transmitter and receiver and varying model resistivities, model calculations suggest that the far-zone range of the electromagnetic field is significantly influenced by resistivity, and that the high-resistivity model requires higher frequencies for achieving far-zone observation conditions.Compared with the electric dipole source, the magnetic dipole source exhibits smaller deviations on the tensor apparent resistivity and impedance phase with the actual value, which is more suitable for geological analysis.

Keywords： controlled source radio-magnetotellurics (CSRMT); orthogonal horizontal electric dipole source; orthogonal horizontal magnetic dipole source; displacement current; impedance

PDF (7800KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈兴朋, 王亮, 龙霞, 席振铢, 亓庆新, 薛军平, 戴云峰, 胡子君. CSRMT正交水平发射源电磁场分布规律研究[J]. 物探与化探, 2024, 48(3): 721-735 doi:10.11720/wtyht.2024.1395

CHEN Xing-Peng, WANG Liang, LONG Xia, XI Zhen-Zhu, QI Qing-Xin, XUE Jun-Ping, DAI Yun-Feng, HU Zi-Jun. Distribution patterns of the electromagnetic fields of orthogonal horizontal magnetic dipoles as sources in CSRMT[J]. Geophysical and Geochemical Exploration, 2024, 48(3): 721-735 doi:10.11720/wtyht.2024.1395

0 引言

可控射频大地电磁法(controlled source radio-magnetotelluric method,CSRMT)是一种新型的频率域近地表电磁测深方法^[1]。它以传统的大地电磁法(magnetotelluric,MT)为基础,通过建立可移动的人工发射源,并在远区观测各电磁场的分量来推演地下结构,其观测频率为1~1 000 kHz,远高于传统大地电磁类方法,探测深度为数米至百米^{[2⇓⇓⇓-6]}。正交水平电偶源和磁偶源是CSRMT法中常用的人工发射源,相较于单一偶极发射源,它们采用两个相互垂直的偶极发射源,因此能够实现张量CSRMT测量^[7-8]。这种测量方式的独特之处在于,它不仅能够获取任意测量方向的视电阻率,还能够提供一系列评判地下构造复杂性的参数,如倾子、二维判别椭圆等^[9-10],通过对这些参数的深入分析,能够更为详细地认识地下的地质结构。正交水平发射源的运用,使得CSRMT法在应对地质结构复杂的地区时展现出较好的适应性和应用价值^[2,11]。目前,CSRMT法在矿产资源、工程地质、水文地质和环境地质勘查等^{[12⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-25]}方面得到了广泛的应用,已经成为一种重要的近地表电磁测深方法。

近年来,随着不少浅层地球物理勘查中开始应用CSRMT方法^[4,11,26-27],CSRMT场源的分布规律和场源的选择亟需研究。席振铢等^[28-29]计算了忽略位移电流时准静态条件下,水平电偶源、水平磁偶源、正交水平电偶源以及正交水平磁偶源的电磁场的分布情况。Shlykov and Saraev^[30]研究了波动效应在水平电偶源中的影响,但没有给出其电磁场的分布规律和计算过程。CSRMT发送频率较高,可达1 000 kHz,对于一般的大地介质,在发送频率小于100 kHz时,传导电流远大于位移电流,可以忽略位移电流对电磁场分布的影响;当频率大于100 kHz时,位移电流的作用对场的影响随频率增大而不断增强,此时不能再忽略位移电流;对于有耗介质,当频率远大于1 000 kHz时,位移电流远大于传导电流,探地雷达的发送频率就处于该段频率范围内。CSRMT在频率范围100~1 000 kHz时,不再适用于忽略位移电流的准静态条件,因此对考虑位移电流的电磁场的分布规律研究势在必行^[31]。

本文基于横向电磁波传播原理^[32-33],推导了包含位移电流的水平电偶源和水平磁偶源电磁场公式,分别计算了正交水平电偶源和正交水平磁偶源的电磁场分布规律;在均匀半空间,考虑位移电流情形下讨论CSRMT的张量阻抗分布特征,忽略位移电流时的张量阻抗进行对比,计算两者的张量电阻率和阻抗相位的误差;在CSRMT频率范围内(1~1 000 kHz),分析了正交水平电偶源和正交水平磁偶源收发距和电阻率变化对张量电阻率和阻抗相位的影响,为野外施工在源的选择上,提供一定的理论支撑。

1 基本理论

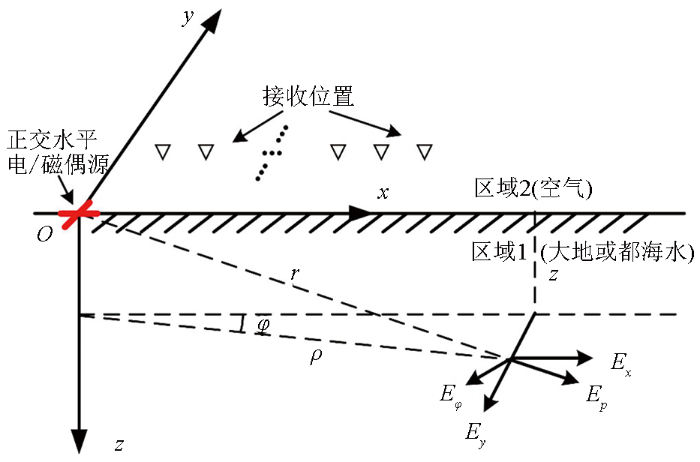
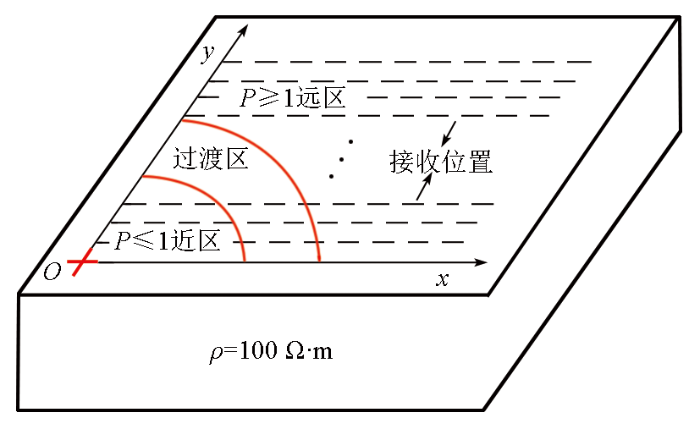
CSRMT使用的正交电偶源和正交磁偶源产生的电磁场影响范围小于200 km属于近距离传播的电磁场^[34],可以忽略电离层和地球曲率的影响。建立如图1所示的坐标系,取z轴垂直向下为正,区域1为地下,区域2为空气。设水平电偶/磁偶极子位于(0,0,0)点,偶极子方向y方向。图1中给出柱坐标系(ρ,φ,z)和笛卡尔坐标下(x,y,z)电场分布的示意图^[33]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 正交水平电/磁偶源在区域1产生电磁场示意图

Fig.1 The diagram of orthogonal horizontal electric or magnetic dipoles source generating electromagnetic field in region 1

推导了y方向水平磁偶极子产生的电磁场完整表达式为

(1)

\begin{array}{l} E_{1 ρ} = \frac{M}{2 π} s i n φ \int_{0}^{\infty} [k_{1}^{2} \frac{λ γ_{2}}{N} J_{0} (λ ρ) - \\ \frac{1}{ρ} \frac{λ^{2} (γ_{2} - γ_{1})}{N} J_{1} (λ ρ)] e^{- j γ_{2} z} d λ \end{array}

(2)

\begin{array}{l} E_{1 φ} = \frac{M}{2 π} c o s φ \int_{0}^{\infty} [\frac{λ γ_{1} (γ_{2} γ_{1} + λ^{2})}{N} J_{0} (λ ρ) + \\ \frac{1}{ρ} \frac{λ^{2} (γ_{2} - γ_{1})}{N} J_{1} (λ ρ)] e^{- j γ_{2} z} d λ \end{array}

(3)

\begin{array}{l} H_{1 ρ} = - \frac{M}{2 π ω μ_{0}} c o s φ \int_{0}^{\infty} [\frac{λ γ_{1} γ_{2} (γ_{1} γ_{2} + λ^{2})}{N} J_{0} (λ ρ) + \\ \frac{1}{ρ} \frac{λ^{2} (k_{1}^{2} + γ_{2}^{2} - γ_{1} γ_{2})}{N} J_{1} (λ ρ)] e^{- j γ_{2} z} d λ \end{array}

(4)

\begin{array}{l} H_{1 φ} = \frac{M}{2 π ω μ_{0}} s i n φ \int_{0}^{\infty} [k_{2}^{2} k_{1}^{2} \frac{λ}{N} J_{0} (λ ρ) \\ \frac{λ^{2} (k_{1}^{2} + γ_{2}^{2} - γ_{1} γ_{2})}{N ρ} J_{1} (λ ρ)] e^{- j γ_{2} z} d λ \end{array}

推导了y方向水平电偶极子产生的电磁场完整表达式为(推导过程见附录)

(5)

\begin{array}{l} E_{1 ρ} = - \frac{ω μ_{0} I d l}{2 π} c o s φ \int_{0}^{\infty} [\frac{γ_{1} γ_{2}}{N} J_{0} (λ ρ) + \\ \frac{λ}{ρ N} J_{1} (λ ρ)] λ e^{- j γ_{2} z} d λ \end{array}

(6)

\begin{array}{l} E_{1 φ} = \frac{ω μ_{0} I d l}{2 π} s i n φ \int_{0}^{\infty} [\frac{1}{M_{0}} J_{0} (λ ρ) - \\ \frac{λ}{ρ N} J_{1} (λ ρ)] λ e^{- j γ_{2} z} d λ \end{array}

(7)

\begin{array}{l} H_{1 ρ} = - \frac{I d l}{2 π} s i n φ \int_{0}^{\infty} [\frac{γ_{2}}{M_{0}} J_{0} (λ ρ) - \\ \frac{λ^{2} (γ_{2} - γ_{1})}{N} \frac{1}{λ ρ} J_{1} (λ ρ)] e^{- j γ_{2} z} λ d λ \end{array}

(8)

\begin{array}{l} H_{1 φ} = - \frac{I d l}{2 π} c o s φ \int_{0}^{\infty} [\frac{k_{2}^{2} γ_{1}}{N} J_{0} (λ ρ) + \\ \frac{λ^{2} (γ_{2} - γ_{1})}{N} \frac{1}{λ ρ} J_{1} (λ ρ)] λ e^{- j γ_{2} z} d λ \end{array}

其中,

(9)

\begin{array}{l} M_{0} = γ_{2} + γ_{1} & , & N = k_{2}^{2} γ_{1} + k_{1}^{2} γ_{2} \\ γ_{1} = \sqrt[]{k_{1}^{2} - λ^{2}} & , & γ_{2} = \sqrt[]{k_{2}^{2} - λ^{2}} \\ k_{1} = ω \sqrt[]{μ_{0} ε + i σ / ω} & , & k_{2} = ω \sqrt[]{μ_{0} ε_{0}} \end{array}

式中: $M$ 为发射磁矩; $γ_{1}$ 和 $γ_{2}$ 为反射系数; $ω$ 为角频率; $μ_{0}$ 为真空中磁导率; $ε_{0}$ 为真空中介电常数; $ε$ 为介质的介电常数; $σ$ 为介质的电导率; $k_{1}$ 和 $k_{2}$ 为波数;λ为波长; $J_{0}$ 和 $J_{1}$ 为计算汉克尔积分的滤波系数。

在准静态条件下忽略位移电流时,取 $k_{1} = ω \sqrt[]{i σ / ω}$ 。其中,1)均匀半空间水平电偶源产生的电磁场为^[30]

(10)

E_{ρ} = \frac{I d l}{2 π σ r^{3}} c o s φ [1 + e^{j k r} (1 - j k r)]

(11)

E_{φ} = \frac{I d l}{2 π σ r^{3}} s i n φ [2 - e^{j k r} (1 - j k r)]

(12)

\begin{array}{l} H_{ρ} = - \frac{3 I d l}{2 π r^{2}} s i n φ \{I_{1} (\frac{j k r}{2}) \cdot K_{1} (\frac{j k r}{2}) + \\ \frac{j k r}{6} [I_{1} (\frac{j k r}{2}) \cdot K_{0} (\frac{j k r}{2}) - I_{0} (\frac{j k r}{2}) \cdot K_{1} (\frac{j k r}{2})]\} \end{array}

(13)

H_{φ} = - \frac{I d l}{2 π r^{2}} c o s φ [I_{1} (\frac{j k r}{2}) \cdot K_{1} (\frac{j k r}{2})]

2)均匀半空间水平磁偶源产生的电磁场为^[30]

(14)$E_{x}=-\frac{j \mu \omega I \mathrm{~d} l}{2 \pi r^{2}} \sin \varphi \cos \varphi \{ -4 I_{1}\left(\frac{j k r}{2}\right) \cdot K_{1}\left(\frac{j k r}{2}\right)+$
$\frac{j k r}{2}\left[I_{0}\left(\frac{j k r}{2}\right) \cdot K_{1}\left(\frac{j k r}{2}\right)-I_{1}\left(\frac{j k r}{2}\right) \cdot K_{0}\left(\frac{j k r}{2}\right)\right]\},$

(15)$E_{y}=-\frac{j \mu \omega I \mathrm{~d} l}{2 \pi r^{2}} \sin \varphi \cos \varphi \{\left(1-4 \cos \varphi^{2}\right) I_{1}\left(\frac{j k r}{2}\right) \cdot K_{1}\left(\frac{j k r}{2}\right)+$
$\frac{j k r}{2}\left[I_{0}\left(\frac{j k r}{2}\right) \cdot K_{1}\left(\frac{j k r}{2}\right)-I_{1}\left(\frac{j k r}{2}\right) \cdot K_{0}\left(\frac{j k r}{2}\right)\right] \cos \varphi^{2} \},$

(16)

\begin{array}{l} H_{x} = - \frac{I d l}{2 π r^{5} k^{2}} \{3 + k^{2} r^{2} - (3 + 3 j k r - k^{2} r^{2}) e^{- j k r} + \\ c o s φ^{2} [- 15 - 3 k^{2} r^{2} + (- j k^{3} r^{3} - 6 k^{2} r^{2} + 15 j k r + 15) e^{- j k r}]\}, \end{array}

(17)

\begin{matrix} H_{y} = \frac{I d l}{2 π r^{5} k^{2}} [15 + 3 k^{2} r^{2} - (- j k^{3} r^{3} - 6 k^{2} r^{2} + 15 j k r + 15) e^{- j k r}] \end{matrix}

式中: $I_{1} (\frac{j k r}{2})$ 、 $K_{1} (\frac{j k r}{2})$ 和 $I_{0} (\frac{j k r}{2})$ 、 $K_{0} (\frac{j k r}{2})$ 分别为以 $\frac{j k r}{2}$ 为宗量的第一类和第二类虚宗量贝塞尔函数,下标表示贝塞尔函数的阶数。

2 电磁场的分布规律

2.1 考虑位移电流的正交水平电偶源和正交水平磁偶源场的分布规律

正交水平电偶源和正交水平磁偶源是分别由相互垂直的水平电偶源和相互垂直的水平磁偶源构成,其电磁场的分布也是通过相互垂直的场进行矢量叠加得到的。根据式(5)~(8)和式(18)可以求得水平电偶源均匀半空间的场,同理可求取另一垂直于该源的水平电偶源的场,再利用场的矢量叠加原理求取正交水平电偶源在均匀半空间场的分布规律。同理,利用式(1)~(4)和式(18)获得正交水平磁偶源在均匀半空间场的分布规律。

(18)

\begin{array}{l} \begin{array}{l} E_{x} = E_{ρ} \cdot c o s φ - E_{φ} \cdot s i n φ \\ E_{y} = E_{ρ} \cdot s i n φ + E_{φ} \cdot c o s φ \\ H_{x} = H_{ρ} \cdot c o s φ - H_{φ} \cdot s i n φ \end{array} \\ H_{y} = H_{ρ} \cdot s i n φ + H_{φ} \cdot c o s φ \\ E_{x} = - {E_{y}}^{T}, E_{y} = - {E_{x}}^{T}, H_{x} = {H_{y}}^{T}, H_{y} = {H_{x}}^{T} \end{array}

式中 $E_{x}$ 、 $E_{y}$ 分别为x和y方向的电场水平分量; $H_{x} 、 H_{y}$ 分别为x和y方向的磁场水平分量; ${E_{y}}^{T}$ 、 ${E_{x}}^{T} 、 {H_{x}}^{T}$ 、 ${H_{y}}^{T}$ 分别为 $E_{x}$ , $E_{y}$ , $H_{x}$ , $H_{y}$ 的转置。

考虑到MT的频率范围小于10 kHz,AMT的频率范围小于100 kHz,RMT频率范围大于10 kHz。因此,本文选取为发送频率为10 kHz、100 kHz,均匀半空间(如图1中区域1)电阻率为 $ρ = 100 Ω \cdot m$ 的模型,分别计算了含有位移电流的正交水平电偶源和正交水平磁偶源的电磁场(标量场)分布规律。

2.1.1 正交水平电偶源的电磁场分布规律

在计算包含位移电流下正交水平电偶源场的分布时,如图1所示,正交偶极子的位置位于0 m 处,收发距为 0~1 000 m,水平电偶源极距10 m,发射电流40 A,计算结果取第一象限展示。参考席振铢等^[29]采用数字滤波方法计算汉克尔积分,J₀为61个,J₁为47个,但在RMT的频率范围内,使用此滤波系数计算,误差较大,计算稳定性较差,本文使用Kerry Key^[35]中的滤波系数J₀、J₁均为201个。

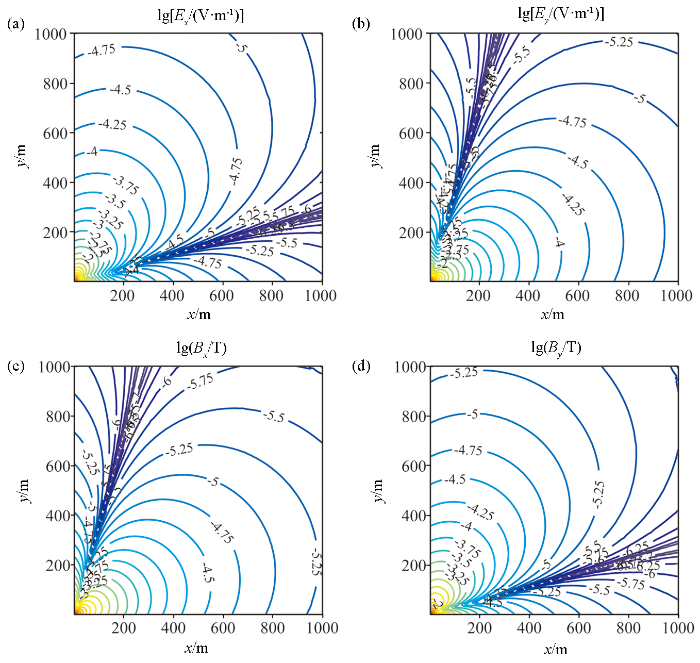
本文电磁场分量采用对数值,图2为考虑位移电流情况下正交水平电偶源发送频率10 kHz电磁场的分布特征。计算结果显示, E_x、B_y场的分布特征相近,E_y、B_x场的分布特征相近,其场的分布存在一条低值带,与忽略位移电流时场的分布^[30]完全一致,因此在发送频率为10 kHz时,可以忽略位移电流进行计算。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 10 kHz水平正交电偶源的电磁场水平分量振幅空间分布示意图

Fig.2 The amplitude of the horizontal component of the electromagnetic field distribution diagram form the orthogonal horizontal electric dipole source with the frequency of 10 kHz

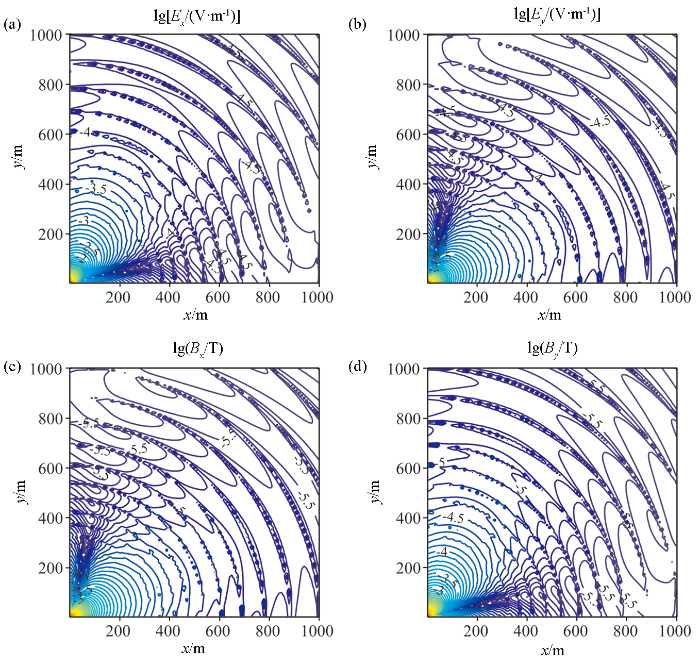
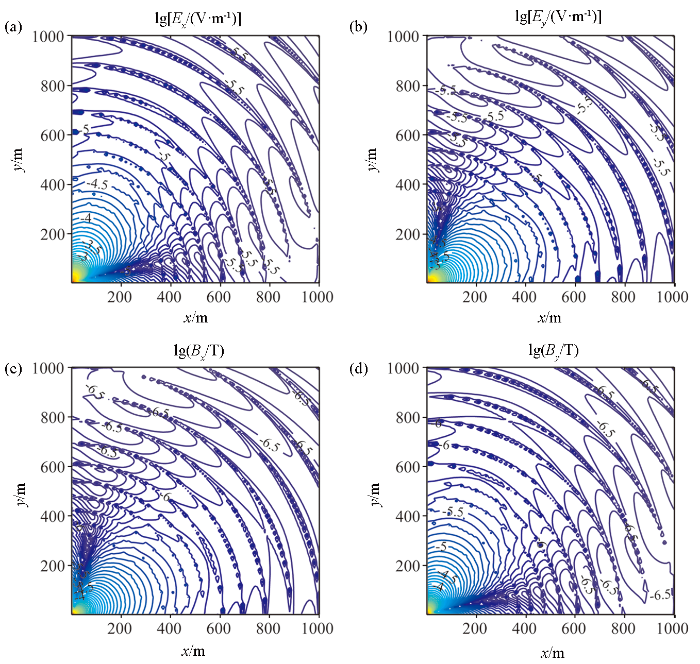
图3为考虑位移电流的正交水平电偶源在发射频率为100 kHz的电磁场分布特征,图中电磁场的分布与忽略位移电流时电磁场的分布^[30]相比趋势相似,但是各方向的场值存在一定程度的震荡,在计算过程中使用不同的J₀、J₁均存在这种震荡,推测这种震荡是由位移电流导致的。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 100 kHz水平正交电偶源的电磁场水平分量振幅空间分布示意图

Fig.3 The amplitude of the horizontal component of the electromagnetic field distribution diagram form the orthogonal horizontal electric dipole source with the frequency of 100 kHz

2.1.2 正交水平磁偶源的电磁场分布规律

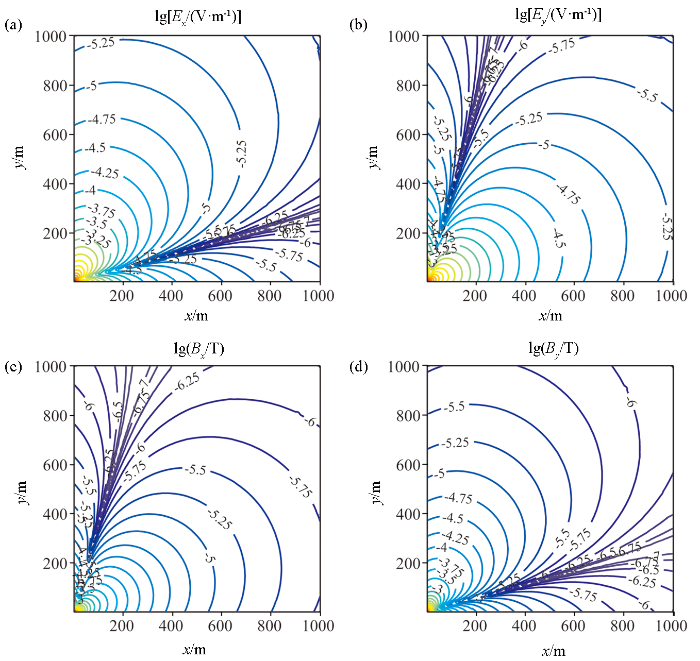
以与2.1.1中相同的模型参数计算考虑位移电流的正交水平磁偶源场的分布,磁偶源的发射磁矩400 Am²。图4为考虑位移电流的正交水平磁偶源发送频率10 kHz电磁场的分布特征,与席振铢^[29]获得的正交水平磁偶源忽略位移电流计算的分布规律一致,图像完全相同。此外,通过图4和图2的对比发现,正交水平磁偶源场的分布规律与正交水平电偶源场的分布规律相似程度较高。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 10 kHz水平正交磁偶源的电磁场水平分量振幅空间分布示意图

Fig.4 The amplitude of the horizontal component of the electromagnetic field distribution diagram form the orthogonal horizontal magnetic dipole source with the frequency of 10 kHz

图5为正交水平磁偶源发送频率100 kHz电磁场的分布特征,电磁场的分布规律在形态上与同频率下的正交水平电偶源整体形态几乎一致,细节上有些许的变化,与正交水平磁偶源在忽略位移电流时计算的结果^[28]在形态轮廓上接近,但电磁场分布上产生了剧烈的波动。当发送频率为100 kHz时,使用不同的J₀、J₁进行计算,这种震荡仍然存在,推测是位移电流对场的分布产生了影响。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 100 kHz水平正交磁偶源的电磁场水平分量振幅空间分布示意图

Fig.5 The amplitude of the horizontal component of the electromagnetic field distribution diagram form the orthogonal horizontal magnetic dipole source with the frequency of 100 kHz

通过上述水平正交电偶源和磁偶源的电磁场水平分量振幅空间分布规律可知,当发送频率大于100 kHz时,位移电流对场分布的影响不可忽略。

2.2 张量视电阻率及阻抗相位的分布

以CSAMT张量阻抗和视电阻率、相位的计算公式(式(19)~(21))为基础,计算包含位移电流的正交水平电偶源和正交水平磁偶源的CSRMT视电阻率和阻抗相位,模型参数如图6所示,其中原点O为发送频率 $f = 100 k H z$ 的正交水平发射源,半空间电阻率为 $ρ = 100 Ω \cdot m$ , $P = \sqrt[]{2} r / δ$ 为感应数( $r$ 为收发距, $δ$ 为趋肤深度),当 $P ≪ 1$ 时为近区, $P ≫ 1$ 时为远区,近区与远区之间的区域为过渡区^[7]。

(19)

\begin{array}{l} Z_{x y} = \frac{E_{x}^{s y} H_{x}^{s x} - E_{x}^{s x} H_{x}^{s y}}{H_{x}^{s x} H_{y}^{s y} - H_{x}^{s y} H_{y}^{s x}}, \\ Z_{y x} = \frac{E_{y}^{s x} H_{y}^{s y} - E_{y}^{s y} H_{y}^{s x}}{H_{x}^{s x} H_{y}^{s y} - H_{x}^{s y} H_{y}^{s x}}, \end{array}

(20)

ρ = \frac{1}{ω μ} {|Z|}^{2}

(21)

φ = a r c t a n \frac{I m (Z)}{R e (Z)}

式中:Z为阻抗, $Z_{x y}$ 、 $Z_{y x}$ 分别为xy方向和yx方向的阻抗; $E_{x}^{s x}$ 、 $E_{y}^{s x}$ 、 $H_{x}^{s x}$ 、 $H_{y}^{s x}$ 分别为x方向的场源产生的x和y方向的电磁场水平分量; $E_{x}^{s y}$ 、 $E_{y}^{s y}$ 、 $H_{x}^{s y}$ 、 $H_{y}^{s y}$ 分别为y方向的场源产生的x和y方向的电磁场水平分量; $μ$ 为介质磁导率。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 CSRMT视电阻率和阻抗相位计算模型

Fig.6 CSRMT apparent resistivity and impedance phase calculation model

2.2.1 正交水平电偶源

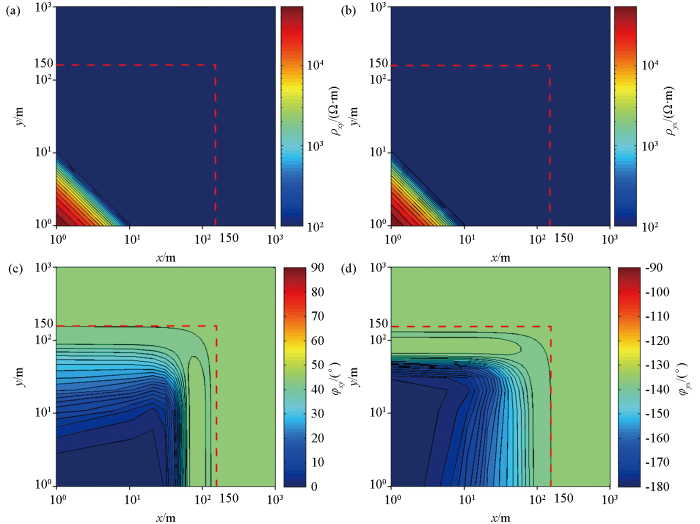
图7为考虑位移电流正交水平电偶源的张量视电阻率和阻抗相位在平面空间的分布情况,在远区时,电阻率值稳定且与均匀空间的电阻率一致,相位分布为45°和-135°(取 $φ_{y x} = φ_{y x} - 180^{°})$ 。现有计算参数条件下,在近区和过渡区的电阻率值范围变化为155~57 000 Ω·m(在源旁边时电阻率最大达57 000 Ω·m),相位也分别接近于0°(φ_xy)和-180°( $φ_{y x}$ )。由图7的结果认为,当观测点位于x轴、y轴、x=150 m和y=150 m(图中红色虚线)组成的正方形之外的区域时,计算得到的电阻率和阻抗相位与均匀空间的一致,因此,应在此正方形之外的位置进行观测。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 100 kHz正交水平电偶源的张量视电阻率和相位空间分布

a—x方向的视电阻率空间分布;b—y方向的视电阻率空间分布;c—x方向的相位空间分布;d—y方向的相位空间分布

Fig.7 Tensor apparent resistivity and phase distribution diagram from the orthogonal horizontal electric dipole source with the frequency of 100 kHz

a—the distribution diagram of apparent resistivity in the x-direction; b—the distribution diagram of apparent resistivity in the y-direction; c—the distribution diagram of phase in the x-direction; d—the distribution diagram of phase in the y-direction

2.2.2 正交水平磁偶源

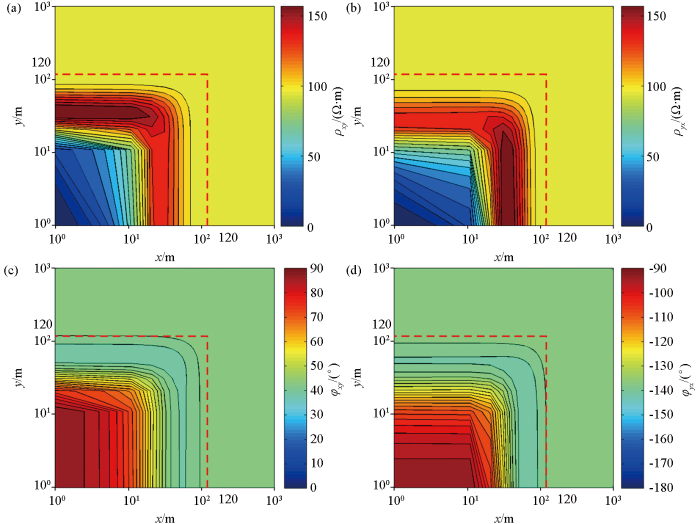
图8为考虑位移电流正交水平磁偶源的张量视电阻率和阻抗相位在平面空间的分布情况图,可以看出在远区时,电阻率值稳定与均匀空间的电阻率一致,相位分布为45°和-135°(对φ_yx-180^°)。在近区和过渡区,张量视电阻率值和相位与正交水平电偶源的相比,变化平缓,电阻率值变化范围为:0.886~164.97 Ω·m,相位 $φ_{x y}$ 变化范围为:80.75°~39.53°,相位 $φ_{y x}$ 变化范围为:-91.26°~137.47°。综合张量视电阻率和阻抗相位的空间分布情况认为,当观测点位于x轴、y轴、x=120 m和y=120 m(图中红色虚线)组成的正方形之外的区域时,计算得到的电阻率和阻抗相位与均匀空间的一致,应在此正方形之外的位置观测。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 100 kHz正交水平磁偶源的张量视电阻率和相位空间分布

a—x方向的视电阻率空间分布;b—y方向的视电阻率空间分布;c—x方向的相位空间分布;d—y方向的相位空间分布

Fig.8 Tensor apparent resistivity and phase distribution diagram from the orthogonal horizontal magnetic dipole source with the frequency of 100 kHz

2.2.3 与忽略位移电流时的误差比较

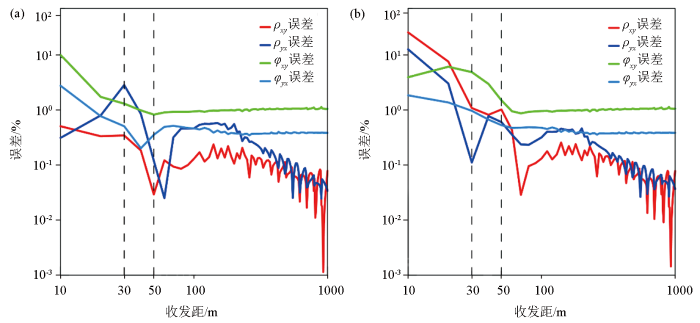
假设半空间电阻率为100 Ω·m,发射频率为10 kHz(位移电流影响可忽略)、100 kHz(位移电流影响不可忽略),收发距从10~1 000 m,计算两者在同样收发距下张量视电阻率和阻抗相位的误差。图9a和图9b分别为正交水平电偶源和正交水平磁偶源下忽略位移电流与考虑位移电流的张量视电阻率和阻抗相位误差随收发距的变化图。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同收发距下正交水平电偶源(a)和磁偶源(b)忽略与包含位移电流的张量视电阻率和阻抗相位误差

Fig.9 The errors of tensor apparent resisvitiy and impedance phase with and without displancement current at differennt separations between transmitter and receiver of the orthogonal horizontal electric dipole source (a) and the orthogonal horizontal magentic dipole source (b)

通过图9可知,忽略位移电流和考虑位移电流的计算结果在收发距小于30 m时,磁偶源的 $ρ_{x y}$ 最大误差达到25.65%, $ρ_{y x}$ 最大误差达到12.63%,其相位的最大误差分别为, $φ_{x y}$ 为6.10%, $φ_{y x}$ 为1.84%;电偶源的 $ρ_{x y}$ 、 $ρ_{y x}$ 误差相对较小,但其相位最大误差分别达到: $φ_{x y}$ 为10.06%, $φ_{y x}$ 为2.76%。超过50 m时,两者的计算结果非常接近,误差基本小于1%,在测量误差范围内,可以忽略不计。因此,在远区进行测量时,若仅计算张量视电阻率和阻抗相位,可以忽略位移电流的影响。

3 收发距和半空间电阻率变化的影响

本节分析电偶源和磁偶源在相同频率时,张量视电阻率和阻抗相位的随收发距变化,以及当均匀半空间电阻率变化时,两种源随不同频率的变化,为野外施工选择源时提供参考。

3.1 收发距对张量视电阻率及相位的对比分析

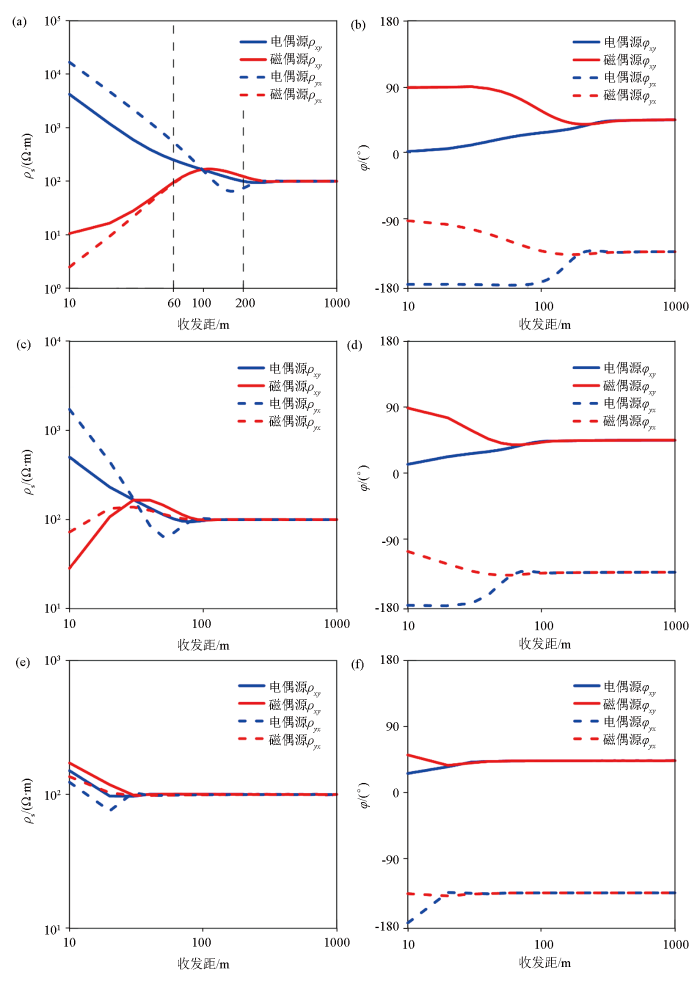
计算参数发送频率分别为f=10、100、1 000 kHz,半空间电阻率为 $ρ = 100 Ω \cdot m$ ,收发距由10~1 000 m变化。图10a~图10b为10 kHz时,张量视电阻率和相位随收发距的变化,图10a显示正交水平电偶源计算的张量视电阻率 $ρ_{x y}$ 在 $>$ 4 000 Ω·m时随收发距的增大而递减,当收发距>200 m后趋于100 Ω·m, 随收发距继续增大而保持稳定, $ρ_{y x}$ 的变化更加剧烈;而正交水平磁偶源 $ρ_{x y}$ 由10 Ω·m慢慢增大,收发距约为100 m时, $ρ_{x y}$ 恢复到100 Ω·m,并随收发距继续增大保持稳定, $ρ_{y x}$ 的变化虽比 $ρ_{x y}$ 变化稍大,但在收发距约为60 m时与 $ρ_{x y}$ 保持一致。两种源阻抗相位 $φ_{x y}$ 与 $φ_{y x}$ 均有一定的变化,为了更好的展示差异性将 $φ_{y x} = φ_{y x} - 180^{°}$ ,最终趋于45°和-135°。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 收发距变化对正交水平电偶源和磁偶源张量视电阻率和相位的影响

a—发送频率10 kHz 对电阻率的影响;b—发送频率10 kHz 对相位的影响;c—发送频率100 kHz对电阻率的影响;d—发送频率100 kHz对相位的影响;e—发送频率1 000 kHz对电阻率的影响;f—发送频率1 000 kHz对相位的影响

Fig.10 Effect of transceiver distance variation on the tensor apparent resistivity and phase of the orthogonal horizontal electric and magnetic dipole sources

a—10 kHz frequency transmit effect on resistivity;b—10 kHz frequency transmit effect on phase;c—100 kHz frequency transmit effect on resistivity;d—100 kHz frequency transmit effect on phase;e—1 000 kHz frequency transmit effect on resistivity;f—1 000 kHz frequency transmit effect on phase

分析图10a、图10c、图10e随着发送频率的增大,进入远区的距离越来越短,因此可以在更小收发距时, $ρ_{x y}$ 和 $ρ_{y x}$ 以及 $φ_{x y}$ 与 $φ_{y x}$ 趋于稳定,并保持不变。同时随着频率的增大 $ρ_{x y}$ 和 $ρ_{y x}$ 变化范围也更靠近半空间的电阻率,对比相位 $φ_{x y}$ 与 $φ_{y x}$ 可知,随着频率的增大正交水平磁偶源比正交水平电偶源变化幅度小。

3.2 不同半空间的对比分析

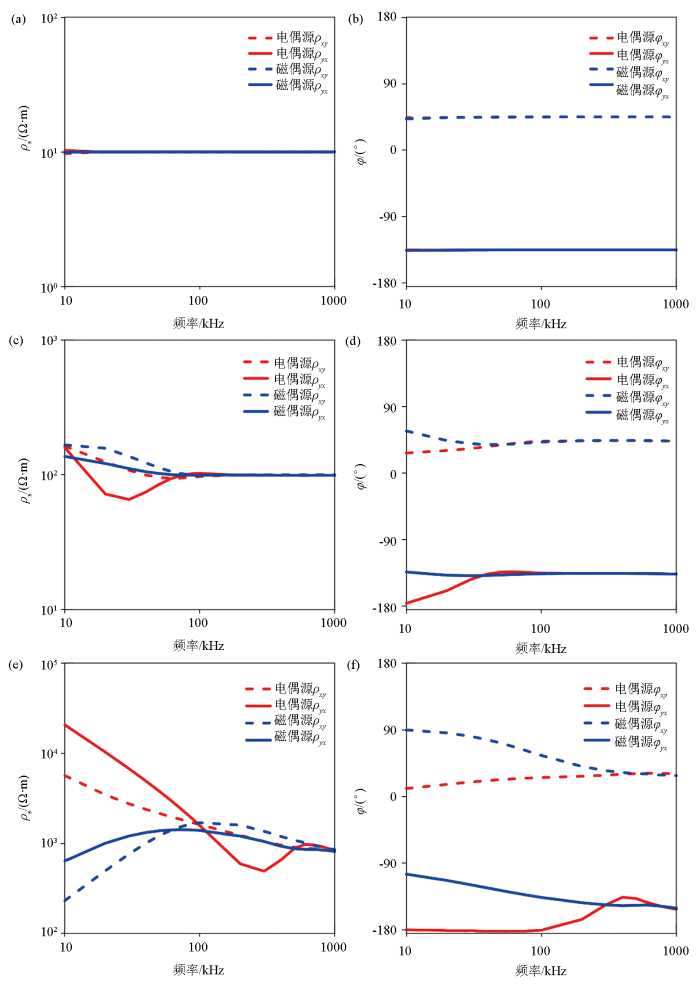
固定收发距为100 m,频率变化范围为10~1 000 kHz,半空间的电阻率范围分别为10、100、1 000 Ω·m时,由图10分析得知,因电阻率保持不变时,频率越低,远区距离越大。从图11a~11f的变化得出,随着半空间电阻率的增大,正交水平电偶源和正交水平磁偶源的视电阻率和阻抗相位会随着频率的增大而趋于稳定,这是由于收发距固定时,在频率较低时,固定的收发距未达到远区要求的距离,但达到远区后正交水平电偶源和正交水平磁偶源的表现均很稳定。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同背景电阻率在正交水平电偶源和磁偶源激励下张量视电阻率和相位随频率的变化

a—背景电阻率为10 Ω·m的视电阻率变化;b—背景电阻率为10 Ω·m的相位变化;c—背景电阻率为100 Ω·m的视电阻率变化;d—背景电阻率为100 Ω·m的相位变化;e—背景电阻率为1 000 Ω·m的视电阻率变化;f—背景电阻率为1 000 Ω·m的相位变化

Fig.11 Variation of tensor apparent resistivity and phase with frequency for different background resistivities under the excitation of the orthogonal horizontal electric and magnetic dipole sources

a—the change of tensor apparent resistivity on the background of 10 Ω·m;b—the change of phase on the background of 10 Ω·m;c—the change of tensor apparent resistivity on the background of 100 Ω·m;d—the change of phase on the background of 100 Ω·m;e—the change of tensor apparent resistivity on the background of 1 000 Ω·m;f—the change of phase on the background of 1 000 Ω·m

由图11a、图11c、图11e的张量视电阻率变化分析可知,随着电阻率的增大,两种源在低频时越震荡,正交水平磁偶源比正交水平电偶源震荡的趋势相对更弱,变化范围更小,相对更加稳定;从图11b、图11d、图11f的阻抗相位变化可以获得相同的结论。

综合分析正交水平电偶源和正交水平磁偶源在收发距和不同电性半空间频率的变化对张量电阻率和阻抗相位影响可知:固定频率的条件下随收发距的变化可知在远区两种源的效果都很好;固定收发距100 m条件下,正交磁偶源的张量电阻率幅值和阻抗相位比正交电偶源的偏差更小;但是实际野外工作中要实现相同大小磁矩的情况下,正交磁偶源的实现比正交电偶源的更难实现,做CSRMT选择源的时候需进行综合考虑。

4 讨论与结论

1)发送频率小于10 kHz时,位移电流对正交水平磁偶源和正交水平电偶源产生的电磁场的影响可以忽略;当发送频率达到100 kHz时,电磁场的分布受到位移电流的影响较大,且在近区时,无论是否考虑位移电流,正交水平电偶源的张量视电阻率变化范围广,畸变严重,而正交水平磁偶源电阻率张量视电阻率变化范围相对较小。

2)通过计算考虑位移电流与忽略位移电流时电磁场的张量视电阻率和相位随收发距的误差发现,在远区时,两者的误差小于1%,几乎可以忽略不计,因此,CSRMT不管发送频率如何,均可以采用准静态场的分析方法。

3)通过计算正交水平磁偶源与正交水平电偶源在频率一致、收发距不同和收发距一定、背景电阻率不同两种情况下的张量电阻率和相位的变化对比分析可知:磁偶源比电偶源的张量视电阻率与相位与实际电阻率和相位偏差相对较小,更有利于分析地质情况。

4)目前计算的视电阻率是卡尼亚电阻率,需要观测两个场分量,后续可继续研究只观测一个场分量的更方便实用的全区视电阻率方法。

附录:

水平磁偶极子电磁场分布公式推导:

如图1设水平磁偶极子平行于x轴,位于(0,0,d)点(图1中d=0),区域1内得水平矢量电位满足非齐次标量亥姆霍兹方程即:

(22)

▽^{2} F_{1 x} + k^{2} F_{1 x} = - \tilde{ε} J_{m}

其解为:

(23)

\begin{array}{l} F_{1 x} = \int_{0}^{\infty} A (λ) e^{- j γ_{1} z} J_{0} (λ ρ) d λ + \tilde{ε} \frac{I_{m} d l}{4 π r_{1}} e^{- j k_{1} r_{1}} = \int_{0}^{\infty} A (λ) e^{- j γ_{1} z} \\ J_{0} (λ ρ) d λ - j {\tilde{ε}}_{1} \frac{I_{m} d l}{4 π} \int_{0}^{\infty} \frac{λ}{γ_{1}} J_{0} (λ ρ) e^{- j γ_{1} |z - d|} d λ \end{array}

区域2内得水平矢量电位:

(24)

▽^{2} F_{2 x} + k^{2} F_{2 x} = 0

其解为:

(25)

F_{2 x} = \int_{0}^{\infty} B (λ) e^{j r_{2} z} J_{0} (λ ρ) d λ

根据磁场切线分量相等,其边界条件为:

(26)

\begin{array}{l} \underset{z \to 0^{+}}{l i m} [F_{j x} + \frac{1}{k_{j}^{2}} \frac{\partial}{\partial x} (\frac{\partial F_{j x}}{\partial x} + \frac{\partial F_{j z}}{\partial z})] = \\ \underset{z \to 0^{-}}{l i m} [F_{i x} + \frac{1}{k_{i}^{2}} \frac{\partial}{\partial x} (\frac{\partial F_{i x}}{\partial x} + \frac{\partial F_{i z}}{\partial z})] \end{array}

(27)

\begin{array}{l} \underset{z \to 0^{+}}{l i m} [\frac{1}{k_{j}^{2}} \frac{\partial}{\partial y} (\frac{\partial F_{j x}}{\partial x} + \frac{\partial F_{j z}}{\partial z})] = \\ \underset{z \to 0^{-}}{l i m} [\frac{1}{k_{i}^{2}} \frac{\partial}{\partial y} (\frac{\partial F_{i x}}{\partial x} + \frac{\partial F_{i z}}{\partial z})] \end{array}

可得:

(28)

A (λ) = j {\tilde{ε}}_{1} \frac{I_{m} d l}{4 π} \frac{λ}{r_{1}} e^{- j r_{1} d} Q

(29)

B (λ) = - j {\tilde{ε}}_{1} \frac{I_{m} d l}{2 π} \frac{λ}{r_{1}} e^{- j r_{1} d} \frac{k_{2}^{2} r_{1}}{N}

式中:

(30)

Q = (k_{1}^{2} r_{2} - k_{2}^{2} r_{1}) / N

(31)

N = k_{1}^{2} r_{2} + k_{2}^{2} r_{1}

区域1和2内得水平矢量电位表达式为:

(32)

F_{1 x} = - j {\tilde{ε}}_{1} \frac{I_{m} d l}{4 π} \int_{0}^{\infty} [e^{- j r_{1} |z - d|} - Q e^{- j r_{1} |z + d|}] \frac{λ}{r_{1}} J_{0} (λ ρ) d λ

(33)

F_{2 x} = - j {\tilde{ε}}_{1} \frac{I_{m} d l}{2 π} \int_{0}^{\infty} e^{j γ_{2} z} e^{- j γ_{1} d} \frac{λ k_{2}^{2}}{N} J_{0} (λ ρ) d λ

$F_{1 x}$ 第一项是水平磁偶极子产生得水平矢量电位,第二项为边界条件产生得矢量电位。

同理带入边界条件可以求取垂直矢量电位为:

(34)

F_{1 z} = - {\tilde{ε}}_{1} \frac{I_{m} d l}{2 π} (k_{1}^{2} - k_{2}^{2}) c o s φ \int_{0}^{\infty} \frac{λ^{2} J_{1} (λ ρ)}{N M} e^{- j γ_{1} (z + d)} d λ

(35)

F_{2 z} = - ε_{0} \frac{I_{m} d l}{2 π} (k_{1}^{2} - k_{2}^{2}) c o s φ \int_{0}^{\infty} \frac{λ^{2} J_{1} (λ ρ)}{N M} e^{j γ_{2} z} e^{- j γ_{1} d} d λ

将矢量位电位式改成3部分的和,增加一个理想负镜像的项,则该式变为:

(36)

F_{1 x} = - j {\tilde{ε}}_{1} \frac{I_{m} d l}{4 π} \int_{0}^{\infty} [e^{- j r_{1} |z - d|} - e^{- j r_{1} |z + d|} + \frac{2 k_{2}^{2} γ_{1}}{N} e^{- j γ_{1} (z + d)}] \frac{λ}{r_{1}} J_{0} (λ ρ) d λ

前两项只需微分运算,即:

(37)

F_{1 x} = {\tilde{ε}}_{1} \frac{I_{m} d l}{4 π} [\frac{e^{- j k_{1} r_{1}}}{r_{1}} - \frac{e^{- j k_{2} r_{2}}}{r_{2}} + 2 j k_{2}^{2} \int_{0}^{\infty} \frac{λ}{N} e^{- j γ_{1} (z + d)} J_{0} (λ ρ) d λ]

则水平矢量电位产生的电磁场分量可表示为:

(38)

\begin{matrix} E_{1 ρ}^{x} = - \frac{I_{m} d l}{4 π} s i n φ [\frac{z - d}{r_{1}} (j \frac{k_{1}}{r_{1}} + \frac{1}{r_{1}^{2}}) e^{- j k_{1} r_{1}} - \frac{z + d}{r_{2}} (j \frac{k_{1}}{r_{2}} + \frac{1}{r_{2}^{2}}) e^{- j k_{1} r_{2}} - 2 k_{2}^{2} \int_{0}^{\infty} \frac{λ γ_{1}}{N} e^{- j r_{1} (z + d)} J_{0} (λ ρ) d λ] \end{matrix}

(39)

\begin{matrix} E_{1 φ}^{x} = - \frac{I_{m} d l}{4 π} c o s φ [\frac{z - d}{r_{1}} (j \frac{k_{1}}{r_{1}} + \frac{1}{r_{1}^{2}}) e^{- j k_{1} r_{1}} - \frac{z + d}{r_{2}} (j \frac{k_{1}}{r_{2}} + \frac{1}{r_{2}^{2}}) e^{- j k_{1} r_{2}} - 2 k_{2}^{2} \int_{0}^{\infty} \frac{λ γ_{1}}{N} e^{- j r_{1} (z + d)} J_{0} (λ ρ) d λ] \end{matrix}

(40)

\begin{array}{l} H_{1 ρ}^{x} = j \frac{I_{m} d l}{4 π ω μ_{0}} c o s φ \{[\frac{k_{1}^{2}}{r_{1}} - j \frac{k_{1}}{r_{1}^{2}} - \frac{1}{r_{1}^{3}} - \frac{ρ^{2}}{r_{1}^{2}} (\frac{k_{1}^{2}}{r_{1}} - j \frac{3 k_{1}}{r_{1}^{2}} - \frac{3}{r_{1}^{3}})] e^{- j k_{1} r_{1}} - \\ [\frac{k_{1}^{2}}{r_{2}} - j \frac{k_{1}}{r_{2}^{2}} - \frac{1}{r_{2}^{3}} - \frac{ρ^{2}}{r_{2}^{2}} (\frac{k_{1}^{2}}{r_{2}} - j \frac{3 k_{1}}{r_{2}^{2}} - \frac{3}{r_{2}^{3}})] e^{- j k_{1} r_{2}} + \\ 2 j k_{2}^{2} [\int_{0}^{\infty} \frac{λ γ_{1}^{2}}{N} e^{- j γ_{1} (z + d)} J_{0} (λ ρ) d λ + \frac{1}{ρ} \int_{0}^{\infty} \frac{λ^{2}}{N} e^{- j γ_{1} (z + d)} J_{1} (λ ρ) d λ]\}, \end{array}

(41)

\begin{array}{l} H_{1 φ}^{x} = - j \frac{I_{m} d l}{4 π ω μ_{0}} s i n φ \{(\frac{k_{1}^{2}}{r_{1}} - j \frac{k_{1}}{r_{1}^{2}} - \frac{1}{r_{1}^{3}}) e^{- j k_{1} r_{1}} - (\frac{k_{1}^{2}}{r_{2}} - j \frac{k_{1}}{r_{2}^{2}} - \frac{1}{r_{2}^{3}}) e^{- j k_{1} r_{2}} + \\ 2 j k_{2}^{2} [k_{1}^{2} \int_{0}^{\infty} \frac{λ}{N} e^{- j γ_{1} (z + d)} J_{0} (λ ρ) d λ - \frac{1}{ρ} \int_{0}^{\infty} \frac{λ^{2}}{N} e^{- j γ_{1} (z + d)} J_{1} (λ ρ) d λ]\}, \end{array}

同理,垂直矢量电位产生的电磁场分量为:

(42)

\begin{matrix} E_{1 ρ}^{z} = - \frac{I_{m} d l}{2 π} \frac{1}{ρ} (k_{1}^{2} - k_{2}^{2}) s i n φ \int_{0}^{\infty} \frac{λ^{2}}{N M} J_{1} (λ ρ) e^{- j γ_{1} (z + d)} d λ \end{matrix}

(43)

E_{1 φ}^{z} = - \frac{I_{m} d l}{2 π} (k_{1}^{2} - k_{2}^{2}) c o s φ \int_{0}^{\infty} \frac{λ^{3}}{N M} [J_{0} (λ ρ) - \frac{J_{1} (λ ρ)}{λ ρ}] e^{- j γ_{1} (z + d)} d λ

(44)

\begin{matrix} H_{1 ρ}^{z} = \frac{I_{m} d l}{2 π ω μ_{0}} (k_{1}^{2} - k_{2}^{2}) c o s φ \int_{0}^{\infty} \frac{λ^{3} γ_{1}}{N M} e^{- j γ_{1} (z + d)} [J_{0} (λ ρ) - \frac{J_{1} (λ ρ)}{λ ρ}] d λ \end{matrix}

(45)

H_{1 φ}^{z} = - \frac{I_{m} d l}{2 π ω μ_{0}} \frac{1}{ρ} (k_{1}^{2} - k_{2}^{2}) s i n φ \int_{0}^{\infty} \frac{λ^{2} γ_{1}}{N M} e^{- j γ_{1} (z + d)} J_{1} (λ ρ) d λ

将水平矢量电位产生的电磁场与垂直矢量电位产生的电磁场进行矢量叠加可得总的电磁场:

(46)

\begin{array}{l} E_{1 ρ} = - \frac{I_{m} d l}{4 π} [s i n φ \frac{z - d}{r_{1}} (j \frac{k_{1}}{r_{1}} + \frac{1}{r_{1}^{2}}) e^{- j k_{1} r_{1}} + \frac{z + d}{r_{2}} (j \frac{k_{1}}{r_{2}} + \frac{1}{r_{2}^{2}}) e^{- j k_{1} r_{2}} + \\ 2 k_{1}^{2} \int_{0}^{\infty} \frac{λ γ_{2}}{N} e^{- j γ_{1} (z + d)} J_{0} (λ ρ) d λ + \frac{2}{ρ} \int_{0}^{\infty} \frac{λ^{2} (γ_{1} - γ_{2})}{N} e^{- j γ_{1} (z + d)} J_{1} (λ ρ) d λ], \end{array}

(47)

\begin{array}{l} E_{1 φ} = - \frac{I_{m} d l}{4 π} c o s φ [\frac{z - d}{r_{1}} (j \frac{k_{1}}{r_{1}} + \frac{1}{r_{1}^{2}}) e^{- j k_{1} r_{1}} + \frac{z + d}{r_{2}} (j \frac{k_{1}}{r_{2}} + \frac{1}{r_{2}^{2}}) e^{- j k_{1} r_{2}} \\ + 2 \int_{0}^{\infty} \frac{λ γ_{1} (γ_{1} γ_{2} + λ^{2})}{N} e^{- j γ_{1} (z + d)} J_{0} (λ ρ) d λ - \frac{2}{ρ} \int_{0}^{\infty} \frac{λ^{2} (γ_{1} - γ_{2})}{N} e^{- j γ_{1} (z + d)} J_{1} (λ ρ) d λ], \end{array}

(48)

\begin{array}{l} H_{1 ρ} = j \frac{I_{m} d l}{4 π ω μ_{0}} c o s φ \{[\frac{k_{1}^{2}}{r_{1}} - j \frac{k_{1}}{r_{1}^{2}} - \frac{1}{r_{1}^{3}} - \frac{ρ^{2}}{r_{1}^{2}} (\frac{k_{1}^{2}}{r_{1}} - j \frac{3 k_{1}}{r_{1}^{2}} - \frac{3}{r_{1}^{3}})] e^{- j k_{1} r_{1}} - \\ [\frac{k_{1}^{2}}{r_{2}} - j \frac{k_{1}}{r_{2}^{2}} - \frac{1}{r_{2}^{3}} - \frac{ρ^{2}}{r_{2}^{2}} (\frac{k_{1}^{2}}{r_{2}} - j \frac{3 k_{1}}{r_{2}^{2}} - \frac{3}{r_{2}^{3}})] e^{- j k_{1} r_{2}} + \\ 2 j \int_{0}^{\infty} \frac{λ γ_{1} γ_{2} (γ_{1} γ_{2} + λ^{2})}{N} e^{- j γ_{1} (z + d)} J_{0} (λ ρ) d λ + j \frac{2}{ρ} \int_{0}^{\infty} \frac{λ^{2} (k_{2}^{2} + {γ_{1}}^{2} - γ_{1} γ_{2})}{N} e^{- j γ_{1} (z + d)} J_{1} (λ ρ) d λ\}, \end{array}

(49)

\begin{array}{l} H_{1 φ} = - j \frac{I_{m} d l}{4 π ω μ_{0}} s i n φ [(\frac{k_{1}^{2}}{r_{1}} - j \frac{k_{1}}{r_{1}^{2}} - \frac{1}{r_{1}^{3}}) e^{- j k_{1} r_{1}} - (\frac{k_{1}^{2}}{r_{2}} - j \frac{k_{1}}{r_{2}^{2}} - \frac{1}{r_{2}^{3}}) e^{- j k_{1} r_{2}} + \\ 2 j k_{1}^{2} k_{2}^{2} \int_{0}^{\infty} \frac{λ}{N} e^{- j γ_{1} (z + d)} J_{0} (λ ρ) d λ - j \frac{2}{ρ} \int_{0}^{\infty} \frac{λ^{2} (k_{2}^{2} + {γ_{1}}^{2} - γ_{1} γ_{2})}{N} e^{- j γ_{1} (z + d)} J_{1} (λ ρ) d λ], \end{array}

将 $d = 0$ 代入式(46)~(49)可得到地面上水平磁偶极子产生的电磁场积分公式。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘钟尹, 陈小斌, 王培杰, 等.

可控射频大地电磁法的野外观测实验和数据处理新技术

[C]// 2021年中国地球科学联合学术年会论文集(七), 2021.