|
|
|
| Moving-footprint-based large-scale model decomposition method for forward modeling of gravity and gravity gradient anomalies |
SHI Ze-Yu1( ), ZHANG Zhi-Hou1,2( ), ZHANG Zhi-Hou1,2( ), LIU Peng-Fei1, FAN Xiang-Tai1 ), LIU Peng-Fei1, FAN Xiang-Tai1 |
1. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China
2. Ministry of Education Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China |
|
|
|
|
Abstract The computational efficiency of the forward modeling for gravity and gravity gradient anomalies determines the feasibility of inverse modeling. It also forms the basis for the efficient building of sufficient and diverse deep learning sample data. Inspired by the application of moving-footprint—a fast forward modeling method in the aerospace electromagnetic field and based on the fast space-domain forward modeling of geometric lattice functions of grid points, the authors proposed a computation method for the forward modeling of gravity and gravity gradient anomalies by applying “moving-footprint”, aiming to further improve the speed of the forward calculation for gravity and gravity gradient anomalies. Specifically, this method selects the subspace in a certain effective range directly below an observation point in the underground half-space. The observation point anomaly approximates the total anomalies of the cuboid units in the corresponding subspace while ignoring the anomalies produced by the cuboid units outside the subspace. When the observation point moves, the corresponding subspace moves accordingly. Therefore, the large-scale underground half-space cuboid model can be decomposed into the subspace corresponding to each calculation point for the forward calculation. As shown by the results of a model test, when 32×32×15 subspace was selected in the underground half-space of a 256×256×15 rectangular parallelepiped model for calculation, the relative average error of gravity anomalies and partial gradient anomalies was less than 10% and the calculation speed was increased by 19 times. Moreover, the calculation time of 1024×1024×15 rectangular parallelepiped model is approximately 32 minutes. Compared with the existing algorithms with a bottleneck in the ultra-conventional calculations, the method proposed in this study has significant advantages regarding computation.
|
|
Received: 24 August 2021
Published: 21 June 2022
|
|
|
|
Corresponding Authors:
ZHANG Zhi-Hou
E-mail: zeyushi2020@163.com;logicprimer@163.com
|
|
|
|
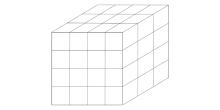
|
Underground half-space unit division
|
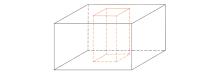
|
Underground grid subspace division schematic diagram
note:the area enclosed by the red line is the subspace
|
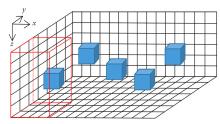
|
Model diagram
note:the area surrounded by the red line is the calculation subspace, and the blue cube is the gravity anomaly area
|

|
256×256 full space operation result
|

|
32×32 subspace operation result
|

|
24×24 subspace operation result
|
|
16×16 subspace operation result
|

| 选取子空间大小 | 运行时间/s | | 16×16 | 151.9600 | | 24×24 | 320.8600 | | 32×32 | 553.1300 | | 256×256 | 10806 |
|
Running time of different subspaces in the whole space
|
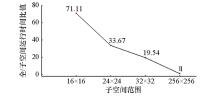
|
Full/subspace operation time ratio
|
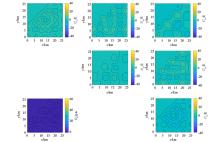
|
256×256 full space and selected calculated 32×32 subspace error
|

| 数据 | U0/(g.u.) | Uxx/E | Uxy/E | Uxz/E | Uyy/E | Uyz/E | Uzz/E | 256×256全空间
勘探结果最大值 | 72.1270 | 17.8441 | 19.0480 | 42.8058 | 17.8441 | 42.8058 | 43.7269 | 256×256全空间
勘探结果最小值 | 0.0896 | -25.1108 | -18.8929 | -42.8058 | -25.1108 | -42.8058 | -10.1804 | 计算值与理论值
误差的均方差 | 0.7175 | 1.2194 | 1.2663 | 0.4103 | 1.2193 | 0.4113 | 0.8841 | 计算值与理论值
误差的均值 | 1.3265 | 0.8269 | 0.0245 | 0.0179 | 0.8327 | -0.0136 | -1.6595 |
|
Maximum and minimum values of gravity and gradient anomalies in full-space calculations Mean and mean square deviation of error between calculated value and theoretical value
|

| 数据 | U0/(g.u.) | Uxx/E | Uxy/E | Uxz/E | Uyy/E | Uyz/E | Uzz/E | | 均方差 | 1.5081 | 1.4733 | 1.2665 | 0.4107 | 1.4765 | 0.4115 | 1.8803 | | 平均相对误差 | 9.01% | 19.90% | 29.09% | 4.76% | 19.94% | 4.77% | 15.47% |
|
The mean square error and average relative error of the 32×32 subspace calculation results
|
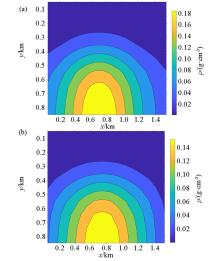
|
Inversion results of different methods in full space 16×16×9
a—the result obtained by the original method;b—the result obtained by applying the Moving-footprint method
|
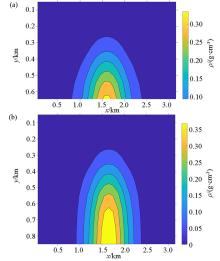
|
Inversion results of different methods in full space 32×32×9
a—the result obtained by the original method;b—the result obtained by applying the Moving-footprint method
|
| [1] |
Hackney R I, Featherstone W E. Geodetic versus geophysical perspectives of the “gravity anomaly”[J]. Geophysical Journal International, 2003, 154(1): 35-43.

|
| [2] |
姚长利, 郝天珧, 管志宁, 等. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报, 2003, 46(2):252-258.
|
| [2] |
Yao C L, Hao T Y, Guan Z N, et al. High-speed computation and efficient storage in 3D gravity and magnetic inversion based on genetic algorithms[J]. Chinese Journal of Geophysics, 2003, 46(2): 252-258.
|
| [3] |
陈召曦, 孟小红, 郭良辉. 重磁数据三维物性反演方法进展[J]. 地球物理学进展, 2012, 27(2):503-511.
|
| [3] |
Chen Z X, Meng X H, Guo L H. Review of 3D property inversion of gravity and magnetic data[J]. Progress in Geophysics, 2012, 27(2): 503-511.
|
| [4] |
张志厚, 廖晓龙, 曹云勇, 等. 基于深度学习的重力异常与重力梯度异常联合反演[J]. 地球物理学报, 2021, 64(4):1435-1452.
|
| [4] |
Zhang Z H, Liao X L, Cao Y Y, et al. Joint gravity and gravity inversion based on deep learning[J]. Chinese Journal of Geophysics, 2021, 64(4): 1435-1452.
|
| [5] |
杨文采, 施志, 侯遵泽, 等. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 2001, 44(4):534-541.
|
| [5] |
Yang W C, Shi Z, Hou Z Z, et al. Discrete wavelet transform and multiple decomposition of gravity anomaly[J]. Chinese Journal of Geophysics, 2001, 44(4): 534-541.
|
| [6] |
Vajda P, Vaníček P, Novák P, et al. Secondary indirect effects in gravity anomaly data inversion or interpretation[J]. Journal of Geophysical Research, 2007, 112(B6):B06411(1-11).
|
| [7] |
Li Y, Oldenburg D W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method[J]. Geophysical Journal International, 2003, 152(2): 251-265.

|
| [8] |
秦朋波, 黄大年. 重力和重力梯度数据联合聚焦反演方法[J]. 地球物理学报, 2016, 59(6):2203-2224.
|
| [8] |
Qin P B, Huang D N. Intergrated gravity and gravity gradient data focusing inversion[J]. Chinese Journal of Geophysics, 2016, 59(6): 2203-2224.
|
| [9] |
熊光楚. 重、磁场三维傅里叶变换的若干问题[J]. 地球物理学报, 1984, 27(1):103-109.
|
| [9] |
Xiong G C. Several problems of three-dimensional Fourier transform of gravity and magnetic field[J]. Chinese Journal of Geophysics, 1984, 27(1): 103-109.
|
| [10] |
Shin Y H, Choi K, Xu H. Three dimensional forward and inverse models for gravity fields based on the Fast Fourier Transform[J]. Computers & Geosciences, 2006, 32(6):27-738.
|
| [11] |
Wu L Y, Tian G. High-precision Fourier forward modeling of potential fields[J]. Geophysics, 2014, 79(5): G59-G68.

|
| [12] |
Ren Z Y, Tang J T, Kalscheuer T, et al. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(1): 79-109.

|
| [13] |
姚长利, 郑元满, 张聿文. 重磁异常三维物性反演随机子域法方法技术[J]. 地球物理学报, 2007, 50(5):1576-1583.
|
| [13] |
Yao C L, Zheng Y M, Zhang Y W. 3-D gravity and magnetic inversion for physical properties using stochastic subspaces[J]. Chinese Journal of Geophysics, 2007, 50(5): 1576-1583.
|
| [14] |
舒晴, 朱晓颖, 周坚鑫, 等. 矩形棱柱体重力梯度张量异常正演计算公式[J]. 物探与化探, 2015, 39(6):1217-1222.
|
| [14] |
Shu Q, Zhu X Y, Zhou J X, et al. Forward calculation formula for the anomaly of gravity gradient tensor of rectangular prism[J]. Physical and Geochemical Exploration, 2015, 39(6): 1217-1222.
|
| [15] |
Cox L H, Wilson G A, Zhdanov M S. 3D inversion of airborne electromagnetic data using a moving footprint[J]. Exploration Geophysics, 2010, 41(4): 250-259.

|
| [16] |
Yin C, Huang X, Liu Y, et al. Footprint for frequency-domain airborne electromagnetic systems[J]. Geophysics, 2014, 79(6): E243-E254.

|
| [1] |
YANG Rong-Xiang, WANG Wan-Yin, CAI Meng-Ke, WANG Ding-Ding, LUO Xin-Gang. A study of tectonic framework of the Qinnan sag in Bohai Basin and its adjacent areas based on satellite gravity anomalies[J]. Geophysical and Geochemical Exploration, 2023, 47(3): 584-596. |
| [2] |
WANG Run-Sheng, WU Bin, ZHANG Hai-Rui, YU Jia-Bin, DONG Yan-Long, GUO Guo-Qiang, KANG Yi-Ming. Gravity field characteristics and boundaries of geotectonic units on the northeastern margin of the Linyi uplift, Shandong Province[J]. Geophysical and Geochemical Exploration, 2023, 47(2): 279-289. |
|
|
|
|

