|
|
|
| VMD-LSTM-based noise detection and predictive reconstruction for magnetotelluric signals |
LI Bo1( ), LI Chang-Wei1,2( ), LI Chang-Wei1,2( ), LUO Run-Lin1,2, LU Yu-Zeng1,2, WANG Zhan1 ), LUO Run-Lin1,2, LU Yu-Zeng1,2, WANG Zhan1 |
1. College of Earth Sciences, Guilin University of Technology, Guilin 541000, China
2. Guangxi Key Laboratory of Exploration for Hidden Metallic Ore Deposits, Guilin 541000, China |
|
|
|
|
Abstract In thereconstruction of actual subsurface structures, strong noise limits the accuracy of the magnetotelluric (MT) method,causing adverse effects on later data interpretation. Given this and the characteristics of the MT time series,this study analyzed different types of noise in the MT time series,proposing a signal denoising technique based on variational mode decomposition (VMD) and long short-term memory (LSTM) predictive reconstruction. First, baseline drift correctionwas performed for the original MT datausing the VMD signal decomposition algorithm. Then, the time series was further decomposed into multiple different intrinsic mode functions (IMFs) through VMD. The LSTM time series detection model was trained using interference-free data in the RSE component, which was then identified. Afterward, the time intervals containing noise weremarked, the increasement of noise was calculated, and the noise information wastransmitted to the original signal for truncation and removal. Finally, an LSTM multi-dimensional prediction model was trained for the IMFs, followed by the prediction of missing values under various modes. The predicted results under all modes were combined to obtain the final predicted MT signals. After signal reconstruction, a secondary signal-noise separationwas performed for spike-pulse noise that was not effectively identified through VMD. TheVMD-LSTM-based signal denoisingtechnique can accurately identify strong noise in MT signals by merely processing the time series intervals containing noise, thuseffectively preserving interference-free data. Moreover, its prediction errors can berestricted within the allowable error range of the data processing for MT signals. Therefore, this technique enjoys significant denoising effects.
|
|
Received: 25 July 2023
Published: 26 February 2025
|
|
|
|
|
|
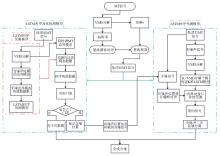
|
Flowchart of the prediction and reconstruction model based on VMD-LSTM
|
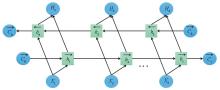
|
Bi-LSTM network architecture diagram
|
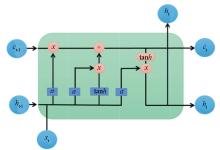
|
LSTM network architecture diagram
|
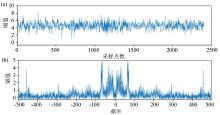
|
Time series graph of the original MT signal(a) and spectrogram of the original MT signal(b)
|

|
Time series graph of the measured signal with added noise(a) and spectrogram of the measured signal with added noise(b)
|

|
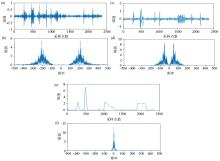
Time series graph and spectrogram of the VMD decomposition for the test signal with K=2
a—IMF1 time series graph;b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram
|
|
Time series graph and spectrogram of the VMD decomposition for the test signal with K=3
a—IMF1 time series graph; b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram;e—IMF3 time series graph;f—IMF3 spectrogram
|
|
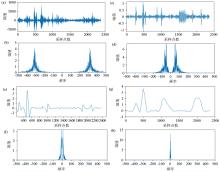
Time series graph and spectrogram of the VMD decomposition for the test signal with K=4
a—IMF1 time series graph;b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram;e—IMF3 time series graph;f—IMF3 spectrogram;g—IMF4 time series graph;h—IMF4 spectrogram
|
|
Time series graph and spectrogram of the VMD decomposition for the test signal with K=5
a—IMF1 time series graph; b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram;e—IMF3 time series graph;f—IMF3 spectrogram;g—IMF4 time series graph;h—IMF4 spectrogram;i—IMF5 time series graph; j—IMF5 spectrogram
|

|
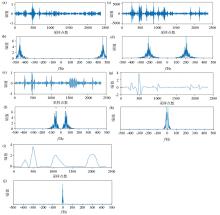
Time series graph and spectrogram of the two components for K=2, under different α values
|
|
Time series graph and spectrogram of the two components for K=2, under different α values
a、e、i、m、q—IMF1 time series graph;b、f、j、n、r—IMF1 spectrogram;c、g、k、o、s—IMF2 time series graph;d、h、l、pt—IMF2 spectrogram
|

|
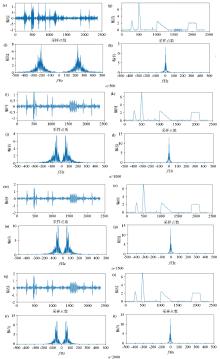
Time-domain spectrogram of the noisy original signal and RES component(a) and frequency spectrum of the noisy original signal and RES component(b)
|

| 数据集 | K值 | α值 | 模型训练个数 | 数据集大小 | | A | 2 | 2000 | 2 | 300×2400×2 | | B | 3 | 2000 | 3 | 300×2400×3 | | C | 4 | 2000 | 4 | 300×2400×4 | | D | 5 | 2000 | 5 | 300×2400×5 | | E | 6 | 2000 | 6 | 300×2400×6 | | F | 7 | 2000 | 7 | 300×2400×7 |
|
Experimental parameters
|

| K值 | 2 | 3 | 4 | 5 | 6 | 7 | | RMSE | 319.684 | 288.3506 | 278.5965 | 242.9843 | 286.9627 | 293.2542 | | MAE | 255.3978 | 177.6701 | 216.9816 | 175.6035 | 219.5106 | 235.4275 | | MAPE | 12.0185% | 11.82071% | 11.4593% | 11.2015% | 11.3134% | 11.5241% | | TIME | 3.1h | 4.4h | 6.5h | 9.8h | 13.2h | 17.6h |
|
Model prediction errors for different values of K
|
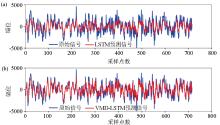
|
Comparison of LSTM predicted signal (a), VMD-LSTM predicted signal (b), and the original signal
|

| 隐含单元数 | 求解器 | 梯度阈值 | 特征维数 | 初始学习率 | 学习因子 | | 128×3 | Adam | 1 | 50 | 0.1 | 0.3 | | 处理器: | AMD RADEON7 5000 SERIES | | | | | | 显卡: | NVIDIA GeForce RTX 3060 | | | | | | 平台: | Matlab2021a | | | | |
|
Experimental parameters and training environment of LSTM model
|
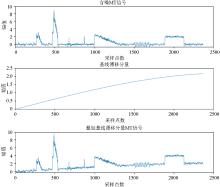
|
Addition of baseline drift component in the noisy MT signal
|
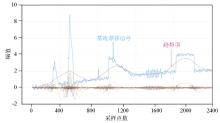
|
VMD decomposition results with controlled α value, K = 20 000
|
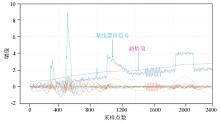
|
VMD decomposition results with controlled K value of 20 000 and gradually increasing α values
|
|
Result of baseline drift processing
|
|
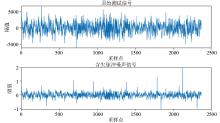
Original test signal with the addition of 10 sharp pulse noises
|
|
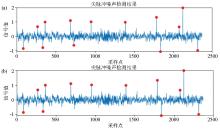
Detection results under different threshold settings
a—threshold set at 90% of the maximum predicted value;b—threshold set at the maximum predicted value
|
|
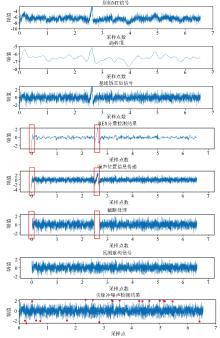
Denoising process of the measured noisy MT signal
|
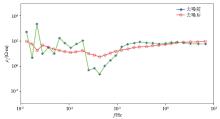
|
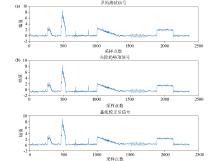
Comparison of apparent resistivity before and after denoising in the measured signal
|
| [1] |
孙洁, 晋光文, 白登海, 等. 大地电磁测深资料的噪声干扰[J]. 物探与化探, 2000, 24(2):119-127.
|
| [1] |
Sun J, Jin G W, Bai D H, et al. The noise interference of magnetotelluric sounding data[J]. Geophysical and Geochemical Exploration, 2000, 24(2):119-127.
|
| [2] |
汤井田, 徐志敏, 肖晓, 等. 庐枞矿集区大地电磁测深强噪声的影响规律[J]. 地球物理学报, 2012, 55(12):4147-4159.
|
| [2] |
Tang J T, Xu Z M, Xiao X, et al. Effect rules of strong noise on magnetotelluric(MT) sounding in the Luzong ore cluster area[J]. Chinese Journal of Geophysics, 2012, 55(12):4147-4159.
|
| [3] |
杨生. 大地电磁测深法环境噪声抑制研究及其应用[D]. 长沙: 中南大学, 2004.
|
| [3] |
Yang S. The study of restraining environmental noise and its application in magnetotelluric sounding[D]. Changsha: Central South University, 2004.
|
| [4] |
汤井田, 化希瑞, 曹哲民, 等. Hilbert-Huang变换与大地电磁噪声压制[J]. 地球物理学报, 2008, 51(2):603-610.
|
| [4] |
Tang J T, Hua X R, Cao Z M, et al. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics, 2008, 51(2):603-610.
|
| [5] |
严家斌, 刘贵忠. 基于小波变换的脉冲类电磁噪声处理[J]. 煤田地质与勘探, 2007, 35(5):61-65.
|
| [5] |
Yan J B, Liu G Z. Like-impulse electromagnetic noise processing based wavelet transform[J]. Coal Geology & Exploration, 2007, 35(5):61-65.
|
| [6] |
李晋. 基于数学形态学的大地电磁强干扰分离及应用[D]. 长沙: 中南大学, 2012.
|
| [6] |
Li J. Magnetotelluric strong interference separationandapplication based on mathematical morphology[D]. Changsha: Central South University, 2012.
|
| [7] |
汤井田, 李广, 肖晓, 等. 基于压缩感知重构算法的大地电磁强干扰分离[J]. 地球物理学报, 2017, 60(9):3642-3654.
|
| [7] |
Tang J T, Li G, Xiao X, et al. Strong noise separation for magnetotelluric data based on a signal reconstruction algorithm of compressivesensing[J]. Chinese Journal of Geophysics, 2017, 60(9):3642-3654.
|
| [8] |
许滔滔, 王中兴, 肖卓伟, 等. 基于LSTM循环神经网络的大地电磁工频干扰压制[J]. 地球物理学进展, 2020, 35(5):2016-2022.
|
| [8] |
Xu T T, Wang Z X, Xiao Z W, et al. Magnetotelluric power frequency interference suppression based on LSTM recurrent neural network[J]. Progress in Geophysics, 2020, 35(5):2016-2022.
|
| [9] |
李德伟, 邓方进, 张召彬. BP神经网络模型预测在大地电磁数据处理中的应用[J]. 科技创新与应用, 2016(24):47-48.
|
| [9] |
Li D W, Deng F J, Zhang Z B. Application of BP neural network model prediction in magnetotelluricdata processing[J]. Technology Innovation and Application, 2016(24):47-48.
|
| [10] |
李炎, 李皓, 钱肖鲁, 等. 异常检测算法分析[J]. 计算机工程, 2002, 28(6):5-6,32.
|
| [10] |
Li Y, Li H, Qian X L, et al. A review and analysis of outlier detection algorithms[J]. Computer Engineering, 2002, 28(6):5-6,32.
|
| [11] |
苏卫星, 朱云龙, 刘芳, 等. 时间序列异常点及突变点的检测算法[J]. 计算机研究与发展, 2014, 51(4):781-788.
|
| [11] |
Su W X, Zhu Y L, Liu F, et al. Outliers and change-points detection algorithm for time series[J]. Journal of Computer Research and Development, 2014, 51(4):781-788.
|
| [12] |
李晋, 张贤, 蔡锦. 利用变分模态分解(VMD)和匹配追踪(MP)联合压制音频大地电磁(AMT)强干扰[J]. 地球物理学报, 2019, 62(10):3866-3884.
|
| [12] |
Li J, Zhang X, Cai J. Suppression of strong interference for AMT using VMD and MP[J]. Chinese Journal of Geophysics, 2019, 62(10):3866-3884.
|
| [13] |
陈斌, 陈松灿, 潘志松, 等. 异常检测综述[J]. 山东大学学报:工学版, 2009, 39(6):13-23.
|
| [13] |
Chen B, Chen S C, Pan Z S, et al. Survey of outlier detection technologies[J]. Journal of Shandong University:Engineering Science, 2009, 39(6):13-23.
|
| [14] |
王岩. 深度神经网络的归一化技术研究[D]. 南京: 南京邮电大学, 2019.
|
| [14] |
Wang Y. Analysis of normalization for deep neural networks[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2019.
|
| [15] |
杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, 38(S2):1-6,26.
|
| [15] |
Yang L, Wu Y Q, Wang J L, et al. A survey of research on circulatory neural network[J]. Journal of Computer Applications, 2018, 38(S2):1-6,26.
|
| [1] |
SHAN Bo, XING Yu-Xin, ZHANG Fan-Chang, LI Zhi-Wei, CHEN Mo. Adaptive prestack inversion method based on quadratic encoder-decoder network[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 158-165. |
| [2] |
ZHAO Li-Fang, YU Si-Yu, LI Shao-Hua. An automatic fitting method for a variogram based on deep learning[J]. Geophysical and Geochemical Exploration, 2024, 48(5): 1359-1367. |
|
|
|
|

