|
|
|
| Application of particle swarm algorithm based on Lévy flight in magnetotelluric inversion |
ZHANG Yang-Yang1( ), DU Wei2( ), DU Wei2( ), WANG Zhi-Shui1, MIAO Xu-Huang1, ZHANG Xiang1 ), WANG Zhi-Shui1, MIAO Xu-Huang1, ZHANG Xiang1 |
1. Geological Exploration Technology Institute of Anhui Province, Hefei 230031, China
2. Yunnan University School of Earth Sciences,Kunming 650091,China |
|
|
|
|
Abstract Particle swarm optimization algorithm has many advantages compared with linear inversion algorithm in magnetotelluric sounding inversion.However, the standard particle swarm algorithm also suffers from premature maturity in multidimensional optimization problems.Therefore, an optimized particle swarm algorithm based on the Lévy flight randomized wandering strategy is used to escape the local optimal solution,The results show that compared with the standard particle swarm optimization algorithm, the optimized particle swarm algorithm has faster fitness decline and better optimization ability.Finally, the improved particle swarm optimization algorithm is applied to the measured data of known boreholes, and the results show that the algorithm has good practicability.
|
|
Received: 30 June 2022
Published: 11 October 2023
|
|
|
|
|
|

|
Schematic diagram of the Lévy flight trajectory after 200 iterations
a—Levy flight path;b—Levy flight step distribution
|
|
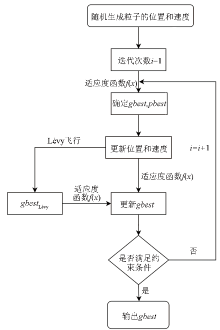
LFPSO algorithm flow chart
|

|
Schematic diagram of variable step FEM element nodes
|
|
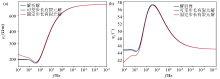
Comparison of forward results of finite element forward modeling with fixed step size and variable step in simple geoelectric model (G type)
a—comparison of apparent resistivity;b—comparison of impedance phase
|

|
Comparison of PSO and LFPSO inversion results and theoretical values of the two-layer geoelectric model
a—G-curve comparison chart;b—D-curve comparison chart;c—the fitness value of G-curve changes iterativel;d—the fitness value of D-curve changes iterativel
|

|
Comparison of PSO and LFPSO inversion results and theoretical values of the three-layer geoelectric model
a—H-curve comparison chart;b—K-curve comparison chart;c—the fitness value of H-curve changes iterativel; d—the fitness value of K-curve changes iterativel
|

|
Inversion results of four different geoelectric models PSO and LFPSO algorithms
|

| 模型参数 | 层号 | | 1 | 2 | 3 | 4 | 5 | 6 | | ρs/(Ω·m) | 100 | 1000 | 10 | 1000 | 10 | 1000 | | 地层厚度/m | 100 | 100 | 50 | 400 | 150 | ∞ |
|
Parameters of six-layer thin-thick interlayer geoelectric model
|
|
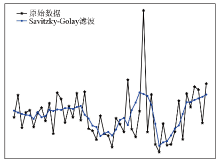
The filtering effect of the filter Savitzky-Golay
|
|
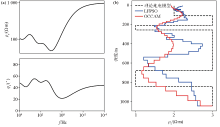
Inversion results of OCCAM inversion and PSO inversion in six-layer geoelectric model
a—finite element forward resistivity and phase curve for the six-layer geoelectric model;b—result of inversion
|
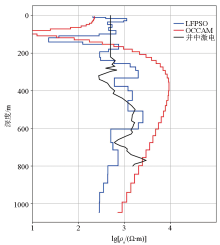
|
Inversion results of measured data at measuring points next to the drill
|
| [1] |
李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2007.
|
| [1] |
Li J M. Geoelectric field and electrical exploration[M]. Beijing: Geology Press, 2007.
|
| [2] |
冯思臣. 一维大地电磁测深反演算法比较研究[D]. 成都: 成都理工大学, 2007.
|
| [2] |
Feng S C. A comparative study of one dimensional magnetotelluric sounding inversion algorithms[D]. Chengdu: Chengdu University of Technology, 2007.
|
| [3] |
石昆法. 可控源音频大地电磁法理论与应用[M]. 北京: 科学出版社, 1999.
|
| [3] |
Shi K F. Theory and application of controlled source audio magnetotelluric method[M]. Beijing: Science Press, 1999.
|
| [4] |
汤井田, 任政勇, 化希瑞. 地球物理学中的电磁场正演与反演[J]. 地球物理学进展, 2007, 22(4):1181-1194.
|
| [4] |
Tang J T, Ren Z Y, Hua X R. The forward modeling and inversion in geophysical electromagnetic field[J]. Progress in Geophysics, 2007, 22(4):1181-1194.
|
| [5] |
王光杰, 王勇, 李帝铨, 等. 基于遗传算法CSAMT反演计算研究[J]. 地球物理学进展, 2016, 21(4):1285-1289.
|
| [5] |
Wang G J, Wang Y, Li D Q, et al. Research on inversion calculation of CSAMT based on genetic algorithm[J]. Progress in Geophysics, 2016, 21(4):1285-1289.
|
| [6] |
孙彩堂, 李玲, 黄维宁, 等. 基于自适应遗传算法的CSAMT一维反演[J]. 石油地球物理勘探, 2017, 52(2):392-397.
|
| [6] |
Sun C T, Li L, Huang W N, et al. One-dimensional inversion of CSAMT based on adaptive genetic algorithm[J]. Oil Geophysical Prospecting, 2017, 52(2):392-397.
|
| [7] |
蒋龙聪, 刘江平. 模拟退火算法及其改进[J]. 工程地球物理学报, 2007, 4(2):135-140.
|
| [7] |
Jiang L C, Liu J P. Revised simulated annealing algorithm[J]. Chinese Journal of Engineering Geophysics, 2007, 4(2):135-140.
|
| [8] |
师学明, 王家映. 一维层状介质大地电磁模拟退火反演法[J]. 地球科学, 1998, 7(5):542-545.
|
| [8] |
Shi X M, Wang J Y. One dimensional magnetotelluric sounding inversion using simulated annealing[J]. Earth Science, 1998, 7(5):542-545.
|
| [9] |
曾志文, 陈晓, 郭冬, 等. 双种群人工蜂群算法及其在MT和重力联合反演中的应用[J]. 石油地球物理勘探, 2021, 56(6):1400-1408.
|
| [9] |
Zeng Z W, Chen X, Guo D, et al. Dual-population artificial bee colony algorithm and its application in joint inversion of magnetotelluric and gravity data[J]. Oil Geophysical Prospecting, 2021, 56(6):1400-1408.
|
| [10] |
谢卓良, 王绪本, 李德伟, 等. 基于混沌天牛群算法的大地电磁反演[J]. 物探化探计算技术, 2022, 44(1):41-50.
|
| [10] |
Xie Z L, Wang X B, Li D W, et al. Magnetotelluric inversion based on chaotic beetle swarm algorithm[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2022, 44(1):41-50.
|
| [11] |
徐正玉, 付能翼, 周洁, 等. 瞬变电磁法非线性优化反演算法对比[J]. 吉林大学学报:地球科学版, 2022, 52(3):744-753.
|
| [11] |
Xu Z Y, Fu N Y, Zhou J, et al. Comparison of nonlinear optimization and inversion algorithms of transient electromagnetic method[J]. Journal of Jilin University:Earth Science Edition, 2022, 52(3):744-753.
|
| [12] |
王一鸣, 宋先海, 张学强. 基于蚁狮优化算法的瑞雷波频散曲线反演[J]. 地质科学通报, 2022, 42(3):331-337.
|
| [12] |
Wang Y M, Song X H, Zhang X Q. Inversion of the dispersion curve of Rayleigh wave based on antlion optimizer algorithm[J]. Bulletin of Geological Science and Technology, 2022, 42(3):331-337.
|
| [13] |
Kennedy J, Eberhart R. Particle swarm optimization[C]// Piscataway: Proceeding of IEEE International Conference on Neural Networks,IEEE CS, 1995:1942-1948.
|
| [14] |
刘建华. 粒子群算法的基本理论及其改进研究[D]. 长沙: 中南大学, 2009.
|
| [14] |
Liu J H. The research of basic theory analysis and imporvement on particle swarm optimization[D]. Changsha: Central South University, 2009.
|
| [15] |
陈先洁, 王绪本, 李德伟, 等. 基于改进粒子群算法的大地电磁阻抗张量分解方法[J]. 物探化探计算技术, 2021, 43(5):620-627.
|
| [15] |
Chen X J, Wang X B, Li D W, et al. Tensor decomposition method of magnetotelluric impedance based on particle swarm optimization[J]. Computing Techniques for Geophysical and Geochemical, 2021, 43(5):620-627.
|
| [16] |
Francesca P, Alessandro S, Alberto G. A review of geophysical modeling based on particle swarm optimization[J]. Surveys in Geophysics, 2021, 42(3):505-549.
|
| [17] |
师学明, 肖敏, 范建柯, 等. 大地电磁阻尼粒子群优化反演法研究[J]. 地球物理学报, 2009, 52(4):1114-1120.
|
| [17] |
Shi X M, Xiao M, Fan J K, et al. The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J]. Chinese Journal of Geophysics, 2009, 52(4):1114-1120.
|
| [18] |
肖敏. 二维大地电磁粒子群优化算法反演方法研究[D]. 武汉: 中国地质大学(武汉), 2011.
|
| [18] |
Xiao M. Research on inversion method of magnetotelluric damped particle swarm optimization[D]. Wuhan: China University of Geosciences(Wuhan), 2011.
|
| [19] |
韩家兴, 吴施楷, 田仁飞, 等. 基于粒子群优化算法的多元线性拟合方法研究及其应用[J]. 物探化探计算技术, 2016, 38(2):212-218.
|
| [19] |
Han J X, Wu S K, Tian R F, et al. The particle swarm optimization research and application based on multivariate linear fitting method[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2016, 38(2):212-218.
|
| [20] |
李明星, 肖林通, 张倚瑞, 等. 瞬变电磁粒子群优化反演研究[J]. 煤炭技术, 2014, 33(9):302-304.
|
| [20] |
Li M X, Xiao L T, Zhang Y R, et al. Research on particle swarm optimization inversion of transient electromagnetic method[J]. Coal Technology, 2014, 33(9):302-304.
|
| [21] |
Kennedy J. The particle swarm:social adaptation of knowledge[C]// Indianapolis: IEEE International Conference on Evolutionary Computation, 1997.
|
| [22] |
Mantegna R N. Fast,accurate algorithm for numerical simulation of Lévy stable stochastic processes[J]. Physical Review E, 1994, 49(5):4677.

|
| [23] |
吴小平, 徐果明. 大地电磁数据的Occam反演改进[J]. 地球物理学报, 1998, 41(4):547-554.
|
| [23] |
Wu X P, Xu G M. Improvement of Occam’s inversion for MT data[J]. Chinese Journal of Geophysics, 1998, 41(4):547-554.
|
| [24] |
吴小平, 徐果明, 卫山, 等. 利用新的MT视电阻率定义识别薄互层[J]. 石油地球物理勘探, 1998, 33(3):328-335.
|
| [24] |
Wu X P, Xu G M, Wei S, et al. Defining and identifying thin interbeds by using new MT apparent resistivity[J]. Oil Geophysical Prospecting, 1998, 33(3):328-335.
|
| [25] |
梁生贤, 吾守艾力·肉孜, 廖国忠, 等. 大地电磁线性反演算法比较[J]. 地球物理学进展, 2014, 29(6):2702-2707.
|
| [25] |
Liang S X, Wu-shou-ai-li·R Z, Liao G Z, et al. Comparison and analysis of two-dimensional linear algorithm inversion for magnetoteluric[J]. Progres in Geophysics, 2014, 29(6):2702-2707.
|
|
|
|

