|
|
|
| One-dimensional inversion of induced polarization sounding data based on the differential evolution algorithm with two-step mutation |
DING Zhi-Jun1( ), LUO Wei-Bin2( ), LUO Wei-Bin2( ), LIAN Wei-Zhang1, ZHANG Xing1, HE Hai-Pin2 ), LIAN Wei-Zhang1, ZHANG Xing1, HE Hai-Pin2 |
1. Gansu Nonferrous Geological Survey Institute, Lanzhou 730000, China
2. Lanzhou Resources and Environment Vocational and Technical University, College of Geology and Jewelry, Lanzhou 730021, China |
|
|
|
|
Abstract The one-dimensional inversion of induced polarization (IP) sounding data involves multi-parameter nonlinear optimization. This study achieved the one-dimensional (1D) inversion of IP sounding data based on the improved global optimization algorithm of differential evolution (DE) with two-step mutation. The conventional DE algorithm includes mutation (single-step), crossover, and selection operations. The two-step mutation method proposed in this study can produce new individuals through the mutation of the optimal individual and two randomly selected individuals in steps, thus enhancing the influence of the optimal individual and the global optimization ability. The model test results show that the two-step mutation method has a higher optimization ability than the conventional method. Specifically, the polarizability parameters were loaded using the equivalent resistivity method, and the surface IP sounding resistivity curves of a layered model can be quickly calculated through forward modeling using the digital filtering algorithm. Based on this, the DE algorithm with two-step mutation was employed to produce new individuals through continuous mutation. Then, the resistivity obtained through forward modeling was fitted with the observed values, and the individuals whose fitness approached the maximum fitness were selected as the inversion results. The inversion method proposed in this study features simple operations and fast calculations. As verified through the calculations of H- and KH-type geoelectric models, the inversion method enjoys high fitting accuracy.
|
|
Received: 15 February 2023
Published: 11 October 2023
|
|
|
|
|
|
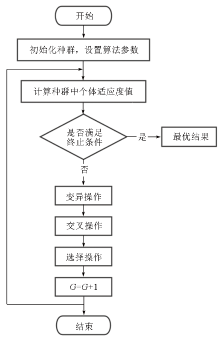
|
Flow chart of differential evolution
|

|
Flow chart of two-step variation method
|

| 模型参数 | 真值 | 取值范围 | 反演次数 | 均值 | 误差/% | | 1 | 2 | 3 | 4 | 5 | | ρ1/(Ω·m) | 100 | [10,300] | 99.72 | 99.50 | 99.78 | 99.50 | 100.32 | 99.76 | -0.24 | | ρ2/(Ω·m) | 30 | [10,150] | 31.15 | 29.93 | 31.80 | 30.09 | 30.31 | 30.66 | 2.19 | | ρ3/(Ω·m) | 110 | [10,300] | 110.56 | 110.56 | 107.63 | 107.27 | 107.34 | 108.67 | -1.21 | | d1/m | 180 | [10,300] | 180.00 | 180.00 | 180.00 | 180.00 | 180.00 | 180.00 | 0.00 | | d2/m | 60 | [10,300] | 59.99 | 60.01 | 59.99 | 60.01 | 60.00 | 60.00 | 0.00 | | η1/m | 0.5 | [0.1, 1] | 0.78 | 1.00 | 0.72 | 1.00 | 0.18 | 0.74 | 0.24 | | η2/m | 8.5 | [3, 11] | 4.97 | 8.72 | 3.00 | 8.24 | 7.56 | 6.50 | -2.00 | | η3/m | 1 | [0.5, 3.5] | 0.50 | 0.50 | 3.13 | 3.46 | 3.40 | 2.20 | 1.20 |
|
Parameters and inversion results of H-type earth resistivity model
|
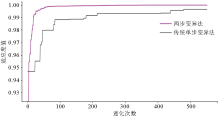
|
Performance comparison between traditional differential evolution and two-step mutation differential evolution
|
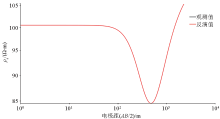
|
Comparison of resistivity sounding results between real model and inversion results of H-type model
|

| 模型参数 | 真值 | 取值范围 | 反演次数 | 均值 | 误差/% | | 1 | 2 | 3 | 4 | 5 | | ρ1/(Ω·m) | 120 | [10,300] | 119.52 | 120.24 | 120.39 | 120.48 | 120.47 | 120.22 | 0.18 | | ρ2/(Ω·m) | 560 | [100,800] | 557.21 | 557.26 | 559.88 | 559.71 | 557.59 | 558.33 | -0.30 | | ρ3/(Ω·m) | 25 | [10,100] | 26.04 | 26.85 | 26.10 | 24.37 | 24.32 | 25.53 | 2.14 | | ρ4/(Ω·m) | 310 | [50,500] | 310.58 | 306.77 | 303.68 | 304.13 | 310.54 | 307.14 | -0.92 | | d1/m | 110 | [50,300] | 110.00 | 110.00 | 110.04 | 110.00 | 110.00 | 110.01 | 0.01 | | d2/m | 120 | [50,300] | 120.00 | 119.98 | 119.20 | 119.98 | 120.02 | 119.83 | -0.14 | | d3/m | 150 | [50,300] | 150.03 | 150.29 | 160.59 | 150.31 | 149.68 | 152.18 | 1.45 | | η1/m | 0.6 | [0.2,1] | 1.00 | 0.40 | 0.28 | 0.20 | 0.21 | 0.42 | -0.18 | | η2/m | 0.3 | [0.1,0.8] | 0.80 | 0.80 | 0.65 | 0.36 | 0.72 | 0.67 | 0.37 | | η3/m | 9.5 | [3,12] | 5.76 | 3.00 | 11.59 | 11.95 | 11.80 | 8.82 | -0.68 | | η4/m | 1 | [0.8,3.5] | 0.81 | 2.03 | 3.08 | 2.88 | 0.82 | 1.93 | 0.93 |
|
Parameters and inversion results of KH-type earth resistivity model
|
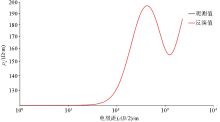
|
Comparison of resistivity sounding results between real model and inversion results of KH-type model
|
| [1] |
李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2005.
|
| [1] |
Li J M. Geoelectric field and electrical prospecting[M]. Beijing: Geology Press, 2005.
|
| [2] |
何继善. 双频激电法[M]. 北京: 高等教育出版社, 2006.
|
| [2] |
He J S. Dual frequency induced polarization method[M]. Beijing: Higher Education Press, 2006.
|
| [3] |
Zhdanov M S. Foundations of geophysical electromagnetic theory and methods[J]. Current Science, 2018, 115(7):1399-1400.
|
| [4] |
刘海飞, 柳建新, 刘嵘, 等. 激发极化法在有色金属矿产勘查中的研究进展[J]. 中国有色金属学报, 2022, 33(1):203-222.
|
| [4] |
Liu H F, Liu J X, Liu R, et al. Research proqress of induced polarization method in nonferrous metal mineral exploration[J]. The Chinese Journal of Nonferrous Metals, 2023, 33(1):203-222.
|
| [5] |
陈儒军, 刘春明, 何兰芳, 等. 阵列式扩频激电法关键技术研究及应用[R]. 中国有色金属工业协会, 2020.
|
| [5] |
Chen R J, Liu C M, He L F, et al. Key technology research and application of array spread spectrum induced polarization method[R]. China Nonferrous Metals Industry Association, 2020.
|
| [6] |
潘北斗. 内蒙古东乌旗地区激发极化法精细化反演方法研究[J]. 物探化探计算技术, 2022, 44 (4):459-467.
|
| [6] |
Pan B D. Research on fine inversion method of induced polarization method in Dongwuqi Area,Inner Mongolia[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2022, 44 (4):459-467
|
| [7] |
师学明, 王家映. 地球物理资料非线性反演方法讲座(四)—遗传算法[J]. 工程地球物理学报, 2008, 5(2):129-140.
|
| [7] |
Shi X M, Wang J Y. Lecture on nonlinear inversion methods of geophysical data (IV)—Genetic algorithm[J]. Journal of Engineering Geophysics, 2008, 5(2):129-140

|
| [8] |
刘宇. 基于卷积神经网络的污染场地电阻率与极化率反演[D]. 上海: 上海应用技术大学, 2021.
|
| [8] |
Liu Y. Resistivity and polarizability inversion of pollution sites based on convolutional neural network[D]. Shanghai: Shanghai Institute of Technology, 2021.
|
| [9] |
王天意, 侯征, 何元勋. 基于改进差分进化算法的大地电磁反演[J]. 地球物理学进展, 2022, 37(4):1605-1612.
|
| [9] |
Wang T Y, Hou Z, He Y X, et al. Magnetotelluric inversion based on the improved differential evolution algorithm[J]. Progress in Geophysics, 2022, 37(4):1605-1612.
|
| [10] |
Mykel J K, Tim A W. Algorithms for optimization[M]. Cambridge: The MIT Press, 2019.
|
| [11] |
高颖, 夏斌, 张立晔, 等. 差分进化协同定位算法的研究[J/OL]. 无线电工程, http://kns.cnki.net/kcms/detail//13.1097.TN.202301117.1402.002.html
|
| [11] |
Gao Y, Xia B, Zhang L Y, et al. Differential evolution cooperative localization algorithm[J/OL]. Radio Engineering, http://kns.cnki.net/kcms/detail//13.1097.TN.202301117.1402.002.html
|
| [12] |
闫秀英, 许成炎. 基于改进DEPSO算法的冷水机组负荷优化方法[J]. 控制工程, 2022, 29(12):2194-2203.
|
| [12] |
Yan X Y, Xu C Y. Optimization method of chiller loading based on improved DEPSO algorithm[J]. Control Engineering of China, 2022, 29(12):2194-2203.
|
| [13] |
丁学振, 李卓轩, 李予国, 等. 基于差分进化算法的磁梯度张量系统误差校正[J]. 地球物理学报, 2022, 65(12):4930-4943.
|
| [13] |
Ding X Z, Li Z X, Li Y G, et al. Calibration of magnetic gradient tensor system with differential evolution algorithm[J]. Chinese Journal of Geophysics, 2022, 65(12):4930-4943.
|
| [14] |
廖作文. 基于差分进化算法的非线性方程组多根联解研究[D]. 武汉: 中国地质大学(武汉), 2019.
|
| [14] |
Liao Z W. Simultaneously locating multiple roots of nonlinear equations based on differential evolution[D]. Wuhan: China University of Geosciences(Wuhan), 2019.
|
| [15] |
王紫郡, 刘云, 吴夏涛, 等. 带装置系数的一维电测深数值模拟方法[J]. 物探化探计算技术, 2022, 44(5):590-596.
|
| [15] |
Wang Z J, Liu Y, Wu X T, et al. A calculation of apparent resistivity with device coefficient in 1D resistivity sounding[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2022, 44 (5):590-596.
|
| [16] |
Ghosh D P. Inverse filter coefficients for the computation of apparent resistivity standard curves for a horizontally stratified earth[J]. Geophysical Prospecting, 1971, 19(4):769-775.

|
| [17] |
Guptasarma D. Optimization of short digital linear filters for increased accuracy[J]. Geophysical Prospecting, 1982, 30(4):501-504.

|
| [18] |
刘金琨, 沈晓蓉, 赵龙. 系统辨识理论及MATLAB仿真(第2版)[M]. 北京: 电子工业出版社, 2020.
|
| [18] |
Liu J K, Shen X R, Zhao L. System identification theory and MATLAB simulation (2nd Edition)[M]. Beijing: Electronic Industry Press, 2020.
|
| [19] |
邓峻, 魏文红, 张宇辉, 等. 基于三种群演化策略的自适应差分进化算法[J]. 东莞理工学院学报, 2022, 29(1):60-66,76.
|
| [19] |
Deng J, Wei W H, Zhang Y H, et al. Adaptive differential evolution algorithm based on three population evolution strategy[J]. Journal of Dongguan University of Technology, 2022, 29(1):60-66,76.
|
| [1] |
YOU Xi-Ran, ZHANG Ji-Feng, SHI Yu. Artificial neural network-based transient electromagnetic imaging[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1206-1214. |
| [2] |
HE Sheng, WANG Wan-Ping, DONG Gao-Feng, NAN Xiu-Jia, WEI Feng-Feng, BAI Yong-Yong. Application of the opposing-coils transient electromagnetic method in urban geological surveys[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1379-1386. |
|
|
|
|

