|
|
|
| A comparative study of Mur second-order absorbing boundary condition and unsplit recursive convolutional perfectly matched layer method under multi-source concurrency |
CUI Fan1,2( ), CHEN Yi1( ), CHEN Yi1( ), XUE Han-Peng1, PENG Su-Ping1,2, DU Yun-Fei1 ), XUE Han-Peng1, PENG Su-Ping1,2, DU Yun-Fei1 |
1. School of Geosciences and Surveying Engineering,China University of Mining and Technology(Beijing),Beijing 100083,China
2. State Key Laboratory of Coal Resources and Safe Mining,China University of Mining and Technology(Beijing),Beijing 100083,China |
|
|
|
|
Abstract Plane beam signals form when multiple excitation sources simultaneously emit pulses with the same center frequency (multiple-source concurrency),thus enhancing the quality of data records.This paper compares and analyzes the electromagnetic wave absorption effects of unsplit recursive convolutional perfectly matched layer (PML) as the absorbing boundary condition and Mur second-order absorbing boundary condition under multi-source concurrency through numerical simulation.According to study results,the traditional Mur second-order absorbing boundary condition did not perform well in absorbing electromagnetic waves under the conditions of multi-source concurrency and multi-angle grazing,and it will cause waveform distortion and spurious reflections in the case of large offsets.For the unsplit recursive convolutional perfectly matched layer as the absorbing boundary condition under multi-source concurrency,coordinate scale factors were introduced into the finite-difference time-domain (FDTD) algorithm.Then,the PML equation for coordinate stretching was transformed from frequency domain into time domain through the inverse Fourier transform.Finally,the electric and magnetic field values were solved using the recursive convolution method in the discrete state,thus avoiding the complicated calculation involved in directly determining the numerical solution of convolution.This allows less memory space and high calculation efficiency while ensuring accuracy.Therefore,the unsplit recursive convolutional perfectly matched layer method improves the electromagnetic wave absorption effect at the positions where the grid terminate without inducing wave-field splitting.
|
|
Received: 12 April 2021
Published: 21 June 2022
|
|
|
|
Corresponding Authors:
CHEN Yi
E-mail: cuifan_cumtb@126.com;cy18729242764@163.com
|
|
|
|
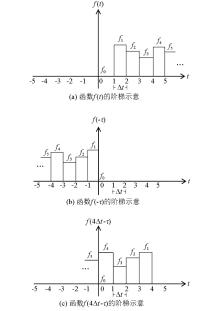
|
Stepped representation of function f(t)
|
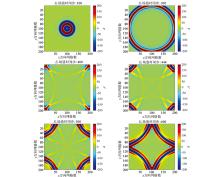
|
Ez wave field at different time steps of uncorrected corners
|
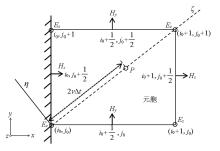
|
Schematic diagram of TM wave lower left corner correction
|

|
Snapshots of Ez wave field at different time steps of the homogeneous medium recursive convolution perfectly matched layer
|
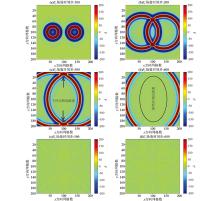
|
Snapshots of Ez wave field at different time steps of Mur second-order absorbing boundary in homogeneous medium
|
|
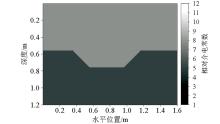
Schematic diagram of low-lying model structure
|
|
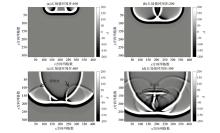
Snapshots of the Ez wave field of the low-lying model at different time steps
|

|
Snapshot of the low-lying model at 700 time step Ez wave field
a—recursive convolution complete matching layer wave field snapshot;b—snapshot of Mur second-order absorbing boundary wave field
|

|
Multi-source concurrent radar data recording
a—recursive convolution complete matching layer data record;b—Mur second-order absorbing boundary data record
|

|
Single excitation source radar data record
a—recursive convolution complete matching layer data record;b—Mur second-order absorbing boundary data record
|
| [1] |
Bayliss A, Turkel E. Radiation boundary conditions for wave-like equations[J]. Communications on Pure and Applied Mathematics, 1980, 33(6):707-725.
|
| [2] |
Engquist B, Majda A. Absorbing boundary conditions for numerical simulation of waves[J]. Proceedings of the National Academy of Sciences of the United States of America, 1977, 74(5):1765-1766.
|
| [3] |
Mur G. Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations[J]. IEEE Transactions on Electromagnetic Compatibility, 1981, 23(4):377-382.
|
| [4] |
Berenger J P. Three-dimensional perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1996, 127(2):363-379.
|
| [5] |
Chen Y H, Weng C C, Oristagilo M L. Application of perfectly matched layers to the transient modeling of subsurface EM problems[J]. Geophysics, 1997, 97(6):1730-1736.
|
| [6] |
Festa G. Interaction between surface waves and absorbing boundaries for wave propagation in geological basins:2D numerical simulations[J]. Geophysical Research Letters, 2005, 32:L20306.
|
| [7] |
Qin Z, Lu M, Zheng X, et al. The implementation of an improved NPML absorbing boundary condition in elastic wave modeling[J]. Applied Geophysics, 2009, 6(2):113-121.
|
| [8] |
Higdon R L. Absorbing boundary conditions for elastic waves[J]. Siam Journal on Numerical Analysis, 2012, 31(2):64-100.
|
| [9] |
Liao Z P, Wong H L, Yang B P, et al. A transmitting boundary for transient wave analysis[J]. Science in China Series A-Mathematics Physics Astronomy & Technological Science, 1984, 27(10):1063-1076.
|
| [10] |
Marfurt K J. Accuracy of finite difference and finite element modeling of the scalar and elastic wave equation[J]. Geophysics, 1984, 49(4):533-549.
|
| [11] |
丁科. PML吸收边界条件影响因素分析[J]. 物探与化探, 2012, 36(4):623-627.
|
| [11] |
Ding K. Analysis of influencing factors of PML absorption boundary conditions[J]. Geophysical and Geochemical Exploration, 2012, 36(4):623-627.
|
| [12] |
Sacks S Z, Kingsland M D, Lee R, et al. A perfectly matched anisotropic absorber for use as an absorbing boundary condition[J]. IEEE Transactions on Antennas & Propagation, 1995, 43(12):1460-1463.
|
| [13] |
Gedney D S. An anisotropic perfectly matched layer-absorbing medium for the truncation of FDTD lattices[J]. IEEE Transactions on Antennas & Propagation, 2002, 44(12):1630-1639.
|
| [14] |
肖明顺, 昌彦君, 曹中林, 等. 探地雷达数值模拟的吸收边界条件研究[J]. 工程地球物理学报, 2008, 5(3):315-320.
|
| [14] |
Xiao M S, Chang Y J, Cao Z L, et al. Study on absorption boundary conditions for numerical simulation of ground penetrating radar[J]. Journal of Engineering Geophysics, 2008, 5(3):315-320.
|
| [15] |
詹应林, 昌彦君, 曹中林. 基于UPML吸收边界的探地雷达数值模拟研究[J]. 资源环境与工程, 2008, 22(2):235-238.
|
| [15] |
Zhan Y L, Chang Y J, Cao Z L. Numerical simulation of ground penetrating radar based on UPML absorption boundary[J]. Resources Environment and Engineering, 2008, 22(2):235-238.
|
| [16] |
冯德山, 谢源. 基于单轴各向异性完全匹配层边界条件的ADI-FDTD三维GPR全波场正演[J]. 中南大学学报:自然科学版, 2011, 42(8):202-210.
|
| [16] |
Feng D S, Xie Y. Full Wave field forward modeling of 3D GPR based on boundary conditions of uniaxial anisotropic completely matched layer[J]. Journal of Central South University:Science and Technology, 2011, 42(8):202-210.
|
| [17] |
冯德山, 陈承申, 戴前伟. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟[J]. 地球物理学报, 2010, 53(10):2484-2496.
|
| [17] |
Feng D S, Chen C S, Dai Q W. Numerical simulation of GPR full wave field with alternate direction implicit finite difference method based on UPML boundary condition[J]. Chinese Journal of Geophysics, 2010, 53(10):2484-2496.
|
| [18] |
冯德山, 王向宇. 基于卷积完全匹配层的旋转交错网格高阶差分法模拟弹性波传播[J]. 物探与化探, 2018, 42(4):766-776.
|
| [18] |
Feng D S, Wang X Y. Elastic wave propagation simulation in anisotropic media and random media using heig-order difference method of rotation staggered grids based on convolutional perfectly matched layer[J]. Geophysical and Geochemical Exploration, 2018, 42(4):766-776.
|
| [19] |
李静, 曾昭发, 吴丰收, 等. 探地雷达三维高阶时域有限差分法模拟研究[J]. 地球物理学报, 2010, 53(4):974-981.
|
| [19] |
LI J, Zeng Z F, Wu F S, et al. Study of three dimension high-order FDTD simulation for GPR[J]. Chinese Journal of Geophysics, 2010, 53(4):974-981.
|
| [20] |
Chew W C, Weedon W H. A 3D perfectly matched medium from modified maxwell’s equations with stretched coordinates[J]. Microwave & Optical Technology Letters, 2010, 7(13):599-604.
|
| [21] |
Kuzuoglu M, Mittra R. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers[J]. IEEE Microwave & Guided Wave Lett, 1996, 6(12):447-449.
|
|
|
|

