|
|
|
| The prediction method of in-situ stress based on pre-stack anisotropic parameter inversion |
| Chao WANG1, Wei-Qi SONG1, Yu-Han LIN1, Yun-Yin ZHANG2, Qiu-Ju GAO2, Xin-Wei WEI2 |
1. College of Earth Science and Technology,China University of Petroleum(East China),Qingdao 266580,China
2. Institute of Geophysical Exploration,Shengli Oilfield Company,Sinopec,Dongying 257000,China |
|
|
|
|
Abstract In the exploration and development of oil and gas reservoirs,the in-situ stress is closely related to the distribution of fractures,while fracture is an important channel for migration and accumulation of oil and gas,so the study of in-situ stress is of great significance for oil and gas development.In this paper,tight sandstone was taken as the research object.On the basis of the transverse isotropic rock layer model and in consideration of the complexity of sand and mud layer stress changes,the formation was assumed to be orthotropic,the elastic parameters of the inverse elastic impedance were taken as the background field of the working area,then the anisotropic parameters in orthotropic medium were obtained,and the ratio of differential stresses was calculated.The anisotropic impedance equation was used in this study,and the elastic parameters and fracture flexibility parameters were converted into anisotropic parameters,in order to verify the accuracy of the prediction method for the in-situ stress of tight sandstone;the ratio of differential stress calculated under the orthotropic model was compared with the results of the same log calculation and various characterization methods.It is shown that the results of geostress calculated under the assumption of orthogonal medium model are basically the same as those calculated by various control methods,thus proving that the orthotropic model stress prediction method is applicable in sand and mudstone formations,and has a good guiding significance for the exploration and development of low permeability oil and gas reservoirs in the future.
|
|
Received: 29 March 2019
Published: 03 March 2020
|
|
|
|
|
|
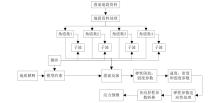
|
Flow chart of stress prediction
|

|
Inversion results are processed
|
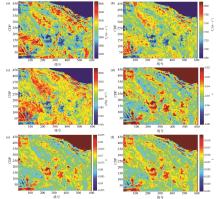
|
Slice sections of elastic parameters and anisotropic parameters
|

|
Slice of layers characterized by curvature (left) and curvature computed stress (right)
|

|
Slice of the layers with the maximum (right) and minimum stresses (left)
|

|
Comparison of horizontal slice of difference stress ratio under orthogonal anisotropy model (left) and calculation result of difference stress of well A logging curve (right)
|

|
Fault interpretation diagram of the target layer(The black line is the fault line)
|
| [1] |
黄荣樽, 陈勉, 邓金根 , 等. 泥页岩井壁稳定力学与化学的耦合研究[J]. 钻井液与完井液, 1995,12(3):15-21.
|
| [1] |
Huang R Z, Chen M, Deng J G , et al. Study on shale stability of wellbore by mechanics coupling with chemistry method[J]. Drilling Fluid and Completion Fluid, 1995,12(3):15-21.
|
| [2] |
葛洪魁, 王顺昌 . 地应力测试及其在勘探开发中的应用[J]. 中国石油大学学报:自然科学版, 1998,22(1):94-99.
|
| [2] |
Ge H K, Wang S C . Ground stress testing and its application in exploration and development[J]. Journal of China University of Petroleum, 1998,22(1):94-99.
|
| [3] |
景锋, 盛谦, 余美万 . 地应力与岩石弹性模量随埋深变化及相互影响[ C]//全国岩石力学与工程学术大会, 2010.
|
| [3] |
Jing F, Sheng Q, Yu M W . The change rule of geostress and the elatic modulus of rock with depth and their mutual impact[ C]//National Conference on Rock Mechanics and Engineering, 2010.
|
| [4] |
秦向辉, 孙进忠 . 地应力与岩石弹性模量关系试验研究[J]. 岩土力学, 2012,33(6):1689-1695.
|
| [4] |
Qin X H, Sun S Z . Experimental study of relation between in-situ crustal stress and rock elastic modulus.[J]. Rock and Soil Mechanics, 2012,33(6):1689-1695.
|
| [5] |
Gray F, Schmidt D, Delbecq F. Optimize shale gas field development using stresses and rock strength derived from 3D seismic data[C]// Canadian Uniconventional Resources and International Petroleum Conference, 2010.
|
| [6] |
Gray F D . Methods and systems for estimating stress using seismic data[P]. United States Patent Application,20110182144A1.
|
| [7] |
陈天胜, 魏修成, 刘洋 . 一种新的各向异性弹性阻抗近似公式[J]. 石油物探, 2006,45(6):563-569.
|
| [7] |
Chen T S, Wei X C, Liu Y . A new approximate formula for anisotropic elastic impedance[J]. Geophysical Prospecting for Petroleum, 2006,45(6):563-569.
|
| [8] |
Martins J L . An approach for elastic impedance in weakly anisotropic media[J]. SEG Technical Program Expanded Abstracts, 2002,21(1):2478.
|
| [9] |
马妮, 印兴耀, 孙成禹 , 等. 基于正交各向异性介质理论的地应力地震预测方法[J]. 地球物理学报, 2017,60(12):4766-4775.
|
| [9] |
Ma N, Yin X Y, Sun C Y , et al. The in-situ stress seismic prediction method based on the theory of orthorhombic anisotropic media[J]. Geophysics, 2017,60(12):4766-4775.
|
| [10] |
Rüger Andreas, Tsvankin I . Using AVO for fracture detection:Analytic basis and practical solutions[J]. The Leading Edge, 1997,16(10):1429-1434.
|
| [11] |
Hsu C J, Schoenberg M . Elastic waves through a simulated fractured medium[J]. Geophysics, 1993,58(7):964-977.
|
| [12] |
Fatti J L, Smith G C, Vail P J , et al. Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994,59(9):1362-1376.
|
| [13] |
李爱山, 印兴耀, 张繁昌 , 等. VTI介质中的弹性阻抗与参数提取[J]. 地球物理学进展, 2008,23(6):1878-1885.
|
| [13] |
Li A S, Yin X Y, Zhang F C , et al. Elastic impedance in vti media and parameter extraction[J]. Progress in Geophysics, 2008,23(6):1878-1885.
|
| [14] |
Connolly P . Elastic impedance[J]. Leading Edge, 1999,18(4):438-438.
|
| [15] |
Martins J L . Elastic impedance in weakly anisotropic media[J]. Geophysics, 2006,71(3):73.
|
| [16] |
Tarantola A. Inverse problem theory and methods for model parameter estimation[M]. Science Press, 2005.
|
| [17] |
Bakulin , Andrey , Grechka . et al. Estimation of fracture parameters from reflection seismic data-Part I:HTI model due to a single fracture set[J]. Geophysics, 2000,65(6):1788-1802.
|
| [18] |
Thomsen L, Anderson D L . Weak elastic anisotropy in global seismology[J]. 2014.
|
| [19] |
Hunt L, Reynolds S, Hadley S , et al. Causal fracture prediction Curvature,stress,and geomechanics[J]. Leading Edge, 2011,30(11):1274-1286.
|
|
|
|
