|
|
|
| Footprint analysis and footprint-FFT-based fast forward modeling of potential fields |
SUN Si-Yuan( ), GAO Xiu-He, CAO Xue-Feng ), GAO Xiu-He, CAO Xue-Feng |
| China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China |
|
|
|
|
Abstract Conventional inversion and forward modeling of large-scale potential field data from gravity and magnetic exploration, demanding high computer performance, exhibit low efficiency. Hence, this study defined a footprint determination method for potential fields, analyzed the influencing factors, and innovatively proposed a footprint-FFT strategy for forward modeling of potential fields. The footprint-FFT algorithm improved the forward modeling process from three aspects: (1) Kernel matrices were calculated based on the potential field-derived properties, significantly reducing their size; (2) A footprint concept for potential fields was introduced and defined, decoupling data scales from kernel matrix sizes, thus improving the kernel matrix computing efficiency and reducing the hardware cost; (3) Based on the above, the computing area was divided into subspaces, and the footprint-FFT strategy was first proposed for the batch computing of potential fields in subspaces, accelerating the forward modeling process. By reducing the computational complexity and storage of the kernel matrix, the method proposed in this study significantly improved the operational speed while ensuring computational accuracy. This method enabled the fast forward modeling of potential fields with more than 1 billion grids on a laptop computer within a few minutes. Theoretical examples demonstrate that this method has high efficiency and moderate requirements for computer configuration, manifesting considerable potential in the forward modeling and inversion of large-scale potential field data.
|
|
Received: 13 October 2023
Published: 26 February 2025
|
|
|
|
|
|
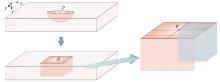
|
The equivalent diagram for footprint of potential field
|
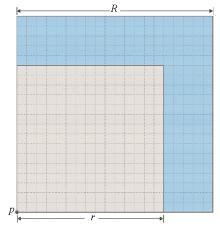
|
The relationship between radiuses of footprint and calculation
|
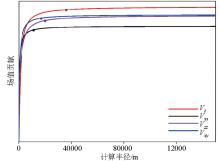
|
Curves of contributions for fields with calculation radius
(color dots represent radius of footprint for different fields)
|

|
Footprint radius of Vz and Vxx varies with (a) depth of region, (b) observation height, and (c) grid dimension
|

|
The Schematic of footprint-FFT method
|

|
The forward modeling results of rectangular anomalies
a—gravity field;b—magnetic field in perpendicular magnetization mode;c—magnetic field in incline magnetization mode
|

|
The absolute errors between our method and analytical solution
a—gravity field;b—magnetic field in perpendicular magnetization mode;c—in incline magnetization mode
|
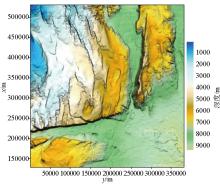
|
Depth variations of basement for Bishop complex model
|
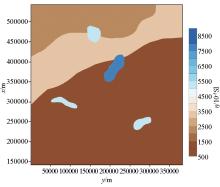
|
Variations of magnetic susceptibility for basement of Bishop model
|

|
The forward modeling results of Bishop model for (a) gravity field and (b) magnetic field
|
| [1] |
Li Y G, Oldenburg D W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method[J]. Geophysical Journal International, 2003, 152(2):251-265.
|
| [2] |
Davis K, Li Y G. Efficient 3D inversion of magnetic data via octree-mesh discretization,space-filling curves,and wavelets[J]. Geophysics, 2013, 78(5):J61-J73.
|
| [3] |
Martin R, Monteiller V, Komatitsch D, et al. Gravity inversion using wavelet-based compression on parallel hybrid CPU/GPU systems:Application to southwest Ghana[J]. Geophysical Journal International, 2013, 195(3):1594-1619.
|
| [4] |
Sun S Y, Yin C C, Gao X H, et al. Gravity compression forward modeling and multiscale inversion based on wavelet transform[J]. Applied Geophysics, 2018, 15(2):342-352.
|
| [5] |
Parker R L. The rapid calculation of potential anomalies[J]. Geophysical Journal International, 1973, 31(4):447-455.
|
| [6] |
Chai Y F, Hinze W J. Gravity inversion of an interface above which the density contrast varies exponentially with depth[J]. Geophysics, 1988, 53(6):837-845.
|
| [7] |
Caratori Tontini F, Cocchi L, Carmisciano C. Rapid 3D forward model of potential fields with application to the Palinuro Seamount magnetic anomaly (southern Tyrrhenian Sea,Italy)[J]. Journal of Geophysical Research:Solid Earth, 2009, 114(B2):B02103.
|
| [8] |
Sansò F, and M. G.Sideris, 2013, Geoid Determination: The forward modelling of the gravity field. Springer,Berlin,Heidelberg.
|
| [9] |
吴乐园. 重磁位场频率域高精度正演方法:Gauss-FFT法[D]. 杭州: 浙江大学, 2014.
|
| [9] |
Wu L Y. High-precision fourier-domain modeling of potential fields:Gauss-FFT method[D]. Hangzhou: Zhejiang University, 2014.
|
| [10] |
Wu L Y. Efficient modeling of gravity fields caused by sources with arbitrary geometry and arbitrary density distribution[J]. Surveys in Geophysics, 2018, 39(3):401-434.
|
| [11] |
Zhao G D, Chen B, Chen L W, et al. High-accuracy 3D Fourier forward modeling of gravity field based on the Gauss-FFT technique[J]. Journal of Applied Geophysics, 2018,150:294-303.
|
| [12] |
Jahandari H, Farquharson C G. Forward modeling of gravity data using finite-volume and finite-element methods on unstructured grids[J]. Geophysics, 2013, 78(3):G69-G80.
|
| [13] |
Farquharson C G, Mosher C R W. Three-dimensional modelling of gravity data using finite differences[J]. Journal of Applied Geophysics, 2009, 68(3):417-422.
|
| [14] |
Zhdanov M S. New advances in regularized inversion of gravity and electromagnetic data[J]. Geophysical Prospecting, 2009, 57(4):463-478.
|
| [15] |
Cuma M, Wilson G A, Zhdanov M S. Large-scale 3D inversion of potential field data[J]. Geophysical Prospecting, 2012,60(6):1186-1199.
|
| [16] |
Moorkamp M, Jegen M, Roberts A, et al. Massively parallel forward modeling of scalar and tensor gravimetry data[J]. Computers & Geosciences, 2010, 36(5):680-686.
|
| [17] |
陈召曦, 孟小红, 刘国峰, 等. 基于GPU的任意三维复杂形体重磁异常快速计算[J]. 物探与化探, 2012, 36(1):117-121.
|
| [17] |
Chen Z X, Meng X H, Liu G F, et al. The GPU-based parallel calculation of gravity and magnetic anomalies for 3D arbitrary bodies[J]. Geophysical and Geochemical Exploration, 2012, 36(1):117-121.
|
| [18] |
Chen Z X, Meng X H, Guo L H, et al. GICUDA:A parallel program for 3D correlation imaging of large scale gravity and gravity gradiometry data on graphics processing units with CUDA[J]. Computers & Geosciences, 2012,46:119-128.
|
| [19] |
Gross L, Altinay C, Shaw S. Inversion of potential field data using the finite element method on parallel computers[J]. Computers & Geosciences, 2015,84:61-71.
|
| [20] |
黄炎, 王庆宾, 冯进凯, 等. 局部地形改正快速计算的GPU并行的棱柱法[J]. 测绘学报, 2020, 49(11):1430-1437.
|
| [20] |
Huang Y, Wang Q B, Feng J K, et al. Rapid calculation of local topographic correction based on GPU parallel prism method[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(11):1430-1437.
|
| [21] |
Ascher U M, Haber E. Grid refinement and scaling for distributed parameter estimation problems[J]. Inverse Problems, 2001, 17(3):571-590.
|
| [22] |
May D A, Knepley M G. Optimal,scalable forward models for computing gravity anomalies[J]. Geophysical Journal International, 2011, 187(1):161-177.
|
| [23] |
Casenave F, Métivier L, Pajot-Métivier G, et al. Fast computation of general forward gravitation problems[J]. Journal of Geodesy, 2016, 90(7):655-675.
|
| [24] |
Ren Z Y, Tang J T, Kalscheuer T, et al. Fast 3D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method[J]. Journal of Geophysical Research:Solid Earth, 2017, 122(1):79-109.
|
| [25] |
Boulanger O, Chouteau M. Constraints in 3D gravity inversion[J]. Geophysical Prospecting, 2001, 49(2):265-280.
|
| [26] |
姚长利, 郝天珧, 管志宁, 等. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报, 2003, 46(2):252-258.
|
| [26] |
Yao C L, Hao T Y, Guan Z N, et al. High-speed computation and efficient storage in 3D gravity and magnetic inversion based on genetic algorithms[J]. Chinese Journal of Geophysics, 2003, 46(2):252-258.
|
| [27] |
Bruun C E, Nielsen T B. Algorithms and software for large-scale geophysical reconstructions[J]. Denmark:Technical University of Denmark, 2007.
|
| [28] |
Zhang Y L, Wong Y S. BTTB-based numerical schemes for three-dimensional gravity field inversion[J]. Geophysical Journal International, 2015, 203(1):243-256.
|
| [29] |
Chen L W, Liu L B. Fast and accurate forward modelling of gravity field using prismatic grids[J]. Geophysical Journal International, 2019, 216(2):1062-1071.
|
| [30] |
Hogue J D, Renaut R A, Vatankhah S. A tutorial and open source software for the efficient evaluation of gravity and magnetic kernels[J]. Computers & Geosciences, 2020,144:104575.
|
| [31] |
袁洋, 崔益安, 陈波, 等. 基于BTTB矩阵的快速高精度三维磁场正演[J]. 地球物理学报, 2022, 65(3):1107-1124.
|
| [31] |
Yuan Y, Cui Y A, Chen B, et al. Fast and high accuracy 3D magnetic anomaly forward modeling based on BTTB matrix[J]. Chinese Journal of Geophysics, 2022, 65(3):1107-1124.
|
| [32] |
Sun S Y, Gao X H, Cao X F. Fast 3D forward modeling of a potential field based on spherical symmetry of gravitational potential[J]. Geophysics, 2023, 88(3):G29-G42.
|
| [33] |
Cox L H, Zhdanov M S. Large-scale 3D inversion of HEM data using a moving footprint[C]// SEG Technical Program Expanded Abstracts 2007.Society of Exploration Geophysicists, 2007.
|
| [34] |
Cuma M, Zhdanov M S. Massively parallel regularized 3D inversion of potential fields on CPUs and GPUs[J]. Computers & Geosciences, 2014,62:80-87.
|
| [35] |
Liu Y H, Yin C C. 3D inversion for multipulse airborne transient electromagnetic data[J]. Geophysics, 2016, 81(6):E401-E408.
|
| [36] |
石泽玉, 张志厚, 刘鹏飞, 等. 重力及其梯度异常正演的Moving-footprint大尺度模型分解方法[J]. 物探与化探, 2022, 46(3):576-584.
|
| [36] |
Shi Z Y, Zhang Z H, Liu P F, et al. Moving-footprint-based large-scale model decomposition method for forward modeling of gravity and gravity gradient anomalies[J]. Geophysical and Geochemical Exploration, 2022, 46(3):576-584.
|
| [37] |
Williams S E, Fairhead J D, Flanagan G. Comparison of grid Euler deconvolution with and without 2D constraints using a realistic 3D magnetic basement model[J]. Geophysics, 2005, 70(3):L13-L21.
|
| [38] |
Barnes G, Lumley J. Processing gravity gradient data[J]. Geophysics, 2011, 76(2):I33-I47.
|
| [1] |
ZHANG Zi-Wei, LI Hou-Pu, ZHANG Heng-Lei, ZHU Dan. A low-rank decomposition-based method for separating gravity and magnetic anomalies and its application[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 118-128. |
| [2] |
JIANG Zhi-Qiang, LIN Chao, YANG Ting-Wei, NING Xiao-Bin. Forward modeling of a controllable-source 3D electromagnetic method based on fictitious wave field[J]. Geophysical and Geochemical Exploration, 2024, 48(5): 1348-1358. |
|
|
|
|

