|
|
|
| An improved butterfly optimization algorithm in the inversion of Rayleigh wave dispersion curve |
PENG Liu-Ya1( ), FENG Wei-Dong1, XIE Hui-Ting1, LI Fei1, YANG Yuan-Yuan1, CAO Jun-Feng1, REN Chuan2 ), FENG Wei-Dong1, XIE Hui-Ting1, LI Fei1, YANG Yuan-Yuan1, CAO Jun-Feng1, REN Chuan2 |
1. Anhui Earthquake Agency,Hefei 230031,China
2. Anhui Huizhou Geology Security Institute Co.,Ltd.,Hefei 231202,China |
|
|
|
|
Abstract Due to the multiplicity of solutions and the multiple extrema of the inversion objection functions,conventional nonlinear optimization algorithms are susceptible to unstable convergence and local optimum in the inversion of Rayleigh wave dispersion curves.This study improved the standard butterfly optimization algorithm by incorporating dynamic switch probability and nonlinear self-adaptive weight factors,yielding an elevated global exploration capacity in the early stage and a high local research ability in the latter stage.Furthermore,the dimension-by-dimension Cauchy mutation,along with a greedy algorithm,was employed to update the current best position during each iteration,ultimately directing the whole swarm population toward the global optimum.Tests of four commonly used benchmark functions demonstrate that the improved butterfly optimization algorithm(IBOA) outperformed other nonlinear algorithms,including the genetic algorithm and particle swarm optimization algorithm,in terms of the global research capacity of both unimodal and multimodal functions.Different algorithms were adopted for the inversion of the dispersion curves of three theoretical geological models.The results show that IBOA yielded inversion results that were closer to the models even when the dispersion curves contained 10% random noise.Finally,the IBOA was applied to actual Rayleigh wave data,and the inversion results were highly consistent with the strata revealed by drilling.Compared with the genetic algorithm and the particle swarm optimization algorithm,the IBOA significantly improved the convergence speed,as well as solution accuracy and stability.Therefore,the IBOA has a certain practical value and application prospects.
|
|
Received: 22 April 2023
Published: 27 June 2024
|
|
|
|
|
|
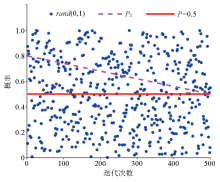
|
Dynamic switch probability
|
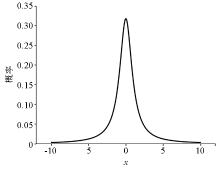
|
Probability density function of standard Cauchy distribution
|
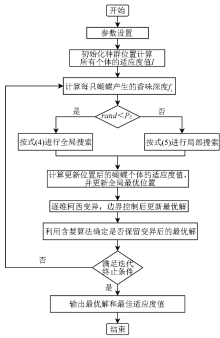
|
Flowchart of IBOA
|

| 函数名称 | 数学表达式 | 变量个数 | 搜索空间 | 最小值 | | Sphere | f(x)= | 30 | [-100,100] | 0 | | Schwefel 2.22 | f(x)= + | 30 | [-10,10] | 0 | | Griewank | f(x)=1+ - cos( ) | 30 | [-600,600] | 0 | | Rastrigin | f(x)= | 30 | [-5.12,5.12] | 0 |
|
Test functions
|
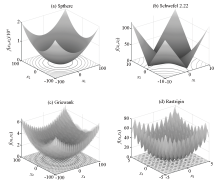
|
Plots of test functions with two dimensions
|

| 函数特点 | 函数名称 | 误差 | GA | PSO | BOA | IBOA | | 单峰函数 | Sphere | 平均值 | 0.1102 | 8.40×10-12 | 1.95×10-22 | 0 | | 标准差 | 0.0711 | 3.18×10-11 | 9.53×10-22 | 0 | | 最优值 | 0.0004 | 9.70×10-15 | 1.73×10-28 | 0 | | 最次值 | 0.2503 | 2.15×10-10 | 6.68×10-21 | 0 | | Schwefel 2.22 | 平均值 | 0.1465 | 0.0018 | 3.69×10-16 | 0 | | 标准差 | 0.0648 | 0.0070 | 5.10×10-16 | 0 | | 最优值 | 0.0030 | 9.75×10-8 | 9.70×10-19 | 0 | | 最次值 | 0.2894 | 0.0458 | 3.06×10-15 | 0 | | 多峰函数 | Griewank | 平均值 | 0.2633 | 0.0188 | 0 | 0 | | 标准差 | 0.1605 | 0.0238 | 0 | 0 | | 最优值 | 0.0040 | 3.74×10-14 | 0 | 0 | | 最次值 | 0.6071 | 0.1100 | 0 | 0 | | Rastrigin | 平均值 | 0.5285 | 10.6319 | 0 | 0 | | 标准差 | 0.6463 | 13.7308 | 0 | 0 | | 最优值 | 0.0001 | 1.14×10-13 | 0 | 0 | | 最次值 | 2.6254 | 29.8488 | 0 | 0 |
|
Optimization results of different algorithms
|
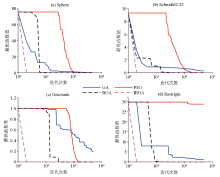
|
Convergence Characteristics of test functions by different algorithms
a—convergence curves of Sphere;b—convergence curves of Schwefel 2.22;c—convergence curves of Griewank;d—convergence curves of Rastrigin
|

| 函数名称 | GA | PSO | BOA | IBOA | | Sphere | 9.4 | 3.9 | 4.5 | 5.0 | | Schwefel 2.22 | 9.7 | 4.2 | 4.2 | 5.0 | | Griewank | 10.8 | 4.0 | 4.9 | 6.1 | | Rastrigin | 12.8 | 3.4 | 4.8 | 4.4 |
|
Consumed seconds of different algorithms under 50 trialss
|

| 地层序号 | 模型参数 | 搜索范围 | 横波速度Vs/
(m·s-1) | 厚度H/m | 横波速度Vs/
(m·s-1) | 厚度H/m | | 模型1(速度递增型地层) | | 1 | 150 | 2 | 75~225 | 1~3 | | 2 | 240 | 4 | 120~360 | 2~6 | | 3 | 360 | 6 | 180~540 | 3~9 | | 4 | 500 | 半空间 | 250~750 | 半空间 | | 模型2(含低速软夹层型地层) | | 1 | 200 | 2 | 60~300 | 1~3 | | 2 | 120 | 4 | 60~300 | 2~6 | | 3 | 300 | 6 | 150~450 | 3~9 | | 4 | 500 | 半空间 | 250~750 | 半空间 | | 模型3(含高速硬夹层型地层) | | 1 | 150 | 2 | 75~225 | 1~3 | | 2 | 300 | 4 | 100~500 | 2~6 | | 3 | 250 | 6 | 100~500 | 3~9 | | 4 | 500 | 半空间 | 250~750 | 半空间 |
|
Theoretical models and search range
|
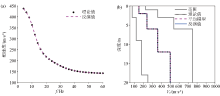
|
Inverted results of model 1 by IBOA without noise
a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model
|
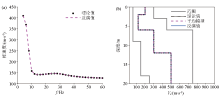
|
Inverted results of model 2 by IBOA without noise
a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model
|
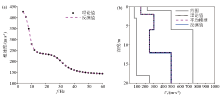
|
Inverted results of model 3 by IBOA without noise
a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model
|
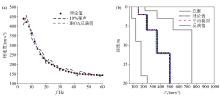
|
Inverted results of model 1 by IBOA with 10% random noise
a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model
|
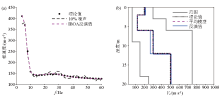
|
Inverted results of model 2 by IBOA with 10% random noise
a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model
|
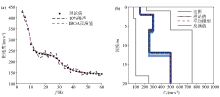
|
Inverted results of model 3 by IBOA with 10% random noise
a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model
|

| 模型编号 | 模型参数 | 理论值 | 无噪声 | 含10%随机噪声 | | 平均值 | 相对误差/% | 标准差 | 平均值 | 相对误差/% | 标准差 | | 模型1 | Vs1/(m·s-1) | 150 | 150.01 | 0.005 | 0.037 | 151.36 | 0.904 | 0.435 | | Vs2/(m·s-1) | 240 | 239.96 | 0.017 | 0.123 | 246.33 | 2.637 | 3.823 | | Vs3/(m·s-1) | 360 | 359.94 | 0.017 | 0.185 | 364.73 | 1.314 | 5.600 | | Vs4/(m·s-1) | 500 | 499.91 | 0.017 | 0.257 | 509.11 | 1.822 | 1.024 | | H1/m | 2 | 2.00 | 0.015 | 0.001 | 2.04 | 1.820 | 0.004 | | H2/m | 4 | 4.00 | 0.018 | 0.002 | 4.07 | 1.822 | 0.008 | | H3/m | 6 | 6.00 | 0.017 | 0.003 | 6.11 | 1.822 | 0.012 | | 模型2 | Vs1/(m·s-1) | 200 | 200.00 | 0.002 | 0.359 | 206.59 | 3.293 | 4.064 | | Vs2/(m·s-1) | 120 | 120.00 | 0.001 | 0.086 | 119.61 | 0.324 | 1.246 | | Vs3/(m·s-1) | 300 | 300.00 | 0.001 | 0.215 | 299.56 | 0.147 | 11.391 | | Vs4/(m·s-1) | 500 | 500.00 | 0.001 | 0.358 | 505.19 | 1.038 | 1.582 | | H1/m | 2 | 2.00 | 0.000 | 0.001 | 2.02 | 1.040 | 0.006 | | H2/m | 4 | 4.00 | 0.000 | 0.003 | 4.04 | 1.038 | 0.013 | | H3/m | 6 | 6.00 | 0.000 | 0.004 | 6.06 | 1.038 | 0.019 | | 模型3 | Vs1/(m·s-1) | 150 | 149.99 | 0.005 | 0.599 | 150.38 | 0.252 | 5.109 | | Vs2/(m·s-1) | 300 | 300.98 | 0.326 | 1.709 | 302.61 | 0.871 | 7.384 | | Vs3/(m·s-1) | 250 | 249.83 | 0.067 | 0.866 | 257.15 | 2.860 | 6.338 | | Vs4/(m·s-1) | 500 | 500.38 | 0.075 | 2.591 | 502.89 | 0.578 | 5.939 | | H1/m | 2 | 2.00 | 0.081 | 0.012 | 2.03 | 1.515 | 0.130 | | H2/m | 4 | 4.00 | 0.104 | 0.032 | 4.20 | 4.880 | 0.234 | | H3/m | 6 | 6.01 | 0.092 | 0.054 | 5.95 | 0.896 | 0.172 |
|
Statistics of inverted results for theoretical models
|
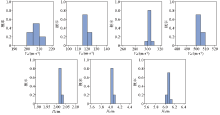
|
Histogram of inverted results of model 2 by IBOA with 10% random noise
|
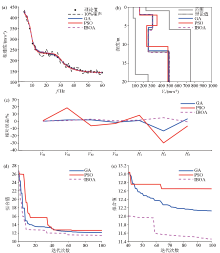
|
Inverted results of model 3 by different algorithms with 10% random noise
a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model;c—relative error between theoretical model and inverted model;d—convergence curves of different algorithms;e—convergence curves of different algorithms during iteration No.40~100
|
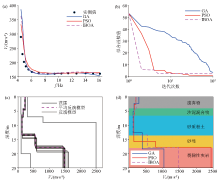
|
Inverted results of actual field data by different algorithms
a—dispersion curves of measured data and inverted models by different algorithms;b—convergence curves of different algorithms;c—shear wave structures of 10 times inversions by IBOA;d—comparison between actual borehole data and inverted models
|

| 层序号 | 横波速度Vs/
(m·s-1) | 厚度H/m | 密度ρ/
(g·cm-3) | 泊松比 | | 1 | 90~300 | 2~6 | 1.9 | 0.45 | | 2 | 100~300 | 1~4 | 1.9 | 0.45 | | 3 | 100~300 | 4~10 | 2.0 | 0.45 | | 4 | 400~800 | 2~6 | 2.2 | 0.25 | | 5 | 1000~2500 | - | 2.4 | 0.20 |
|
Search range for inversion parameters at each layer
|
| [1] |
李庆春, 邵广周, 刘金兰, 等. 瑞雷面波勘探的过去、现在和未来[J]. 地球科学与环境学报, 2006, 28(3):74-77.
|
| [1] |
Li Q C, Shao G Z, Liu J L, et al. Past,present and future of Rayleigh surface wave exploration[J]. Journal of Earth Sciences and Environment, 2006, 28(3):74-77.
|
| [2] |
夏江海, 高玲利, 潘雨迪, 等. 高频面波方法的若干新进展[J]. 地球物理学报, 2015, 58(8):2591-2605.
|
| [2] |
Xia J H, Gao L L, Pan Y D, et al. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 2015, 58(8):2591-2605.
|
| [3] |
Pan Y D, Gao L L, Bohlen T. High-resolution characterization of near-surface structures by surface-wave inversions:From dispersion curve to full waveform[J]. Surveys in Geophysics, 2019, 40(2):167-195.
|
| [4] |
宋先海, 张学强, 王一鸣, 等. 近地表弹性介质瑞雷波勘探研究进展与展望[J]. 地质科技通报, 2020, 39(5):173-182.
|
| [4] |
Song X H, Zhang X Q, Wang Y M, et al. Recent advances and prospects of near surface elastic Rayleigh waves[J]. Bulletin of Geological Science and Technology, 2020, 39(5):173-182.
|
| [5] |
Xia J H, Miller R D, Park C B, et al. Comparing shear-wave velocity profiles inverted from multichannel surface wave with borehole measurements[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(3):181-190.
|
| [6] |
Xia J H. Estimation of near-surface shear-wave velocities and quality factors using multichannel analysis of surface-wave methods[J]. Journal of Applied Geophysics, 2014,103:140-151.
|
| [7] |
向晓松, 贾继标, 李士祥. 面波勘探在地基液化判别中的应用与探讨[J]. 矿产勘查, 2011, 2(1):97-101.
|
| [7] |
Xiang X S, Jia J B, Li S X. Application and study of surface wave exploration in distinguishing foundation liquefaction[J]. Mineral Exploration, 2011, 2(1):97-101.
|
| [8] |
李启成, 闫晓丹, 孙颖川, 等. 利用瑞利面波进行岩性分层[J]. 地球物理学进展, 2016, 31(5):2124-2127.
|
| [8] |
Li Q C, Yan X D, Sun Y C, et al. Measurement of superstratum wave velocity with reflection wave on dip section[J]. Progress in Geophysics, 2016, 31(5):2124-2127.
|
| [9] |
赵东, 王光杰, 王兴泰, 等. 用遗传算法进行瑞利波反演[J]. 物探与化探, 1995, 19(3):178-185.
|
| [9] |
Zhao D, Wang G J, Wang X T, et al. The application of genetic algorithm to Rayleigh wave inversion[J]. Geophysical and Geochemical Exploration, 1995, 19(3):178-185.
|
| [10] |
Yamanaka H, Ishida H. Application of genetic algorithms to an inversion of surface-wave dispersion data[J]. Bulletin of the Seismological Society of America, 1996, 86(2):436-444.
|
| [11] |
Song X H, Tang L, Lyu X C, et al. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves[J]. Journal of Applied Geophysics, 2012,84:1-13.
|
| [12] |
张晓阳, 杜文凤, 卢勇旭. 粒子群算法在面波频散曲线反演中的应用[J]. 辽宁工程技术大学学报:自然科学版, 2016, 35(12):1527-1532.
|
| [12] |
Zhang X Y, Du W F, Lu Y X. The application of particle swarm optimization in the inversion of Rayleigh wave dispersion curve[J]. Journal of Liaoning Technical University:Natural Science Edition, 2016, 35(12):1527-1532.
|
| [13] |
蔡伟, 宋先海, 袁士川, 等. 利用粒子群优化算法快速、稳定反演瑞雷波频散曲线[J]. 石油地球物理勘探, 2018, 53(1):25-34.
|
| [13] |
Cai W, Song X H, Yuan S C, et al. Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization[J]. Oil Geophysical Prospecting, 2018, 53(1):25-34.
|
| [14] |
彭刘亚, 任川. 基于粒子群算法的瑞雷波频散曲线反演研究[J]. 地球物理学进展, 2018, 33(4):1682-1686.
|
| [14] |
Peng L Y, Ren C. Inversion of Rayleigh wave dispersion curve using particle swarm optimization algorithm[J]. Progress in Geophysics, 2018, 33(4):1682-1686.
|
| [15] |
彭刘亚, 任川, 冯伟栋. 多模式瑞雷波频散曲线的粒子群反演方法研究[J]. 地球物理学进展, 2018, 33(3):1262-1268.
|
| [15] |
Peng L Y, Ren C, Feng W D. Multimodal Rayleigh wave dispersion curve inversion by particle swarm optimization[J]. Progress in Geophysics, 2018, 33(3):1262-1268.
|
| [16] |
侯征, 熊盛青, 杨进, 等. 基于人工蜂群算法的瑞雷波多阶模式非线性联合反演研究[J]. 地球物理学进展, 2018, 33(1):362-371.
|
| [16] |
Hou Z, Xiong S Q, Yang J, et al. Research on nonlinear joint inversion of multimode Rayleigh wave based on artificial bee colony algorithm[J]. Progress in Geophysics, 2018, 33(1):362-371.
|
| [17] |
于东凯, 宋先海, 江东威, 等. 改进蜂群算法及其在面波频散曲线反演中的应用[J]. 地球物理学报, 2018, 61(4):1482-1495.
|
| [17] |
Yu D K, Song X H, Jiang D W, et al. Improvement of Artificial Bee Colony and its application in Rayleigh wave inversion[J]. Chinese Journal of Geophysics, 2018, 61(4):1482-1495.
|
| [18] |
于东凯, 宋先海, 张学强, 等. 蚱蜢算法在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2019, 54(2):288-301.
|
| [18] |
Yu D K, Song X H, Zhang X Q, et al. Rayleigh wave dispersion inversion based on grasshopper optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(2):288-301.
|
| [19] |
高旭, 于静, 李学良, 等. 自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2021, 56(4):745-757.
|
| [19] |
Gao X, Yu J, Li X L, et al. Rayleigh wave dispersion curve inversion based on adaptive weight dragonfly algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4):745-757.
|
| [20] |
崔建文. 一种改进的全局优化算法及其在面波频散曲线反演中的应用[J]. 地球物理学报, 2004, 47(3):521-527.
|
| [20] |
Cui J W. An improved global optimization method and its application to the inversion of surface wave dispersion curves[J]. Chinese Journal of Geophysics, 2004, 47(3):521-527.
|
| [21] |
杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6):1217-1227.
|
| [21] |
Yang B, Xiong Z Q, Zhang D Z, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4):2019, 54(6):1217-1227.
|
| [22] |
蔡伟, 宋先海, 袁士川, 等. 基于萤火虫和蝙蝠群智能算法的瑞雷波频散曲线反演[J]. 地球物理学报, 2018, 61(6):2409-2420.
|
| [22] |
Cai W, Song X H, Yuan S C, et al. Inversion of Rayleigh wave dispersion curves based on firefly and bat algorithms[J]. Chinese Journal of Geophysics, 2018, 61(6):2409-2420.
|
| [23] |
王一鸣, 宋先海, 张学强. 瑞雷面波频散曲线的粒子群蚁群混合优化反演[J]. 石油地球物理勘探, 2022, 57(2):303-310.
|
| [23] |
Wang Y M, Song X H, Zhang X Q. Inversion of Rayleigh wave dispersion curves based on particle swarm and ant colony hybrid optimization[J]. Oil Geophysical Prospecting, 2022, 57(2):303-310.
|
| [24] |
李翠琳, Stan E Dosso, Hefeng Dong. 根据非线性贝叶斯理论的界面波频散曲线反演[J]. 声学学报, 2012, 37(3):225-231.
|
| [24] |
Li C L, Dosso S, Dong H F. Interface-wave dispersion curves inversion based on nonlinear Bayesian theory[J]. Acta Acustica, 2012, 37(3):225-231.
|
| [25] |
付代光, 刘江平, 周黎明, 等. 基于贝叶斯理论的软夹层多模式瑞雷波频散曲线反演研究[J]. 岩土工程学报, 2015, 37(2):321-329.
|
| [25] |
Fu D G, Liu J P, Zhou L M, et al. Inversion of multimode Rayleigh-wave dispersion curves of soft interlayer based on Bayesian theory[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2):321-329.
|
| [26] |
付代光, 肖国强, 周黎明, 等. 基于非线性贝叶斯理论和BIC准则的防渗墙高精度瑞雷波反演研究[J]. 水利水电技术, 2018, 49(8):64-70.
|
| [26] |
Fu D G, Xiao G Q, Zhou L M, et al. Nonlinear Bayesian theory and BIC criterion-based study on high precision Rayleigh wave inversion of cutoff-wall[J]. Water Resources and Hydropower Engineering, 2018, 49(8):64-70.
|
| [27] |
刘辉, 李静, 曾昭发, 等. 基于贝叶斯理论面波频散曲线随机反演[J]. 物探与化探, 2021, 45(4):951-960.
|
| [27] |
Liu H, Li J, Zeng Z F, et al. Stochastic inversion of surface wave dispersion curves based on Bayesian theory[J]. Geophysical and Geochemical Exploration, 2021, 45(4):951-960.
|
| [28] |
刘昊楠, 张致付, 陈凯. 瑞利面波频散曲线贝叶斯反演及其在活断层调查中的应用[J]. 地球物理学进展, 2020, 35(4):1584-1589.
|
| [28] |
Liu H N, Zhang Z F, Chen K. Bayesian inversion of Rayleigh surface wave dispersion and its application in active fault investigation[J]. Progress in Geophysics, 2020, 35(4):1584-1589.
|
| [29] |
贺懿, 张进, 刘怀山. 基于神经网络的面波迭代反演应用研究[J]. 西南石油大学学报:自然科学版, 2010, 32(1):40-44.
|
| [29] |
He Y, Zhang J, Liu H S. Study on the application of iterative inversion of surface wave based on artificial neural network[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32(1):40-44.
|
| [30] |
魏继祖, 丁彦礼, 单娜琳, 等. 多阶模态瑞利面波频散曲线的BP神经网络反演[J]. 工程地球物理学报, 2012, 9(6):646-653.
|
| [30] |
Wei J Z, Ding Y L, Shan N L, et al. Study on BP inversion of the multi-modes Rayleigh wave[J]. Chinese Journal of Engineering Geophysics, 2012, 9(6):646-653.
|
| [31] |
曹旭, 熊章强, 张大洲. 基于BP神经网络的瑞雷面波智能优化反演[J]. 工程地球物理学报, 2015, 12(4):514-519.
|
| [31] |
Cao X, Xiong Z Q, Zhang D Z. The Rayleigh surface wave intelligent inversion based on the BP artificial neural network[J]. Chinese Journal of Engineering Geophysics, 2015, 12(4):514-519.
|
| [32] |
王一鸣, 宋先海, 张学强. 应用人工神经网络算法的地震面波非线性反演[J]. 石油地球物理勘探, 2021, 56(5):979-991.
|
| [32] |
Wang Y M, Song X H, Zhang X Q. Research on nonlinear inversion of seismic surface waves based on artificial neural network algorithm[J]. Oil Geophysical Prospecting, 2021, 56(5):979-991.
|
| [33] |
张志厚, 石泽玉, 马宁, 等. 瑞雷波频散曲线的深度学习反演方法[J]. 地球物理学报, 2022, 65(6):2244-2259.
|
| [33] |
Zhang Z H, Shi Z Y, Ma N, et al. Deep learning inversion of Rayleigh dispersion curves[J]. Chinese Journal of Geophysics, 2022, 65(6):2244-2259.
|
| [34] |
Arora S, Singh S. Butterfly algorithm with Levy flights for global optimization[C]// Waknaghat: 2015 International Conference on Signal Processing,Computing and Control(ISPCC).IEEE,2015: 220-224.
|
| [35] |
Arora S, Singh S. An improved butterfly optimization algorithm with chaos[J]. Journal of Intelligent & Fuzzy Systems, 2017, 32(1):1079-1088.
|
| [36] |
Arora S, Singh S. Butterfly optimization algorithm:A novel approach for global optimization[J]. Soft Computing, 2019, 23(3):715-734.
|
| [37] |
Raguso R A. Wake up and smell the roses:The ecology and evolution of floral scent[J]. Annual Review of Ecology,Evolution,and Systematics, 2008,39:549-569.
|
| [38] |
宁杰琼, 何庆. 混合策略改进的蝴蝶优化算法[J]. 计算机应用研究, 2021, 38(6):1718-1723,1738.
|
| [38] |
Ning J Q, He Q. Mixed strategy to improve butterfly optimization algorithm[J]. Application Research of Computers, 2021, 38(6):1718-1723,1738.
|
| [39] |
刘凯, 代永强. 融合变异策略的自适应蝴蝶优化算法[J]. 计算机应用研究, 2022, 39(1):134-140,145.
|
| [39] |
Liu K, Dai Y Q. Adaptive butterfly optimization algorithm based on mutation strategies[J]. Application Research of Computers, 2022, 39(1):134-140,1455.
|
| [40] |
郑洪清, 冯文健, 周永权. 融合正弦余弦算法的蝴蝶优化算法[J]. 广西科学, 2021, 28(2):152-159.
|
| [40] |
Zheng H Q, Feng W J, Zhou Y Q. Butterfly optimization algorithm based on sine cosine algorithm[J]. Guangxi Sciences, 2021, 28(2):152-159.
|
| [41] |
高文欣, 刘升, 肖子雅, 等. 柯西变异和自适应权重优化的蝴蝶算法[J]. 计算机工程与应用, 2020, 56(15):43-50.
|
| [41] |
Gao W X, Liu S, Xiao Z Y, et al. Butterfly optimization algorithm based on cauchy variation and adaptive weight[J]. Computer Engineering and Applications, 2020, 56(15):43-50.
|
| [42] |
凡友华, 刘家琦. 层状介质中瑞雷面波的频散研究[J]. 哈尔滨工业大学学报, 2001, 33(5):577-581.
|
| [42] |
Fan Y H, Liu J Q. Research on the dispersion of rayleigh waves in multilayered media[J]. Journal of Harbin Institute of Technology, 2001, 33(5):577-581.
|
| [43] |
董智开, 段文胜, 肖承文, 等. 基于快速标量传递算法的瑞雷波频散曲线反演研究[J]. 北京大学学报:自然科学版, 2020, 56(4):614-628.
|
| [43] |
Dong Z K, Duan W S, Xiao C W, et al. Inversion research of Rayleigh wave dispersion curve based on fast scalar transfer algorithm[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2020, 56(4):614-628.
|
| [44] |
Dal Moro G, Pipan M, Gabrielli P. Rayleigh wave dispersion curve inversion via genetic algorithms and Marginal Posterior Probability density estimation[J]. Journal of Applied Geophysics, 2007, 61(1):39-55.
|
| [45] |
王天琦, 于东凯, 蔡润. 基于改进蚁群算法在面波频散曲线反演中的应用[J]. 地震工程学报, 2020, 42(6):1523-1533.
|
| [45] |
Wang T Q, Yu D K, Cai R. Application of the improved ant colony algorithm in the inversion of Rayleigh wave dispersion curves[J]. China Earthquake Engineering Journal, 2020, 42(6):1523-1533.
|
| [1] |
YAO Yu, ZHANG Zhi-Hou. Intelligent inversion of magnetotelluric data based on improved DenseNet[J]. Geophysical and Geochemical Exploration, 2024, 48(3): 759-767. |
| [2] |
WANG Zhen, JI Zhi-Feng, ZHANG Yi-Qiong, WANG Xue-Ke, JIANG Li, LIN Ya-Ping, KONG Ling-Hong, ZHANG Ming-Jun. Research and application of the velocity modeling method for the eastern margin of the Pre-Caspian Basin[J]. Geophysical and Geochemical Exploration, 2024, 48(3): 794-803. |
|
|
|
|

