|
|
|
| Forward modeling of the seismic wave field of pure qP waves in TTI media based on the pseudo-analytical method |
ZHANG Kui-Tao1( ), LIAO Jia-Rong1, GU Han-Ming2( ), LIAO Jia-Rong1, GU Han-Ming2( ), SUN Ying-Ying1, CHEN Yi-Yang1, WANG Kai1 ), SUN Ying-Ying1, CHEN Yi-Yang1, WANG Kai1 |
1. Jiangxi Provincial Transportation Design and Research Institute Co.,Ltd.,Nanchang 330052,China
2. School of Geophysics and Geomatics,China University of Geosciences(Wuhan),Wuhan 430074,China |
|
|
|
|
Abstract Forward modeling and reverse-time migration imaging techniques for pure quasi-P (qP) waves in anisotropic media have aroused extensive concern in recent years.However,conventional quasi-acoustic equations are subjected to the interference from quasi-shear waves,the limitation of model parameters (ε≥δ),propagation instability,and low calculation accuracy,thus significantly restricting their application.Hence,this study shifted the quasi-differential equation of qP waves to the space-wavenumber domain and derived the second-order pure qP wave equation of TTI media in the time domain through coordinate transformation.To improve the calculation accuracy,this study conducted the forward modeling of the seismic wave field of pure qP waves in TTI media based on the pseudo-analytical method (PAM).The numerical simulation results show that:(1)The method proposed in this study was free from the limitations of quasi-acoustic equations,the interference from quasi-shear waves,and model parameters,enabling stable propagation of the seismic wave field;(2)Compared to other methods,the PAM can effectively improve the numerical simulation accuracy;(3)The testing of simple and complex models verified the correctness and applicability of the proposed method.
|
|
Received: 06 March 2023
Published: 26 February 2024
|
|
|
|
|
|
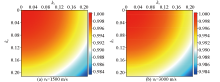
|
Normalized pseudo-Laplace(NPL) operator
|
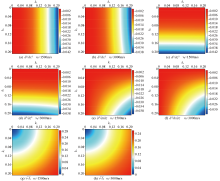
|
A second derivative of space based on normalized pseudo-Laplace(NPL) operators
|
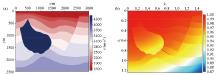
|
Normalized pseudo-Laplace (NPL) operator under complex media model
a—Hess complex media model;b—NPL for the Hess model
|

| 介质类型 | v0/(m·s-1) | ρ/(g·cm-3) | ε | δ | θ | | Ⅰ | 1700 | 2.5 | 0.20 | 0.10 | 0° | | Ⅱ | 1700 | 2.5 | 0.20 | 0.10 | 90° | | Ⅲ | 1700 | 2.5 | 0.20 | 0.10 | 45° | | Ⅳ | 1700 | 2.5 | 0.15 | 0.15 | 45° | | Ⅴ | 1700 | 2.5 | 0.10 | 0.20 | 45° |
|
Homogeneous media model parameters
|

|
Snapshot of the 400 ms moment wave field for uniform acoustic TTI medium pseudoacoustic wave equation (top) and pure qP wave equation (bottom)
a,d—corresponding media type III;b,e—corresponding media type IV;c,f—corresponding media type V
|

|
Pure qP wave equation snapshot of the wave field at 400 ms in a homogeneous anisotropic medium
a—media type Ⅰ; b—media type Ⅱ; c—media type Ⅲ
|

|
Snapshot of the 350 ms time wave of pure qP wave in uniform TTI medium
a—finite difference method(FDM); b—pseudo spectral method(PSM); c—pseudo analytical method(PAM)
|
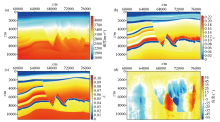
|
Two-dimensional BP2007 acoustic TTI media model parameters
a—P-wave velocity v0;b—P-wave anisotropy parameters ε;c—variation coefficient δ;d—polarization angle θ
|

|
Two-dimensional BP2007 acoustic TTI medium 4 s time wave field snapshot(a) and seismic record(b)
|
| [1] |
Chichinina T, Obolentseva I, Gik L, et al. Attenuation anisotropy in the linear-slip model: Interpretation of physical modeling data[J]. Geophysics, 2009, 74(5):WB165-WB176.

|
| [2] |
丁亮, 刘洋. 逆时偏移成像技术研究进展[J]. 地球物理学进展, 2011, 26(3):1085-1100.
|
| [2] |
Ding L, Liu Y. Progress in reverse time migration imaging[J]. Progress in Geophysics, 2011, 26(3):1085-1100.
|
| [3] |
Alkhalifah T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4):1239-1250.

|
| [4] |
Alkhalifah T. Acoustic approximations for processing in transversely isotropic media[J]. Geophysics, 1998, 63(2):623-631.

|
| [5] |
Du X, Bancroft J C, Lines L R. Reverse-time migration for tilted TI media[C]// SEG Technical Program Expanded Abstracts 2005,Society of Exploration Geophysicists, 2005:1930-1933.
|
| [6] |
Zhou H B, Zhang G Q, Bloor R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[C]// SEG Technical Program Expanded Abstracts 2006,Society of Exploration Geophysicists, 2006:194-198.
|
| [7] |
Duveneck E, Milcik P, Bakker P M, et al. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[C]// SEG Technical Program Expanded Abstracts 2008,Society of Exploration Geophysicists, 2008:2186-2190.
|
| [8] |
程玖兵, 陈茂根, 王腾飞, 等. 各向异性介质qP波传播描述Ⅱ:分离纯模式标量波[J]. 地球物理学报, 2014, 57(10):3389-3401.
|
| [8] |
Cheng J B, Chen M G, Wang T F, et al. Description of qP-wave propagation in anisotropic media,Part II:Separation of pure-mode scalar waves[J]. Chinese Journal of Geophysics, 2014, 57(10):3389-3401.
|
| [9] |
程玖兵, 康玮, 王腾飞. 各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程[J]. 地球物理学报, 2013, 56(10):3474-3486.
|
| [9] |
Cheng J B, Kang W, Wang T F. Description of qP-wave propagation in anisotropic media,Part Ⅰ:Pseudo-pure-mode wave equations[J]. Chinese Journal of Geophysics, 2013, 56(10):3474-3486.
|
| [10] |
Duveneck E, Bakker P M. Stable P-wave modeling for reverse-time migration in tilted TI media[J]. Geophysics, 2011, 76(2):S65-S75.

|
| [11] |
Grechka V, Zhang L B, Rector J W III. Shear waves in acoustic anisotropic media[J]. Geophysics, 2004, 69(2):576-582.

|
| [12] |
郭成锋, 杜启振, 张明强, 等. 改进的TTI介质纯P波方程正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(1):258-270.
|
| [12] |
Guo C F, Du Q Z, Zhang M Q, et al. Numerical simulation and reverse time migration using an improved pure P-wave equation in tilted transversely isotropic media[J]. Chinese Journal of Geophysics, 2017, 60(1):258-270.
|
| [13] |
Zhang Y, Zhang H Z, Zhang G Q. A stable TTI reverse time migration and its implementation[J]. Geophysics, 2011, 76(3):WA3-WA11.

|
| [14] |
Zhan G, Pestana R C, Stoffa P L. Decoupled equations for reverse time migration in tilted transversely isotropic media[J]. Geophysics, 2012, 77(2):T37-T45.

|
| [15] |
Xu S, Tang B, Mu J, et al. Quasi-P wave propagation with an elliptic differential operator[C]// New Orleans: SEG Technical Program Expanded Abstracts 2015,Society of Exploration Geophysicists, 2015:4380-4384.
|
| [16] |
胡书华, 王宇超, 刘文卿, 等. 复杂TTI介质稳定的纯qP波波场模拟方法[J]. 石油地球物理勘探, 2018, 53(2):280-287,221.
|
| [16] |
Hu S H, Wang Y C, Liu W Q, et al. Pure quasi-P wave stable simulation in complex TTI media[J]. Oil Geophysical Prospecting, 2018, 53(2):280-287,221.
|
| [17] |
张庆朝, 朱国维, 周俊杰, 等. TTI介质qP波伪谱法正演模拟[J]. 石油地球物理勘探, 2019, 54(2):302-311,236.
|
| [17] |
Zhang Q C, Zhu G W, Zhou J J, et al. qP-wave numerical simulation in TTI media with pseudo-spectral method[J]. Oil Geophysical Prospecting, 2019, 54(2):302-311,236.
|
| [18] |
顾汉明, 张奎涛, 刘春成, 等. 基于Low-rank一步法波场延拓的黏声各向异性介质纯qP波正演模拟[J]. 石油地球物理勘探, 2020, 55(4):733-746,699-700.
|
| [18] |
Gu H M, Zhang K T, Liu C C, et al. Low-rank one-step wave extrapolation for pure qP-wave forward modeling in viscoacoustic anisotropic media[J]. Oil Geophysical Prospecting, 2020, 55(4):733-746,699-700.
|
| [19] |
Kreiss H O, Oliger J. Comparison of accurate methods for the integration of hyperbolic equations[J]. Tellus, 1972, 24(3):199-215.
|
| [20] |
Etgen J T, Brandsberg-Dahl S. The pseudo-analytical method:Application of pseudo-Laplacians to acoustic and acoustic anisotropic wave propagation[C]// SEG Technical Program Expanded Abstracts 2009,Society of Exploration Geophysicists, 2009:2552-2556.
|
| [21] |
Chu C L, Stoffa P L. Acoustic anisotropic wave modeling using normalized pseudo-laplacian[C]// SEG Technical Program Expanded Abstracts 2010,Society of Exploration Geophysicists, 2010:2972-2976.
|
| [22] |
张衡, 刘洪, 丁仁伟, 等. TTI介质伪解析解耦波动方程[J]. 地球物理学进展, 2016, 31(4):1752-1761.
|
| [22] |
Zhang H, Liu H, Ding R W, et al. Pseudo-analytical decoupled wave equation for TTI media[J]. Progress in Geophysics, 2016, 31(4):1752-1761.
|
| [23] |
Xu S, Zhou H B. Accurate simulations of pure quasi-P-waves in complex anisotropic media[J]. Geophysics, 2014, 79(6):T341-T348.

|
| [24] |
Xu W C, Li Z C, Deng W Z, et al. Anisotropic viscoacoustic wave RTM based on second-order quasi-differential equation[C]// New Orleans: SEG Technical Program Expanded Abstracts 2015,Society of Exploration Geophysicists, 2015:4013-4017.
|
|
|
|

