|
|
|
| 3D correlation tomography inversion of gravity anomalies constrained by edge features and depth weighting |
AN Guo-Qiang1( ), LU Bao-Liang1,2,3( ), LU Bao-Liang1,2,3( ), GAO Xin-Yu1, ZHU Wu1,3,4, LI Bo-Sen1 ), GAO Xin-Yu1, ZHU Wu1,3,4, LI Bo-Sen1 |
1. School of Geological Engineering and Geomatics, Chang’an University, Xi'an 710054, China
2. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China
3. Key Laboratory of Western Mineral Resources and Geological Engineering, Ministry of Education, Chang'an University, Xi'an 710054, China
4. Key Laboratory of Ecological Geology and Disaster Prevention, Ministry of Natural Resources, Xi'an 710054, China |
|
|
|
|
Abstract Correlation tomography is a fast tomography method using correlation coefficients to qualitatively interpret the spatial positions of geobodies. This method, featuring simple, stable, and fast calculations, can quickly and efficiently obtain the distribution of subsurface anomalies without solving large equations. However, the results of direct correlation tomography of gravity anomalies display deep divergence, excessive depth weighting function parameters, and low lateral and vertical resolution between anomalies. According to the fundamental principle of 3D correlation tomography inversion of gravity anomalies, this study introduced the balanced vertical derivative and balanced analytic signal amplitude of gravity anomalies as the edge features to horizontally weight the gravity anomaly correlation tomography, and proposed a more concise depth weighting function. As demonstrated by model tests, the lateral resolution of correlation tomography was improved under the constraint of gravity anomaly edge features, and the vertical resolution of correlation tomography was enhanced using the new depth weighting function. Finally, the method in this study was applied to the actual data of the Australian Olympic Dam polymetallic deposit, yielding consistent weighted tomography results with the actual geological data, thus proving the correctness and effectiveness of the method.
|
|
Received: 15 February 2023
Published: 26 February 2024
|
|
|
|
|
|
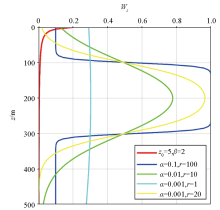
|
The depth weighting function proposed by predecessors
(z1=100m,z2=300m,zmax=500m)
|
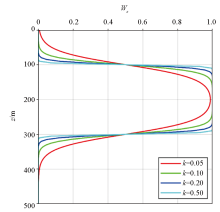
|
The depth weighting function proposed in this article
(z1=100m,z2=300m)
|
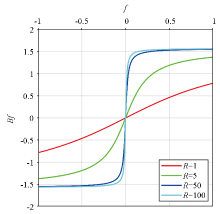
|
Arctangent balance functions with different balance coefficients
|

| 编号 | 模型名称 | x方向位置/m | y方向位置/m | z方向位置/m | 剩余密度/
(g·c ) | | | 1 | 直立长方体 | [250,450] | [400,600] | [100,300] | 1.0 | 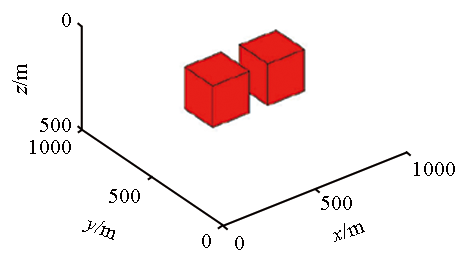 | | 2 | 直立长方体 | [550,750] | [400,600] | [100,300] | 1.0 |
|
Model parameters (including 5% noise)
|

|
Forward results of two anomalous bodies (including 5% noise) with a residual density of 1.0 g/cm3 and a distance of 100 m
a—gravity anomaly;b—normalize the balanced vertical derivative (nBVDR);c—Normalize the balanced analytical signal amplitude (nBASM)
|
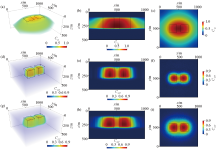
|
Weighted results of Correlation tomography of two anomalous bodies (including 5% noise) with a residual density of 1.0 g/cm3 and a distance of 100 m
a—imaging results with depth weighted constraints;b—vertical slice at y=500 m(depth weighted constraints);c—horizontal slice at z=200m(depth weighted constraints);d—imaging results of the method in this article (Wz+VDR weighted);e—vertical slice at y=500 m(Wz+VDR weighted);f—Horizontal slice at z=200 m(Wz+VDR weighted);g—imaging results of the method in this article (Wz+ASM weighted);h—vertical slice at y=500 m(Wz+ASM weighted);i—horizontal slice at z=200 m(Wz+ASM weighted)
|

| 编号 | 模型名称 | x方向位置/m | y方向位置/m | z方向位置/m | 剩余密度/
(g·c ) | | | 1 | 直立长方体 | [400,800] | [800,900] | [50,300] | 1.0 | 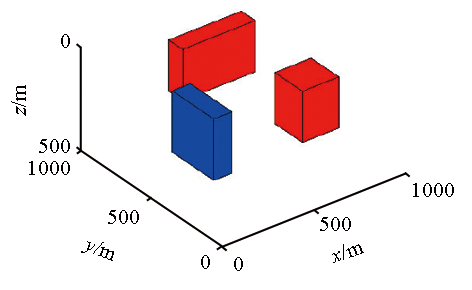 | | 2 | 直立长方体 | [150,250] | [250,550] | [50,300] | -1.0 | | 3 | 直立长方体 | [600,800] | [200,400] | [50,300] | 1.0 |
|
Complex upright model parameters
|

|
Forward results of complex upright model
a—gravity anomaly;b—normalize the balanced vertical derivative (nBVDR);c—normalize the balanced analytical signal amplitude (nBASM)
|

|
Weighted results of correlation tomography for complex upright model
a—imaging results with depth weighted constraints;b—vertical slice at y=300 m(depth weighted constraints);c—horizontal slice at z=200 m(depth weighted constraints);d—imaging results of the method in this article (Wz+VDR weighted);e—vertical slice at y=300 m(Wz+VDR weighted);f—Horizontal slice at z=200 m(Wz+VDR weighted);g—imaging results of the method in this article (Wz+ASM weighted);h—Vertical slice at y=300 m(Wz+ASM weighted);i—horizontal slice at z=200 m(Wz+ASM weighted)
|

| 编号 | 模型名称 | 模型最小埋深/m | 模型最大埋深/m | 剩余密度/
(g·c ) | | | 1 | 倾斜长方体 | 99.547 | 428.725 | 1.0 | 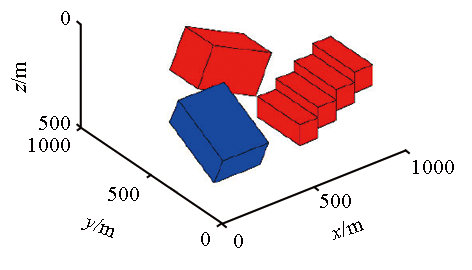 | | 2 | 倾斜长方体 | 99.791 | 383.654 | -1.0 | | 3 | 台阶 | 100.0 | 350.0 | 1.0 |
|
Complex tilt model parameters
|

|
Forward results of complex tilt model
a—gravity anomaly;b—normalize the balanced vertical derivative (nBVDR);c—normalize the balanced analytical signal amplitude (nBASM)
|

|
Weighted results of correlation tomography for complex tilt model
a—imaging results with depth weighted constraints;b—vertical slice at y=250 m(depth weighted constraints);c—horizontal slice at z=250 m(depth weighted constraints);d—imaging results of the method in this article (Wz+VDR weighted);e—vertical slice at y=250 m(Wz+VDR weighted);f—horizontal slice at z=250 m(Wz+VDR weighted);g—imaging results of the method in this article (Wz+ASM weighted);h—vertical slice at y=250 m(Wz+ASM weighted);i—horizontal slice at z=250 m(Wz+ASM weighted)
|
35]
">
|
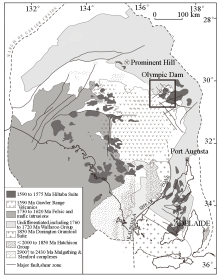
Basement geological map of the Gawler Craton Province [35]
|
36]
">
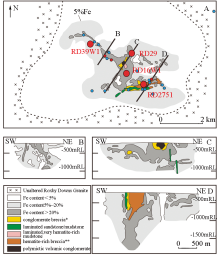
|
Simplified geological map and cross-sectional subsurface structure of the supergiant Olympic Dam breccia complex [36]
|

|
Drill core measured density curve
|

|
Separation results of gravity anomaly at Olympic Dam, Australia
a—gravity anomaly observations;b—regional gravity anomaly;c—residual gravity anomaly
|

|
Weighted results of residual gravity anomaly correlation tomography at Olympic Dam, Australia
a—imaging results of the method in this article (Wz+VDR weighted);b—vertical slice at y=6 063.5 km(Wz+VDR weighted);c—horizontal slice at z=750 m(Wz+VDR weighted);d—imaging results of the method in this article (Wz+ASM weighted);e—vertical slice at y=6 063.5 km(Wz+ASM weighted);f—horizontal slice at z=750 m(Wz+ASM weighted)
|
| [1] |
Patella D. Introduction to ground surface self-potential tomography[J]. Geophysical Prospecting, 1997, 45(4):653-681.

|
| [2] |
Mauriello P, Patella D. Principles of probability tomography for natural-source electromagnetic induction fields[J]. Geophysics, 1999, 64(5):1403-1417.

|
| [3] |
Mauriello P, Patella D. Gravity probability tomography:A new tool for buried mass distribution imaging[J]. Geophysical Prospecting, 2001, 49(1):1-12.

|
| [4] |
Iuliano T, Mauriello P, Patella D. Looking inside Mount Vesuvius by potential fields integrated probability tomographies[J]. Journal of Volcanology and Geothermal Research, 2002, 113(3-4):363-378.

|
| [5] |
许令周, 关继腾, 房文静. 高次导数的概率成像原理[J]. 青岛大学学报:自然科学版, 2003, 16(4):32-36,40.
|
| [5] |
Xu L Z, Guan J T, Fang W J. Theory of probability tomography about second derivative formula[J]. Journal of Qingdao University:Natural Science Edition, 2003, 16(4):32-36,40.
|
| [6] |
王绪本, 毛立峰, 高永才. 电磁导数场概率成像方法研究[J]. 成都理工大学学报:自然科学版, 2004, 31(6):679-684.
|
| [6] |
Wang X B, Mao L F, Gao Y C. Probability tomography of electromagnetic field-derivative method[J]. Journal of Chengdu University of Technology:Science and Technology Edition, 2004, 31(6):679-684.
|
| [7] |
郭良辉, 孟小红, 石磊, 等. 重力和重力梯度数据三维相关成像[J]. 地球物理学报, 2009, 52(4):1098-1106.
|
| [7] |
Guo L H, Meng X H, Shi L, et al. 3-D correlation imaging for gravity and gravity gradiometry data[J]. Chinese Journal of Geophysics, 2009, 52(4):1098-1106.
|
| [8] |
郭良辉, 孟小红, 石磊. 磁异常ΔT三维相关成像[J]. 地球物理学报, 2010, 53(2):435-441.
|
| [8] |
Guo L H, Meng X H, Shi L. 3D correlation imaging for magnetic anomaly ΔT data[J]. Chinese Journal of Geophysics, 2010, 53(2):435-441.
|
| [9] |
Guo L H, Meng X H, Zhang G L. Three-dimensional correlation imaging for total amplitude magnetic anomaly and normalized source strength in the presence of strong remanent magnetization[J]. Journal of Applied Geophysics, 2014, 111:121-128.

|
| [10] |
侯振隆, 王恩德. 基于泰勒级数的重力异常数据快速相关成像[J]. 东北大学学报:自然科学版, 2019, 40(4):563-568.
|
| [10] |
Hou Z L, Wang E D. Fast probability tomography of gravity anomaly data based on Taylor series[J]. Journal of Northeastern University:Natural Science Edition, 2019, 40(4):563-568.
|
| [11] |
孟小红, 刘国峰, 陈召曦, 等. 基于剩余异常相关成像的重磁物性反演方法[J]. 地球物理学报, 2012, 55(1):304-309.
|
| [11] |
Meng X H, Liu G F, Chen Z X, et al. 3D gravity and magnetic inversion for physical properties based on residual anomaly correlation[J]. Chinese Journal of Geophysics, 2012, 55(1):304-309.
|
| [12] |
闫浩飞, 刘国峰. 一种重力异常概率成像的扩展计算[J]. 地球物理学进展, 2014, 29(4):1837-1842.
|
| [12] |
Yan H F, Liu G F. A extension of probability tomography of gravity data[J]. Progress in Geophysics, 2014, 29(4):1837-1842.
|
| [13] |
林涛, 曾昭发, 于平, 等. 基于层源位场的重力及其梯度数据联合相关成像[J]. 世界地质, 2022, 41(1):186-197.
|
| [13] |
Lin T, Zeng Z F, Yu P, et al. Joint probability tomography for gravity and its gradiometry data based on strata-source potential field[J]. World Geology, 2022, 41(1):186-197.
|
| [14] |
Guo L H, Meng X H, Shi L. 3D correlation imaging of the vertical gradient of gravity data[J]. Journal of Geophysics and Engineering, 2011, 8(1):6-12.

|
| [15] |
石磊, 郭良辉, 孟小红. 磁总场异常垂直梯度三维相关成像[J]. 地球物理学进展, 2012, 27(4):1609-1614.
|
| [15] |
Shi L, Guo L H, Meng X H. 3D correlation imaging of the vertical gradient of magnetic total field anomaly[J]. Progress in Geophysics, 2012, 27(4):1609-1614.
|
| [16] |
郑玉君, 侯振隆, 巩恩普, 等. 基于深度加权的多分量重力梯度数据联合相关成像方法[J]. 吉林大学学报:地球科学版, 2020, 50(4):1197-1210.
|
| [16] |
Zheng Y J, Hou Z L, Gong E P, et al. Correlation imaging method with joint multiple gravity gradiometry data based on depth weighting[J]. Journal of Jilin University:Earth Science Edition, 2020, 50(4):1197-1210.
|
| [17] |
马国庆, 牛润馨, 李丽丽, 等. 基于重磁不同阶比值的场源相关成像法研究[J]. 地球物理学进展, 2021, 36(5):2062-2068.
|
| [17] |
Ma G Q, Niu R X, Li L L, et al. Non-degree gradient ratio function of gravity and magnetic data for field-source correlation imaging method study[J]. Progress in Geophysics, 2021, 36(5):2062-2068.
|
| [18] |
赵国兴, 吴燕冈, 王凤刚, 等. 基于窗口数据的重力相关成像[J]. 世界地质, 2016, 35(3):858-864.
|
| [18] |
Zhao G X, Wu Y G, Wang F G, et al. Gravity correlation imaging based on window data[J]. Global Geology, 2016, 35(3):858-864.
|
| [19] |
侯振隆, 郑玉君, 巩恩普, 等. 基于深度加权的重力梯度数据联合相关成像反演[J]. 东北大学学报:自然科学版, 2020, 41(11):1628-1632.
|
| [19] |
Hou Z L, Zheng Y J, Gong E P, et al. Joint correlation imaging inversion with gravity gradiometry data based on depth weighting[J]. Journal of Northeastern University:Natural Science Edition, 2020, 41(11):1628-1632.
|
| [20] |
Li Y G, Oldenburg D W. 3D inversion of magnetic data[J]. Geophysics, 1996, 61(2):394-408.

|
| [21] |
Commer M, Newman G A, Williams K H, et al. 3D induced-polarization data inversion for complex resistivity[J]. Geophysics, 2011, 76(3):F157-F171.

|
| [22] |
Hood P, McClure D J. Gradient measurements in ground magnetic prospecting[J]. Geoghysics, 1965, 30(3):403-410.
|
| [23] |
Bhattacharyya B K. Two-dimensional harmonic analysis as a tool for magnetic interpretation[J]. Geophysics, 1965, 30(5):829-857.

|
| [24] |
Nabighian M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:Its properties and use for automated anomaly interpretation[J]. Geophysics, 1972, 37(3):507-517.

|
| [25] |
Nabighian M N. Toward a three-dimensional automatic interpretation of potential field data via generalized Hilbert transforms:Fundamental relations[J]. Geophysics, 1984, 49(6):780-786.

|
| [26] |
Vella L. Interpretation and modelling,based on petrophysical measurements,of the wirrda well potential field anomaly,South Australia[J]. Exploration Geophysics, 1997, 28(1-2):299-306.

|
| [27] |
Cherry A R, McPhie J, Kamenetsky V S, et al. Linking Olympic Dam and the Cariewerloo Basin:Was a sedimentary basin involved in formation of the world’s largest uranium deposit?[J]. Precambrian Research, 2017, 300:168-180.

|
| [28] |
朱意萍, 高卫华, 马娜, 等. 澳大利亚铀矿的成矿区划、矿床类型及找矿前景[J]. 地质通报, 2014, 33(2/3):172-186.
|
| [28] |
Zhu Y P, Gao W H, Ma N, et al. Metallogenic regionalization,deposit types and ore-search prospect for uranium deposits in Australia[J]. Geological Bulletin of China, 2014, 33(2/3):172-186.
|
| [29] |
McPhie J, Orth K, Kamenetsky V, et al. Characteristics,origin and significance of Mesoproterozoic bedded clastic facies at the Olympic Dam Cu-U-Au-Ag deposit,South Australia[J]. Precambrian Research, 2016, 276:85-100.

|
| [30] |
MacMillan E, Cook N J, Ehrig K, et al. Uraninite from the Olympic Dam IOCG-U-Ag deposit:Linking textural and compositional variation to temporal evolution[J]. American Mineralogist, 2016, 101(6):1295-1320.

|
| [31] |
Williams P J, Barton M D, Johnson D A, et al. Iron oxide copper-gold deposits:Geology,space-time distribution,and possible modes of origin[J]// Economic Geology 100th Anniversary Volume, 2005:371-405.
|
| [32] |
Sillitoe R H. Iron oxide-copper-gold deposits:An Andean view[J]. Mineralium Deposita, 2003, 38(7):787-812.

|
| [33] |
陈超, 潘伟, 董国明, 等. 高精度磁测在IOCG型铁矿勘查中的应用——以智利英格瓦塞铁矿为例[J]. 地质通报, 2020, 39(4):563-573.
|
| [33] |
Chen C, Pan W, Dong G M, et al. The application of high-precision magnetic survey to exploration of IOCG type iron deposits:Exemplified by the Incaguasi iron deposit in Chile[J]. Geological Bulletin of China, 2020, 39(4):563-573.
|
| [34] |
Austin J, Foss C. Rich,attractive and extremely dense:A geophysical review of Australian IOCGs[J]. ASEG Extended Abstracts, 2012, 2012(1):1-4.
|
| [35] |
Direen N G, Lyons P. Regional crustal setting of iron oxide Cu-Au mineral systems of the Olympic Dam region,South Australia:Insights from potential-field modeling[J]. Economic Geology, 2007, 102(8):1397-1414.

|
| [36] |
Kirchenbaur M, Maas R, Ehrig K, et al. Uranium and Sm isotope studies of the supergiant Olympic Dam Cu-Au-U-Ag deposit,South Australia[J]. Geochimica et Cosmochimica Acta, 2016, 180:15-32.

|
| [37] |
杨文采, 施志群, 侯遵泽, 等. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 2001, 44(4):534-541,582.
|
| [37] |
Yang W C, Shi Z Q, Hou Z Z, et al. Discrete wavelet transform for multiple decomposition of gravity anomalies[J]. Chinese Journal of Geophysics, 2001, 44(4):534-541,582.
|
| [38] |
Yang M, Wang W Y, Kim Welford J, et al. 3D gravity inversion with optimized mesh based on edge and center anomaly detection[J]. Geophysics, 2019, 84(3):G13-G23.
|
| [39] |
Zhang S, Yin C C, Cao X Y, et al. DecNet:Decomposition network for 3D gravity inversion[J]. Geophysics, 2022, 87(5):G103-G114.

|
| [1] |
DONG Jian, LI Xiao-Peng, FU Chao, DANG Zhi-Cai, ZHAO Xiao-Bo, ZENG Qing-Bin, HU Xue-Ping, WANG Jin-Hui. Prospecting for concealed skarn iron deposits using the high-precision gravity-magnetic survey method[J]. Geophysical and Geochemical Exploration, 2024, 48(1): 31-39. |
| [2] |
YANG Rong-Xiang, WANG Wan-Yin, CAI Meng-Ke, WANG Ding-Ding, LUO Xin-Gang. A study of tectonic framework of the Qinnan sag in Bohai Basin and its adjacent areas based on satellite gravity anomalies[J]. Geophysical and Geochemical Exploration, 2023, 47(3): 584-596. |
|
|
|
|

