|
|
|
| Inversion of the Rayleigh wave dispersion curves based on the sine-cosine algorithm |
FU Yu1,2( ), AI Han-Bing1,2,3, YAO Zhen-An1,2( ), AI Han-Bing1,2,3, YAO Zhen-An1,2( ), MEI Zhu-Xu1,2, SU Ke-Jia1,2,4 ), MEI Zhu-Xu1,2, SU Ke-Jia1,2,4 |
1. Engineering Research Center for Seismic Disaster Prevention and Engineering Geological Disaster Detection of Jiangxi Province(East China University of Technology),Nanchang 330013,China
2. School of Geophysics and Measurement-control Technology,East China University of Technology,Nanchang 330013,China
3. School of Geophysics and Geomatics, China University of Geosciences(Wuhan),Wuhan 430074,China
4. Research Institute No.270,CNNC,Nanchang 330200,China |
|
|
|
|
Abstract
Rayleigh wave is widely used in engineering investigation and surveys.The inversion of its dispersion curves allows for effectively obtaining stratigraphic information.However,conventional global optimization algorithms in the dispersion curve inversion have a slow convergence rate and low convergence precision and are prone to prematurity.Therefore,this study introduced a novel global optimization algorithm—the sine cosine algorithm (SCA)—to solve the problems mentioned above.Based on the mathematical properties of sine and cosine functions,the SCA can adjust the exploration and development capabilities during the optimization using multiple random parameters and adaptive variables.As a result,it can ensure a high convergence rate and great stability while obtaining high-accuracy solutions.First,the feasibility of the SCA for the dispersion curve inversion was verified using four noise-free models.Then,the strong anti-interference ability of the SCA was proved by adding 15% of random noise to the models.Afterward,it was verified that SCA can yield high-precision,high-stability solutions in the dispersion curve inversion by comparison with the particle swarm optimization (PSO) approach.Finally,the practicability of the SCA was confirmed using seismic data from Arnarbælidi in Iceland and Wyoming in the USA.As indicated by the calculation results of theoretical models and the analysis of measured data,the SCA has a high processing speed,precision,stability,and practicability and thus allows for effective quantitative interpretation of the Rayleigh wave dispersion curves.
|
|
Received: 05 August 2022
Published: 23 January 2024
|
|
|
|
|
|
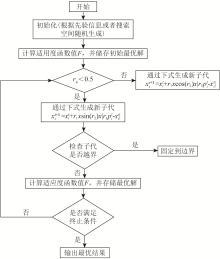
|
Flow chart of SCA
|

| 模型 | 层序号 | 模型参数 | | 搜索范围 | | vs/(m·s-1) | vp/(m·s-1) | ρ/(g·cm-3) | h/m | | vs/(m·s-1) | h/m | | 模型A | 1 | 200 | 780 | 1.9 | 5 | | 100~300 | 2.5~7.5 | | 均匀半空间 | 350 | 850 | 1.9 | ∞ | | 175~525 | ∞ | | 模型B | 1 | 200 | 663 | 1.9 | 2 | | 100~300 | 1~3 | | | 2 | 300 | 995 | 1.9 | 4 | | 150~450 | 2~6 | | 3 | 400 | 1327 | 1.9 | 6 | | 200~600 | 3~9 | | 均匀半空间 | 500 | 1658 | 1.9 | ∞ | | 250~750 | ∞ | | 模型C | 1 | 200 | 663 | 1.9 | 2 | | 100~300 | 1~3 | | | 2 | 160 | 673 | 1.9 | 4 | | 80~240 | 2~6 | | 3 | 300 | 1102 | 1.9 | 6 | | 150~450 | 3~9 | | 均匀半空间 | 400 | 1470 | 1.9 | ∞ | | 200~600 | ∞ | | 模型D | 1 | 150 | 498 | 1.9 | 2 | | 75~225 | 1~3 | | | 2 | 250 | 829 | 1.9 | 4 | | 125~375 | 2~6 | | 3 | 200 | 841 | 1.9 | 6 | | 100~300 | 3~9 | | 均匀半空间 | 400 | 1470 | 1.9 | ∞ | | 200~600 | ∞ | |
|
Model parameter and search space
|

|
Inversion results of noise-free data of model A
a—inverted response compared with the original one;b—inverted shear-wave velocity profile
|

| 模型 | 参数 | 真实值 | | 不含噪声 | | | | 含噪声 | | | 反演均值 | 相对误差/% | 标准差 | | 反演均值 | 相对误差/% | 标准差 | | 模型A | vs1/(m·s-1) | 200 | 199.54 | 0.23% | 1.28 | | 199.69 | 0.15% | 2.71 | | vs2/(m·s-1) | 350 | 347.90 | 0.60% | 5.98 | | 350.79 | 0.23% | 9.07 | | H1/m | 5 | 4.76 | 4.76% | 0.18 | | 4.75 | 5.00% | 0.22 | | 模型B | vs1/(m·s-1) | 200 | 200.94 | 0.47% | 2.52 | | 200.95 | 0.47% | 3.82 | | vs2/(m·s-1) | 300 | 300.75 | 0.25% | 7.42 | | 304.07 | 1.36% | 15.60 | | vs3/(m·s-1) | 400 | 399.19 | 0.20% | 9.34 | | 391.88 | 2.03% | 25.47 | | vs4/(m·s-1) | 500 | 500.19 | 0.04% | 6.03 | | 499.62 | 0.08% | 6.80 | | H1/m | 2 | 2.05 | 2.52% | 0.11 | | 2.02 | 0.83% | 0.16 | | H2/m | 4 | 3.99 | 0.24% | 0.28 | | 3.96 | 1.12% | 0.18 | | H3/m | 6 | 5.59 | 6.76% | 0.53 | | 5.61 | 6.54% | 0.97 | | 模型C | vs1/(m·s-1) | 200 | 197.78 | 1.11% | 9.25 | | 199.90 | 0.05% | 14.71 | | vs2/(m·s-1) | 160 | 161.15 | 0.72% | 4.52 | | 160.55 | 0.34% | 5.35 | | vs3/(m·s-1) | 300 | 286.04 | 4.65% | 32.13 | | 285.78 | 4.74% | 22.89 | | vs4/(m·s-1) | 400 | 397.61 | 0.60% | 13.58 | | 397.19 | 0.70% | 18.96 | | H1/m | 2 | 1.97 | 1.57% | 0.17 | | 1.91 | 4.51% | 0.23 | | H2/m | 4 | 3.86 | 3.58% | 0.43 | | 3.85 | 3.71% | 0.30 | | H3/m | 6 | 5.62 | 6.28% | 1.09 | | 5.51 | 8.16% | 0.43 | | 模型D | vs1/(m·s-1) | 150 | 150.58 | 0.39% | 1.03 | | 149.80 | 0.13% | 2.92 | | vs2/(m·s-1) | 250 | 252.30 | 0.92% | 4.25 | | 251.41 | 0.56% | 7.38 | | vs3/(m·s-1) | 200 | 199.81 | 0.09% | 3.94 | | 202.01 | 1.01% | 4.41 | | vs4/(m·s-1) | 400 | 400.90 | 0.23% | 4.80 | | 400.46 | 0.12% | 6.36 | | H1/m | 2 | 2.03 | 1.41% | 0.07 | | 2.03 | 1.36% | 0.08 | | H2/m | 4 | 3.93 | 1.78% | 0.14 | | 3.98 | 0.44% | 0.24 | | H3/m | 6 | 6.09 | 1.45% | 0.23 | | 5.99 | 0.14% | 0.26 |
|
Inversion results of noise-free and noise-contaminated data with model A,B,C and D
|
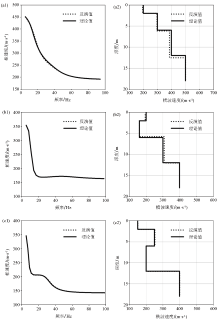
|
Inversion results of noise-free data of model B,C,and D
a1,b1,c1—inverted dispersion curves obtained from model B,C and D respectively;a2,b2,c2—inverted shear-wave velocity profiles obtained from model B,C and D respectively
|
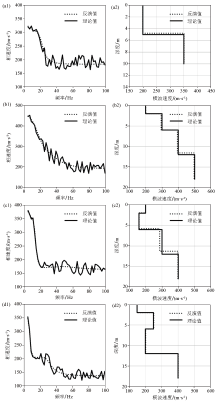
|
Inversion results of noise-contaminated data of model A,B,C,and D
a1,b1,c1,d1—inverted dispersion curves obtained from model A,B,C and D respectively;a2,b2,c2,d2—inverted shear-wave velocity profiles obtained from model A,B,C and D respectively
|
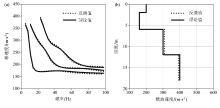
|
Inversion results of model C with multi-modal data
a—inverted responses compared with the original ones;b—inverted shear-wave velocity profile
|

| 参数 | 真实值 | 基阶数据 | 多模数据 | | 反演均值 | 相对误差/% | 标准差 | 反演均值 | 相对误差/% | 标准差 | | vs1/(m·s-1) | 200 | 197.78 | 1.11% | 9.25 | 200.18 | 0.09% | 9.75 | | vs2/(m·s-1) | 160 | 161.15 | 0.72% | 4.52 | 158.98 | 0.64% | 4.60 | | vs3/(m·s-1) | 300 | 286.04 | 4.65% | 32.13 | 308.08 | 2.93% | 21.04 | | vs4/(m·s-1) | 400 | 397.61 | 0.60% | 13.58 | 393.26 | 1.68% | 15.64 | | H1/m | 2 | 1.97 | 1.57% | 0.17 | 1.99 | 0.70% | 0.23 | | H2/m | 4 | 3.86 | 3.58% | 0.43 | 3.99 | 0.28% | 0.30 | | H3/m | 6 | 5.62 | 6.28% | 1.09 | 6.08 | 1.38% | 0.43 |
|
Inversion results of the fundamental-model and multi-model data with model C
|
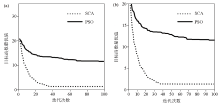
|
Comparison of the convergence rate between SCA and PSO on noise-free data from model D
a—comparison of convergence curves before zooming up;b—comparison of convergence curves after zooming up
|

| 参数 | 真实值 | SCA | PSO | | 反演均值 | 相对误差/% | 标准差 | 反演均值 | 相对误差/% | 标准差 | | vs1/(m·s-1) | 150 | 150.58 | 0.39% | 1.03 | 148.06 | 1.29% | 9.91 | | vs2/(m·s-1) | 250 | 252.30 | 0.92% | 4.25 | 242.06 | 3.18% | 23.34 | | vs3/(m·s-1) | 200 | 199.81 | 0.09% | 3.94 | 176.28 | 11.86% | 37.69 | | vs4/(m·s-1) | 400 | 400.90 | 0.23% | 4.80 | 374.89 | 6.28% | 27.63 | | H1/m | 2 | 2.03 | 1.41% | 0.07 | 1.93 | 3.5% | 0.38 | | H2/m | 4 | 3.93 | 1.78% | 0.14 | 3.72 | 6.86% | 0.97 | | H3/m | 6 | 6.09 | 1.45% | 0.23 | 4.07 | 32.14% | 2.03 |
|
Comparison of the inverted results generated by SCA and PSO
|
29]
">
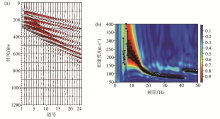
|
Field data(a) and its dispersion image(b) in Arnarb?lidi [29]
|

| 文献估计层厚 | 文献S波速度 | S波速度搜索范围 | 厚度搜索范围 | | /m | /(m·s-1) | /(m·s-1) | /m | | 0.8 | 78 | 60~90 | 0.1~1.5 | | 0.5 | 80 | 70~100 | 0.1~1.5 | | 0.7 | 92 | 80~110 | 0.1~1.5 | | 1.2 | 111 | 100~150 | 0.5~2.0 | | 1.9 | 141 | 120~200 | 0.5~2.0 | | 3.0 | 184 | 150~250 | 2.0~4.0 | | 4.7 | 230 | 200~300 | 3.0~5.5 | | 7.5 | 277 | 250~350 | 6.0~9.0 | | 5.2 | 350 | 300~400 | 4.0~6.0 | | ∞ | 350 | 320~450 | ∞ |
|
Reference inversion model [29]parameters and search range[30] in Arnarb?lidi region
|
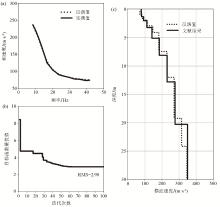
|
Inversion results in Arnarb?lidi region
a—inverted response compared with the original one;b—the minimum value of the objective function changes with the number of iterations;c—inverted shear-wave velocity profile
|
32]
">

|
Field data(a) and its dispersion image(b) in Wyoming [32]
|

| 层数 | vs/(m·s-1) | h/m | 泊松比 | ρ/(g·cm-3) | | 1 | 100~300 | 1~5 | 0.38 | 2.0 | | 2 | 100~400 | 1~5 | 0.38 | 2.0 | | 3 | 100~600 | 1~5 | 0.35 | 2.0 | | 4 | 200~600 | 1~5 | 0.35 | 2.0 | | 5 | 200~800 | 均匀半空间 | 0.30 | 2.0 |
|
Inversion model parameters and search range in Wyoming region[32]
|
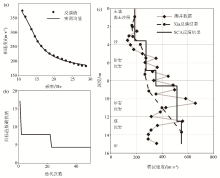
|
Inversion results in Wyoming region
a—inverted response compared with the original one;b—the minimum value of the objective function changes with the number of iterations;c—comparison of the logging data and the inverted shear-wave velocity profile
|
| [1] |
王光文, 王海燕, 李洪强, 等. 面波勘探技术的研究现状及进展[J]. 地球科学前沿, 2019, 9(9):799-815.
|
| [1] |
Wang G W, Wang H Y, Li H Q, et al. Research status and progress of surface wave exploration technology[J]. Frontiers of Earth Science, 2019, 9(9):799-815.
|
| [2] |
伍敦仕, 孙成禹, 林美言. 基于互相关相移的主动源地震面波频散成像方法[J]. 地球物理学进展, 2017, 32(4):1693-1700.
|
| [2] |
Wu D S, Sun C Y, Lin M Y. Activeseismic surface wave dispersion imaging method based on cross-correlation and phase-shifting[J]. Progress in Geophysics, 2017, 32(4):1693-1700.
|
| [3] |
Dal Moro G, Pipan M, Gabrielli P. Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation[J]. Journal of Applied Geophysics, 2007, 61(1):39-55.

|
| [4] |
Sun C Y, Wang Y Y, Wu D S, et al. Nonlinear Rayleigh wave inversion based on the shuffled frog-leaping algorithm[J]. Applied Geophysics, 2017, 14(4):551-558,622.
|
| [5] |
Dorman J, Ewing M. Numerical inversion of seismic surface wave dispersion data and crust-mantle structure in the New York—Pennsylvania area[J]. Journal of Geophysical Research, 1962, 67(13):5227-5241.

|
| [6] |
Gabriels P, Snieder R, Nolet G. In situ measurements of shear-wave velocity in sediments with higher-mode Rayleigh waves[J]. Geophysical Prospecting, 1987, 35(2):187-196.

|
| [7] |
裴江云, 吴永刚, 刘英杰. 近地表低速带反演[J]. 长春地质学院学报, 1994, 24(3):317-320,326.
|
| [7] |
Pei J Y, Wu Y G, Liu Y J. Near surface low velocity zone inversion[J]. Journal of Jilin University:Earth Science Edition, 1994, 24(3):317-320,326.
|
| [8] |
Ganji V, Gucunski N, Nazarian S. Automated inversion procedure for spectral analysis of surface waves[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(8):757-770.

|
| [9] |
宋先海, 肖柏勋, 黄荣荣, 等. 用等厚薄层权重自适应迭代阻尼最小二乘法反演瑞雷波频散曲线[J]. 物探与化探, 2003, 27(3):212-216.
|
| [9] |
Song X H, Xiao B X, Huang R R, et al. The inversion of dispersion curves using self-adaptively iterative damping least square method by combining equal thinner layers with weighting matrix[J]. Geophysical and Geochemical Exploration, 2003, 27(3):212-216.
|
| [10] |
Xia J H, Miller R D, Park C B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 1999, 64(3):691-700.

|
| [11] |
艾东海, 程庆群. 低速软弱夹层二维横波速度结构的OCCAM反演[J]. 工程勘察, 2009, 37(4):87-90.
|
| [11] |
Ai D H, Cheng Q Q. Estimation of 2D s-wave velocity section with low velocity layers by OCCAM algorithm[J]. Geotechnical Investigation and Surveying, 2009, 37(4):87-90.
|
| [12] |
Song X H, Gu H M, Liu J P, et al. Estimation of shallow subsurface shear-wave velocity by inverting fundamental and higher-mode Rayleigh waves[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(7):599-607.

|
| [13] |
Dal Moro G, Pipan M, Gabrielli P. Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation[J]. Journal of Applied Geophysics, 2007, 61(1):39-55.

|
| [14] |
Arai H, Tokimatsu K. S-wave velocity profiling by joint inversion of microtremor dispersion curve and horizontal-to-vertical (H/V) spectrum[J]. Bulletin of the Seismological Society of America, 2005, 95(5):1766-1778.

|
| [15] |
石耀霖, 金文. 面波频散反演地球内部构造的遗传算法[J]. 地球物理学报, 1995, 38(2):189-198.
|
| [15] |
Shi Y L, Jin W. Genetic algorithms inversion of lithospheric structure from surface wave dispersion[J]. Chinese Journal of Geophysics, 1995, 38(2):189-198.
|
| [16] |
Yamanaka H, Ishida H. Application of genetic algorithms to an inversion of surface-wave dispersion data[J]. Bulletin of the Seismological Society of America, 1996, 86(2):436-444.

|
| [17] |
张碧星, 肖柏勋, 杨文杰, 等. 瑞利波勘探中“之”形频散曲线的形成机理及反演研究[J]. 地球物理学报, 2000, 43(4):557-567.
|
| [17] |
Zhang B X, Xiao B X, Yang W J, et al. Mechanism of Zigzag dispersion curves in Rayleigh exploration and its’inversion study[J]. Chinese Journal of Geophysics, 2000, 43(4):557-567.
|
| [18] |
Martínez M D, Lana X, Olarte J, et al. Inversion of Rayleigh wave phase and group velocities by simulated annealing[J]. Physics of the Earth and Planetary Interiors, 2000, 122(1-2):3-17.

|
| [19] |
Beaty K S, Schmitt D R, Sacchi M. Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure[J]. Geophysical Journal International, 2002, 151(2):622-631.

|
| [20] |
Calderón-Macías C, Luke B. Improved parameterization to invert Rayleigh-wave data for shallow profiles containing stiff inclusions[J]. Geophysics, 2007, 72(1):U1-U10.
|
| [21] |
Pei D H, Louie J N, Pullammanappallil S K. Application of simulated annealing inversion on high-frequency fundamental-mode Rayleigh wave dispersion curves[J]. Geophysics, 2007, 72(5):R77-R85.
|
| [22] |
Lu Y X, Peng S P, Du W F, et al. Rayleigh wave inversion using heat-bath simulated annealing algorithm[J]. Journal of Applied Geophysics, 2016, 134:267-280.

|
| [23] |
Song X H, Tang L, Lyu X C, et al. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves[J]. Journal of Applied Geophysics, 2012, 84:1-13.

|
| [24] |
蔡伟, 宋先海, 袁士川, 等. 利用粒子群优化算法快速、稳定反演瑞雷波频散曲线[J]. 石油地球物理勘探, 2018, 53(1):25-34,4-5.
|
| [24] |
Cai W, Song X H, Yuan S C, et al. Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization[J]. Oil Geophysical Prospecting, 2018, 53(1):25-34,4-5.
|
| [25] |
Mirjalili S. SCA:A sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96:120-133.

|
| [26] |
杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6):1217-1227,1172.
|
| [26] |
Yang B, Xiong Z Q, Zhang D Z, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6):1217-1227,1172.
|
| [27] |
于东凯, 宋先海, 张学强, 等. 蚱蜢算法在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2019, 54(2):288-301,236.
|
| [27] |
Yu D K, Song X H, Zhang X Q, et al. Rayleigh wave dispersion inversion based on grasshopper optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(2):288-301,236.
|
| [28] |
高旭, 于静, 李学良, 等. 自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2021, 56(4):745-757,671-672.
|
| [28] |
Gao X, Yu J, Li X L, et al. Rayleigh wave dispersion curve inversion based on adaptive weight dragonfly algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4):745-757,671-672.
|
| [29] |
Ólafsdóttir E Á. Multichannel analysis of surface waves for assessing soil stiffness[D]. University of Iceland, 2016.
|
| [30] |
符健. 基于改进非线性算法的瑞利波多模式频散曲线反演研究[D]. 西安: 长安大学, 2019.
|
| [30] |
Fu J. Research on multimodal Rayleigh wave dispersion curve inversion based on improved nonlinear algorithms[D]. Xi'an: Chang'an University, 2019.
|
| [31] |
Xia J H. Estimation of near-surface shear-wave velocities and quality factors using multichannel analysis of surface-wave methods[J]. Journal of Applied Geophysics, 2014, 103:140-151.

|
| [32] |
蔡伟, 宋先海, 袁士川, 等. 基于萤火虫和蝙蝠群智能算法的瑞雷波频散曲线反演[J]. 地球物理学报, 2018, 61(6):2409-2420.
|
| [32] |
Cai W, Song X H, Yuan S C, et al. Inversion of Rayleigh wave dispersion curves based on firefly and bat algorithms[J]. Chinese Journal of Geophysics, 2018, 61(6):2409-2420.
|
| [1] |
XIANG Zhu-Bao, ZHANG Da-Zhou, ZHU De-Bing, LI Ming-Zhi, XIONG Zhang-Qiang. Exploring the Rayleigh wave propagation characteristics in different aggregate concrete models[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1226-1235. |
| [2] |
LI Xin-Xin, LI Jiang, LIU Jun, SHEN Hong-Yan. Processing of the seismic Rayleigh wave data of coalfields based on the improved phase-shift method[J]. Geophysical and Geochemical Exploration, 2022, 46(6): 1470-1476. |
|
|
|
|

