|
|
|
| Application of iTilt-Euler deconvolution in gravity data processing and fault system interpretation |
CHEN Qing1,2( ), SUN Shuai1, DING Cheng-Yi1, HUANG Xiao-Yu1, CHEN Hao3, SHEN Peng1, LUO Gang1, WEI Yao-Cong1 ), SUN Shuai1, DING Cheng-Yi1, HUANG Xiao-Yu1, CHEN Hao3, SHEN Peng1, LUO Gang1, WEI Yao-Cong1 |
1. Department of Earth Science, School of Petroleum and Natural Gas Engineering, Chongqing University of Science and Technology, Chongqing 401331, China
2. Chongqing Key Laboratory of Complex Oil and Gas Exploration and Development, Chongqing 401331, China
3. Chongqing 208 Geoenvironmental Engineering Survey and Design Institute Co., Ltd., Chongqing 400700, China |
|
|
|
|
Abstract In order to improve the convergence and stability of Euler inverted results, the iTilt-Euler method, which do not depend on the structure index, is used for the calculation. Furthermore, the data points are constrained by the peak values of tilt angle of the total horizontal derivative (TAHG) to optimize the solutions. The method has been demonstrated with synthetic and real data. For synthetic data, the convergence of iTilt-Euler inversion results constrained by the TAHG method is improved effectively to detect the fault structures with deeper depth. Application to gravity data for the ANZA basin in Kenya shows that the iTilt-Euler inversion results constrained by peak values of TAHG have good continuity. The results distribute generally along NW direction, followed by NE direction, and these characteristics are consistent with the identifying features of fault in the second-order vertical derivative and total horizontal derivative anomaly maps. Furthermore, the inversion depth results show that the solutions along NW direction are extend to large scale and with higher values, which is reflected as a basement fault that controls the boundary of the main tectonic units in the study area and usually cut by the superficial faults with NE extension. It is worth noting that a large deep fault with NNE extension is developed in the southeast of the study area, which cuts the north-west direction and the north-east direction fault. It is speculated that it may control the southeast boundary of the regional tectonic unit. We can conclude that the iTilt-Euler deconvolution combined with the peak constraint method can provide a reliable method for fault system interpretation, and has good practicability.
|
|
Received: 18 May 2021
Published: 21 December 2021
|
|
|
|
|
|

|
Gravity anomaly forward modeling of conbined model (the black dotted lines represent the actual edges of the models)
a—sketch representation of combined model;b—gravity anomaly of combined model;c—random noise with amplitude equal to 2% of maimum data amplitude was added to the gravity anomaly of combined model
|

| 模型体 | 中心点坐标/km | 长度/km | 宽度/km | 顶面埋深/km | 厚度/km | 旋转角度/(°) | | 1 | (-18,-34) | 52 | 20 | 1 | 2 | -45 | | 2 | (-18,34) | 52 | 20 | 2 | 2 | 45 | | 3 | (36,0) | 120 | 16 | 3 | 3 | 0 |
|
Combined model parameters
|

|
Results of Euler deconvolution based on the combined model without noise
a—tilt angle;b—estimated results from the Tilt-Euler; c—improved tilt angle; d—estimated results from the iTilt-Euler; e—total horizontal derivative of tilt angle; f—estimated results from the iTilt-Euler under the peak constraint of total horizontal derivative of tilt angle
|

|
Results of Euler deconvolution based on the combined model with 2% Gaussian noise
a—tilt angle; b—estimated results from the Tilt-Euler; c—improved tilt angle; d—estimated results from the iTilt-Euler; e—total horizontal derivative of tilt angle; f—estimatedresults fromthe iTilt-Euler under the peak constraint of total horizontal derivative of tilt angle
|
|
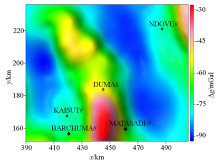
The map of the Bouguer gravity anomaly in study area
|
|
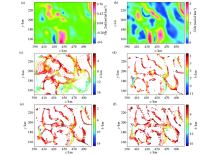
Euler deconvolution results of gravity anomalies in the study area
a—second order derivative; b—total horizontal derivative; c—estimated results from conventional Euler deconvolution(N=0.5); d—estimated results fromTilt-Euler method; e—estimated results from iTilt-Euler method; f—estimated results from iTilt-Euler method under the peak constraint
|

|
The distribution of fault structure in study area
|
| [1] |
Thompson D T. EULDPH—A new technique for making computer-assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47(1):31-37.

|
| [2] |
Reid A B, Allsop J M, Granser H, et al. Magnetic interpretation in three dimensions using Euler deconvolution[J]. Geophysics, 1990, 55(1):80-91.

|
| [3] |
姚长利, 管志宁, 吴其斌, 等. 欧拉反演方法分析及实用技术改进[J]. 物探与化探, 2004, 28(2):150-155.
|
| [3] |
Yao C L, Guan Z N, Wu Q B, et al. An analysis of Euler deconvolution and its improvement[J]. Geophysical and Geochemical Exploration, 2004, 28(2):150-155.
|
| [4] |
Hsu S K. Imaging magnetic sources using Euler’s equation[J]. Geophysical Prospecting, 2002, 50:15-25.

|
| [5] |
Salem A, Ravat D. A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data[J]. Geophysics, 2003, 68(6):1952-1961.

|
| [6] |
Salem A, Smith R. Generalized magnetic tilt-Euler deconvolution[C]// SEG Expanded Abstracts, 2007: 790-794.
|
| [7] |
范美宁, 江裕标, 张景仙. 不同数据用于欧拉方程的模型计算[J]. 地球物理学进展, 2008, 23(4):1250-1253.
|
| [7] |
Fan M N, Jiang Y B, Zhang J X. Model calculation of Euler’s equation for different data types[J]. Progress in Geophysics, 2008, 23(4):1250-1253.
|
| [8] |
Ma G Q. The application of extended Euler deconvolution method in the interpretation of potential field data[J]. Journal of Applied Geophysics, 2014, 107(8):188-194.

|
| [9] |
Neil C, Whaler K A, Reid A B. Extensions to Euler’s method for three-dimensional potential field interpretation[C]// 53rd EAEG meeting, Florence, Expanded Abstracts, 1991:416-417.
|
| [10] |
Fairhead J D, Bennett K J, Gordon D R H, et al. Euler: beyond the “Black Box”[C]// SEG Expanded Abstracts, 1994: 422-424.
|
| [11] |
Keating P B. Weighted Euler deconvolution of gravity data[J]. Geophysics, 1998, 63(5):1595-1603.

|
| [12] |
范美宁, 孙运生, 田庆君. 关于欧拉反褶积方法计算中的一点改进[J]. 物探化探计算技术, 2005, 27(2):171-174.
|
| [12] |
Fan M N, Sun Y S, Tian Q J. An improvement on calculation of Euler deconvolution[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2005, 27(2):171-174.
|
| [13] |
Davis K, Li Y. Enhancement of depth estimation techniques with amplitude analysis[C]// SEG Expanded Abstracts, 2009: 908-912.
|
| [14] |
周勇, 曹书锦, 侯萍萍, 等. 重力场欧拉反褶积最优解提取[J]. 物探化探计算技术, 2017, 39(5):598-604.
|
| [14] |
Zhou Y, Cao S J, Hou P P, et al. Extraction optimal solution of Euler deconvolution for gravity data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2017, 39(5):598-604.
|
| [15] |
Gerovska D, Araúzo-Bravo M J. Automatic interpretation of magnetic data based on Euler deconvolution with unprescribed structural index[J]. Computers & Geosciences, 2003, 29(8):949-960.

|
| [16] |
Ugalde H, Morris B. Cluster analysis of Euler deconvolution solutions: New filtering techniques and actual link to geological structure[C]// SEG Expanded Abstracts, 2008:794-798.
|
| [17] |
Salem A, Williams S, Fairhead D, et al. Interpretation of magnetic data using tilt-angle derivatives[J]. Geophysics, 2008, 73(1):L1-L10.

|
| [18] |
Beiki M. TSVD analysis of Euler deconvolution to improve estimating magnetic source parameters: An example from the Sele area, Sweden[J]. Journal of Applied Geophysics, 2013, 90:82-91.

|
| [19] |
Barbosa V C F, Silva J B C, Medeiros W E. Making Euler deconvolution applicable to small ground magnetic surveys[J]. Journal of Applied Geophysics, 2000, 43(1):55-68.

|
| [20] |
郭志宏. 航磁及梯度数据正反演解释方法技术实用化改进及应用[D]. 北京:中国地质大学(北京), 2004.
|
| [20] |
Guo Z H. The practical improvement of forward and inversion technique on aeromagnetic gradient data and its application[D]. Beijing:China University of Geoscience (Beijing), 2004.
|
| [21] |
鲁宝亮, 范美宁, 张原庆. 欧拉反褶积中构造指数的计算与优化选取[J]. 地球物理学进展, 2009, 24(3):1027-1031.
|
| [21] |
Lu B L, Fan M N, Zhang Y Q. The calculation and optimization of structure index in Euler deconvolution[J]. Progress in Geophysics, 2009, 24(3):1027-1031.
|
| [22] |
曹书锦, 朱自强, 鲁光银. 基于自适应模糊聚类分析的重力张量欧拉反褶积解[J]. 中南大学学报:自然科学版, 2012, 43(3):1033-1039.
|
| [22] |
Cao S J, Zhu Z Q, Lu G Y. Gravity tensor Euler Deconvolution solutions based on adaptive fuzzy cluster analysis[J]. Journal of Central South Unirersity:Science and Teclmology, 2012, 43(3):1033-1039.
|
| [23] |
Miller H G, Singh V. Potential field tilt—a new concept for location of potential field sources[J]. Journal of Applied Geophysics, 1994, 32(2-3):213-217.

|
| [24] |
王想, 李桐林. Tilt梯度及其水平导数提取重磁源边界位置[J]. 地球物理学进展, 2004, 19(3):625-630.
|
| [24] |
Wang X, Li T L. Locating the boundaries of magnetic or gravity sources with Tdr and Tdr-Thdr methods[J]. Progress in Geophysics, 2004, 19(3):625-630.
|
| [25] |
王万银, 邱之云, 杨永, 等. 位场边缘识别方法研究进展[J]. 地球物理学进展, 2010, 25(1):196-210.
|
| [25] |
Wang W Y, Qiu Z Y, Yang Y, et al. Some advances in the edge recognition of potential field[J]. Progress in Geophysics, 2010, 25(1):196-210.
|
| [26] |
刘鹏飞, 刘天佑, 杨宇山, 等. Tilt梯度算法的改进与应用:以江苏韦岗铁矿为例[J]. 地球科学:中国地质大学学报, 2015, 40(12):2091-2102.
|
| [26] |
Liu P F, Liu T Y, Yang Y S, et al. An improved tilt angle method and its application: A case of Weigang iron ore deposit, Jiangsu[J]. Earth Science-Journal of China University of Geosciences, 2015, 40(12):2091-2102.
|
| [27] |
Huang L, Zhang H L, Sekelania S, et al. An improved Tilt-Euler deconvolution and its application on a Fepolymetallic deposit[J]. Ore Geology Reviews, 2019, 114:103-114.
|
| [28] |
Ferreira F J F, de Souza J, de B. e S. Bongiolo A, et al. Enhancement of the total horizontal gradient of magnetic anomalies using the tilt angle[J]. Geophysics, 2013, 78(3):J33-J41.

|
| [29] |
Greene L C, Richards D R, Johnson R A. Crustal structure and tectonic evolution of the Anza rift, northern Kenya[J]. Tectonophysics, 1991, 197:203-211.

|
| [30] |
Bosworth W, Morley C K. Structural and stratigraphic evolution of the Anza rift, Kenya[J]. Tectonophysics, 1994, 236:93-115.

|
| [31] |
西安石油大学. 肯尼亚ANZA盆地9、10A区块重磁震联合解释报告[R]. 2007.
|
| [31] |
Xi'an Shiyou University. The research of integrated interpretation of gravity, aeromagnetics and seismic data of block 9 and 10A of ANZA basin in Kenya_Atlas contents[R]. 2007.
|
| [1] |
YANG Rong-Xiang, WANG Wan-Yin, CAI Meng-Ke, WANG Ding-Ding, LUO Xin-Gang. A study of tectonic framework of the Qinnan sag in Bohai Basin and its adjacent areas based on satellite gravity anomalies[J]. Geophysical and Geochemical Exploration, 2023, 47(3): 584-596. |
| [2] |
WANG Run-Sheng, WU Bin, ZHANG Hai-Rui, YU Jia-Bin, DONG Yan-Long, GUO Guo-Qiang, KANG Yi-Ming. Gravity field characteristics and boundaries of geotectonic units on the northeastern margin of the Linyi uplift, Shandong Province[J]. Geophysical and Geochemical Exploration, 2023, 47(2): 279-289. |
|
|
|
|

