地—井直流电法在路基岩溶勘探中的应用

doi:10.11720/wtyht.2025.1407

地—井直流电法在路基岩溶勘探中的应用

余小晴^,¹, 温金豪^,²

1.江西赣粤高速公路股份有限公司, 江西南昌 330006

2.东华理工大学地球物理与空间探测学院, 江西南昌 330013

Application of the surface-to-borehole direct current method for subgrade investigations in karst terrain

YU Xiao-Qing^,¹, WEN Jin-Hao^,²

1. Jiangxi Ganyue Expressway Co. Ltd., Nanchang 330006, China

2. School of Geophysics and Space Exploration, East China University of Technology, Nanchang 330013, China

通讯作者: 温金豪(1999-),男,硕士研究生在读,研究方向为数值模拟与反演。Email:2681531617@qq.com

第一作者: 余小晴(1982-),男,硕士,研究方向为路基岩土。Email:136804603@qq.com

收稿日期: 2024-10-10 修回日期: 2024-11-18

基金资助:

江西省交通运输厅项目“孔底岩溶探测装备与判读技术研究”(2022H0025)
核资源与环境国家重点实验室联合创新基金项目(2022NRE-LH-08)

Received: 2024-10-10 Revised: 2024-11-18

摘要

在岩溶路基勘探工程中,地表高密度直流电阻率法的应用面临挑战:一方面,电极阵列长度的局限性限制了该方法的有效勘探深度;另一方面,随着勘探深度的递增,深部可获得的电流分布信息随之递减,导致该方法的分辨能力逐渐减弱,尤其难以精确预测深部的小规模岩溶发育区域。为解决这一问题,本文提出了一种解决方案,即在传统地表高密度直流电阻率法观测的基础上,引入井中电极,实现“地—井”直流电阻率数据采集。该策略旨在通过增设井中电极来增加并获取深部电流分布信息,从而达到增加局部有效勘探深度和提高反演结果分辨率的效果。为评估“地—井”直流电阻率观测方法在获取深部岩溶信息方面的效果,本文首先采用数值模拟方法进行深入分析,随后,通过岩溶路基的实测数据反演结果,进一步论证了该方法的实际应用价值与有效性。研究结果显示,引入井中电极的高密度直流电阻率测量技术能够显著提升对深部异常体的识别分辨率,为打破高密度电法在深部岩溶勘探中的局限性提供了有效路径。

关键词： 岩溶; 路基勘探; 地—井直流电法; 正则化反演

Abstract

In karst subgrade exploration engineering, the application of the surface multi-electrode resistivity method faces challenges: on the one hand, the limitation of electrode array length constrains the effective exploration depth of this method; on the other hand, as the exploration depth increases, the available current distribution information from deeper layers decreases, resulting in a gradual weakening of the method's resolution capability, particularly in accurately predicting small-scale karst development areas at depth. To address this issue, the article proposes a solution: introducing wellbore electrodes on the basis of traditional surface multi-electrode resistivity observations to achieve “surface-to-wellbore” resistivity data acquisition. This strategy aims to increase and obtain deep current distribution information by adding wellbore electrodes, thereby enhancing the local effective exploration depth and improving the resolution of inversion results. To evaluate the effectiveness of the “surface-to-wellbore” resistivity observation method in obtaining deep karst information, the article first conducts an in-depth analysis using numerical simulation methods. Subsequently, the practical application value and effectiveness of this method are further demonstrated through inversion results based on measured data from karst subgrades. The research results show that the multi-electrode resistivity measurement technique with wellbore electrodes can significantly improve the resolution for identifying deep anomalies, providing an effective path to overcome the limitations of multi-electrode resistivity methods in deep karst exploration.

Keywords： karst; subgrade exploration; surface-borehole direct current method; regularization for inversion

PDF (2898KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

余小晴, 温金豪. 地—井直流电法在路基岩溶勘探中的应用[J]. 物探与化探, 2025, 49(6): 1459-1466 doi:10.11720/wtyht.2025.1407

YU Xiao-Qing, WEN Jin-Hao. Application of the surface-to-borehole direct current method for subgrade investigations in karst terrain[J]. Geophysical and Geochemical Exploration, 2025, 49(6): 1459-1466 doi:10.11720/wtyht.2025.1407

0 引言

岩溶对工程的危害主要体现为工程基础悬空,即岩溶无法承受其上部的载荷,从而引发陷落或突然性坍塌,进而导致地表工程结构被破坏。地下岩溶发育给公路工程建设与安全运行带来了极大挑战^[1-3]。因此,在岩溶地区的公路建设中,对岩溶路基进行详尽的勘查显得尤为重要。精确探测路基岩溶的发育情况,不仅能够为路基设计提供精确的地质数据支持,还能够有效预防在施工过程中的突发事件,确保施工过程的顺利进行,同时降低成本、提高效率,以保障工程项目的质量和安全。

鉴于岩溶是一种隐蔽性灾害地质体构造,其特征表现为岩溶发育的不确定性、随机性和难以直观探测的隐蔽性,单纯依赖钻探技术进行岩溶勘查是不切实际的。首要原因在于,工程项目要兼顾经济效益,钻孔的布设密度度有限,因此存在未能覆盖所有岩溶洞穴发育区域的风险;其次,即便通过钻孔手段发现了岩溶洞穴发育区域,也难以定量地确定其规模、形态。地球物理方法凭借其覆盖区域广、成本低、工作效率高等优势,成为了工程地质勘探必要的辅助手段。常用的地球物理岩溶探测方法主要有直流电阻率法^[4-6]、浅层地震^[7]、地质雷达^[8-9]、电磁波层析成像^[10]等。其中,直流电阻率法是利用地壳中不同介质间导电性差异,通过观测人工建立的地下稳定电流场的分布规律,来区分地下不同电阻率特征的区域,以及解决有关地质问题的地球物理勘探方法。该方法广泛应用于水文地质调查、工程勘探等领域^[11-12],还具有抗干扰能力强、野外采集一次性布极、自动化快速采集大量数据、工作效率高等优点^[13]。将该方法应用于岩溶勘探,能起到事半功倍的效果^[14]。高密度直流电阻率法探测岩溶的基础是地下不同介质的电阻率差异,即含水岩溶发育区通常呈现低电阻率特征,不含水岩溶发育区通常呈现高电阻率特征^[15],通过反演高密度直流电阻率观测数据可获得地下电阻率的分布情况,即可根据电阻率差异圈定地下岩溶发育状况。地表高密度直流电阻率法的有效勘探深度与测线长度直接相关,在实际的工程勘探中,测线长度易受到地表地形条件的限制,往往导致勘探深度达不到工程需求的情况;另外,随着勘探深度的深加,该方法对异常的分辨能力会逐渐降低。因此,采用地表高密度电阻率法很难对具有一定深度且规模较小的岩溶发育区进行有效地勘探。考虑到上述因素,本文在地表直流电阻率法的基础上引入井中电极实现“地—井”直流电阻率法勘探,通过引入井中电极提高深部电流分布水平,进而提高探测深度与分辨率。

为了验证引入井中电极的直流电阻率法能有效提高直流电法勘探深部异常的分辨率,笔者在非结构化网格反演研究^[16]的基础上,开展了该方法在路基岩溶勘探中的应用研究。首先推导了“地—井”直流电阻率的正演与正则化目标函数反演公式;然后,通过数值模拟岩溶发育,并根据反演结果分析了“地—井”直流电阻率法在路基岩溶探测的优势;最后,将该方法应用于岩溶路基的实测数据反演中,验证了该方法的实用性与有效性。

1 “地—井”直流电阻率勘探原理

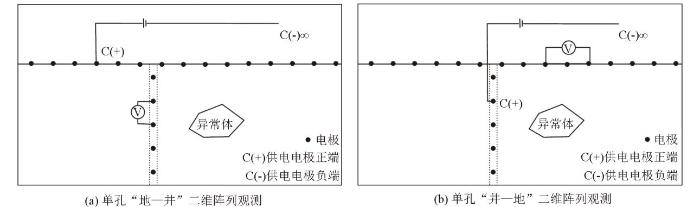
“地—井”直流电阻率法是在地表直流电阻率法工作的基础上,充分利用钻孔布设井中电极,将地表电极与孔中电极视为一个整体,通过特定的电极组合进行观测,最终形成“地—井”直流电阻率法观测数据集。需要注意的是,与地表装置相比,井中电极的视电阻率的定义与地表装置有所不同,也不能像地表装置那样定义为视深度。因此,在数据的后续解释与处理方面,“地—井”直流电阻率法更依赖于反演技术,以确保勘探结果的准确性和可靠性。常见的“地—井”阵列观测勘探示意如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 地—井高密度电法勘探示意

Fig.1 Schematic diagram of multi-electrode resistivity method with well observations

1.1 “地—井”直流电阻率法有限元2.5D正演

采用非结构化有限元算法进行“地—井”直流电阻率2.5D正演^[17]。在二维条件下,假设地质体走向沿y轴正方向,在A位置存在一个电流强度为I的点电流源,其边值问题可表示为:

(1)$　\left\{\begin{array}{ll}\Delta ·\left(\sigma \Delta U\right)-{k}^{2}\sigma U=-I\delta \left(A\right)& \in \Omega,\\ \frac{\partial U}{\partial n}=0& \in {\Gamma }_{s},\\ \frac{\partial U}{\partial n}+k\frac{{K}_{1}\left(kr\right)}{{K}_{0}\left(kr\right)}cos(r,n)U=0& \in {\Gamma }_{\infty }。\end{array}\right.$

式中:U(x,k,z)表示傅氏域电位;δ(A)为与供电点源A有关的狄拉克函数;σ 为电导率;I为电流强度;n为边界外法线矢量;r为位置矢量;k为波数;K₀、K₁分别为零阶和一阶第二类贝塞尔函数;Γ_s表示地面边界;Γ_∞表示无穷远边界。则式(1)边值问题对应的二维等价变分问题表示为:

(2)$\left\{\begin{array}{l}F\left(U\right)={\int }_{\Omega }\left[\frac{1}{2}\sigma {\left(\Delta \right.U)}^{2}+\frac{1}{2}\sigma {\left(kU\right)}^{2}-I\delta \left(A\right)U\right],\\ d\Omega +\frac{1}{2}{\int }_{{\Gamma }_{\infty }}\sigma k\frac{{K}_{1}\left(kr\right)}{{K}_{0}\left(kr\right)}cos(r,n){U}^{2}d\Gamma,\\ \delta F\left(U\right)=0。\end{array}\right.$

采用有限单元法^[18]求解式(2)极值问题,可得线性方程组:

(3)$KU=P,$

式中:K为刚度矩阵;P为描述源分布的向量;U为求解各个节点的傅氏变换的电位,最后经过傅氏反变换可得各节点的电位。地表与井中视电阻率计算方式相似,通过镜像法计算考虑井中电极的视电阻率为ρ_a:

(4)${\rho }_{a}={K}_{a}\frac{\Delta {u}_{AB}^{MN}}{I},$

式中:K_a为装置系数;Δ${u}_{AB}^{MN}$为在A、B两点供电,M、N测量所得的电位差。则装置系数K_a为:

(5)${K}_{a}=\frac{4\pi }{\frac{1}{{r}_{AM}}+\frac{1}{{r}_{A\text{'}M}}-\frac{1}{{r}_{AN}}+\frac{1}{{r}_{A\text{'}N}}-\frac{1}{{r}_{BM}}-\frac{1}{{r}_{B\text{'}M}}+\frac{1}{{r}_{BN}}+\frac{1}{{r}_{B\text{'}N}}},$

式中:A'、B'为A、B两点对应的虚电源;r_AM为A与M之间的距离^[16]。

1.2 “地—井”直流电阻率法正则化反演

通过正则化反演技术^[19],建立“地—井”直流电阻率反演正则化目标函数:

(6)$\begin{array}{l}\varphi \left(m\right)=\Vert {W}_{d}[{d}^{obs}-f(m\left)\right]{\Vert }_{2}^{2}+\mu ‖{W}_{m}(m-\\ {m}^{ref}){\Vert }_{2}^{2},\end{array}$

式中:模型参数向量m表示每个单元中的电阻率值;μ为初始正则化因子;f(m)为预测模型的正演响应数据;d^obs为观测数据;W_d数据协方差矩阵,其形式如下:

(7)${W}_{d}=diag\left(\frac{1}{{\sigma }_{1}+\zeta },\frac{1}{{\sigma }_{i}+\zeta },...,\frac{1}{{\sigma }_{N}+\zeta }\right),$

式中:ζ为极小的正实数,确保数据协方差矩阵有效;σ_i为数据假设方差;N为观测数据的个数。拟合差函数采用最小结构稳定因子,则式(6)中右侧第二项可具体表示为:

(8)$\begin{array}{l}\Vert {W}_{m}(m-{m}^{ref}){\Vert }_{2}^{2}={\alpha }_{s}\int (m-{m}^{ref}{)}^{2}dv+\\ {\alpha }_{x}\int {\left(\frac{\partial m}{\partial x}\right)}^{2}dv+{\alpha }_{z}\int {\left(\frac{\partial m}{\partial z}\right)}^{2}dv,\end{array}$

式中:α_s、α_x、α_z为比例系数。后文中,该项采用Zhdanov给出模型约束函数ϕ_m(m)的统一形式^[19]。式(8)中,m^ref为参考模型;W_m为最小结构模型加权矩阵;可表示为:

(9)${W}_{m}={\alpha }_{s}E+{\alpha }_{x}{W}_{x}+{\alpha }_{z}{W}_{z},$

式中:E为单位矩阵;W_x和W_z分别为水平与垂直方向粗糙度矩阵^[20]。本文比例系数设置为α_s∶α_x∶α_z=10^-3∶1∶1。

采用高斯—牛顿法优化求解目标函数式(6)。假设第n+1次迭代,对正演算子f(m⁽ⁿ⁺¹⁾)进行泰勒展开,则目标函数第n+1次的迭代结果为:

(10)$\begin{array}{l}{\varphi }^{(n+1)}\left(m\right)=\Vert {W}_{d}[{d}^{obs}-f({m}^{\left(n\right)})-{J}^{\left(n\right)}\Delta {m}^{\left(n\right)}]{\Vert }_{2}^{2}+\\ \mu ‖{W}_{m}[{m}^{\left(n\right)}+\Delta {m}^{\left(n\right)}-{m}^{ref}]{\Vert }_{2}^{2},\end{array}$

式中:m⁽ⁿ⁾为第n次模型参数向量;Δm⁽ⁿ⁾为第n+1次模型改变量;J⁽ⁿ⁾为第n次直流电阻率数据对模型参数的偏导数矩阵。将目标函数第n+1次迭代方程ϕ⁽ⁿ⁺¹⁾(m)对Δm⁽ⁿ⁾进行求导并取0,可得以下高斯—牛顿方程:

(11)$\begin{array}{l}[{J}^{\left(n\right)T}{{W}^{T}}_{d}{W}_{d}{J}^{\left(n\right)}+\mu {{W}^{T}}_{m}{W}_{m}]\Delta {m}^{\left(n\right)}={J}^{\left(n\right)T}{{W}^{T}}_{d}{W}_{d}\\ [{d}^{obs}-{f}^{\left(n\right)}(m\left)\right]-\mu {W}_{m}^{T}{W}_{m}[{m}^{\left(n\right)}-{m}^{ref}],\end{array}$

采用稳定双共轭梯度法(BICGSTAB)^[21]对式(11)进行最优化求解得最优模型改变量参数Δm⁽ⁿ⁾,再根据搜索步长得到新的模型参数,更新的模型为:

(12)${m}^{(n+1)}={m}^{\left(n\right)}+\eta \Delta {m}^{\left(n\right)},$

其中:η为沿模型改进量;Δm⁽ⁿ⁾的搜索步长,采用线性搜索,表示为:

(13)$\eta =\frac{\Delta {m}^{\left(n\right)T}{b}^{\left(n\right)}}{\Delta {m}^{\left(n\right)T}{A}^{\left(n\right)}\Delta {m}^{\left(n\right)}+\xi },$

(14)$\begin{array}{l}b={J}^{\left(n\right)T}{{W}^{T}}_{d}{W}_{d}[{d}^{obs}-{f}^{\left(n\right)}(m\left)\right]-\mu {{W}^{T}}_{m}\\ {W}_{m}({m}^{\left(n\right)}-{m}^{ref}),\end{array}$

其中:ξ为极小的正实数,其作用是确保分母不为0。

2 模型算例

2.1 模型算例1

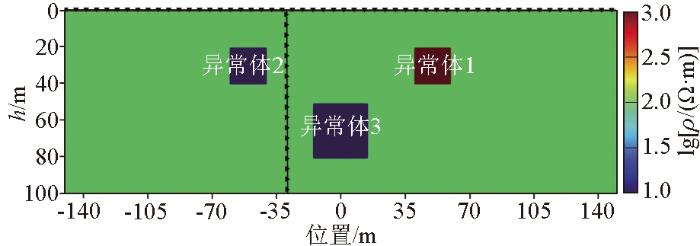
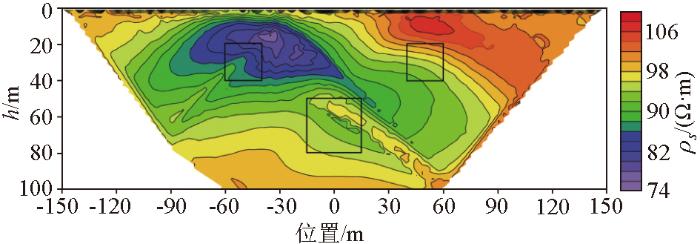
为验证算法的有效性,并比较“地—井”观测与传统地表观测方式的优劣,设计如图2所示的岩溶发育理论模型,在地下电阻率为100 Ω·m的均匀半空间中,设置3个矩形状的异常体用于模拟岩溶发育。其中,异常体1电阻率模型用于模拟不含水的岩溶,电阻率为1 000 Ω·m;异常体2与异常体3电阻率模型用于模拟含水的岩溶,电阻率为10 Ω·m;异常体1与异常体2的长、宽均为20 m,顶面埋深为20 m,异常体3的长、宽均为30 m,顶面埋深为55 m。“地—井”直流电阻率观测系统采用二极观测方式,设置地表电极150个,井中电极50个,井中电极从距离地表深度2 m处开始布置,地表与井中的电极间距均为2 m,测线的水平跨度为-150~150 m,井中电极的水平位置处于-30 m处,井中电极跨度为0~-100 m。当采用地表观测系统时,忽略井中布置的电极。基于上述参数设置进行正演计算,地表装置的正演结果如图3所示,由于“地—井”直流电阻率法的井中电极的伪剖面定义不同于地表装置,暂时无法给出“地—井”直流电阻率法的视电阻率等值线图。将得到的理论数据中加入5%的随机噪声后再进行反演。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 简单理论模型

Fig.2 Simple theoretical model

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 地表装置的视电阻率等值线

Fig.3 Apparent resistivity contour map

按照野外工作的一般经验,地表装置的观测数据的有效反演深度约为测线长度的1/6,所以一般会根据项目要求决定地表装置的测线长度。有必要对模型设置作出一定的说明,对于本文的理论模型设置而言,测线长度为300 m,则有效反演区域应为-50 m以上的倒梯形,由于这里具体讨论的是“地—井”装置有助于提高反演结果中深部异常体分辨率的有效性,所以在超出经验上的有效反演深度的区域外设置了一个低阻异常体用于论证井中电极对反演的影响,同时也能从地表装置的视电阻率等值线图中看到超过-50 m的深度后,可获得的视电阻率信息迅速减少。

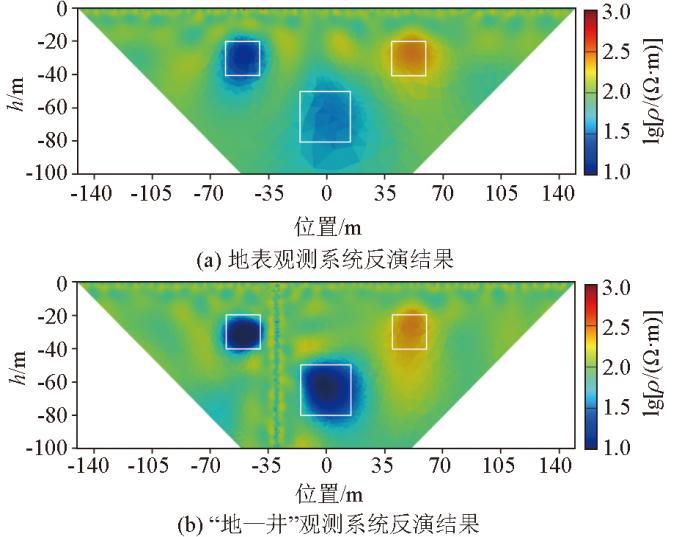
直流电阻率反演电阻率的初始模型为100 Ω·m的均匀半空间,初始正则化因子μ=1 000,反演结果如图4所示,图4为地表观测系统反演结果,图4b为“地—井”观测系统反演结果。两种观测系统的反演结果可以分为浅部和深部分别进行对比分析:对于浅部的两个异常体而言,地表装置和“地—井”装置的反演结果均能明显判断出低阻异常体与高阻异常体的空间位置和异常体轮廓,由前文可知,井中电极布置在-30 m 处,对比不同装置反演的浅部低阻异常体可以看到,有井中电极参与的反演结果,异常体的轮廓大小更接近真实模型,且浅部低阻异常体(异常体2)的物性值与真实模型更为接近;对于深部的低阻异常体而言,“地—井”观测系统反演结果中深部低阻异常体(异常体3)的位置反演得更准确、异常体轮廓更清晰以及电阻率物性值也更接近真实值,异常特征的恢复效果明显优于地表观测系统反演结果。由此可见,“地—井”直流电阻率装置有利于提高深部异常体反演的分辨率,在地表装置测线长度一定时,利用钻井布置井中电极的方式有助于获得深部电流的分布信息,扩大有效勘探区域。因为“地—井”装置无法用传统地表装置的理论去定义其视深度,以及无法确定引入井中电极后的数据覆盖范围的变化,所以,目前“地—井”装置反演结果的区域按照地表装置切图,呈倒梯形。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 反演结果对比

Fig.4 Comparison of inversion results

2.2 模型算例2

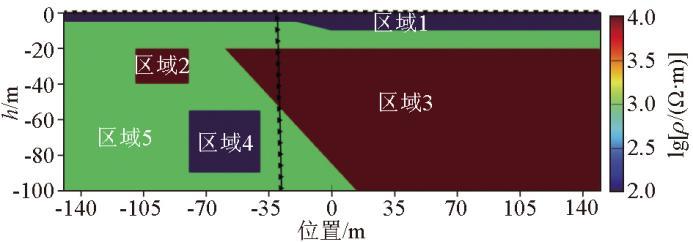
为了进一步验证“地—井”直流电阻率法的反演能力,设计了如图5所示的复杂理论模型,区域1电阻率模型模拟地表覆盖薄层黏土层,电阻率为100 Ω·m,厚度在0~10 m之间;区域2电阻率模型模拟灰岩中不含水岩溶发育区,电阻率为10 000 Ω·m,长、宽分别为30 m、20 m,顶面埋深为20 m;区域3电阻率模型模拟侵入的高阻岩层,电阻率为10 000 Ω·m,顶面埋深为20 m;区域4 电阻率模型模拟含水岩溶区,电阻率为100 Ω·m,长、宽分别为45 m、40 m,顶面埋深为55 m;区域5 电阻率模型模拟灰岩地层,电阻率为1 000 Ω·m。采用与前文理论模型相同的观测系统和反演参数设置分别进行正反演计算。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 复杂理论模型

Fig.5 Complex theoretical model

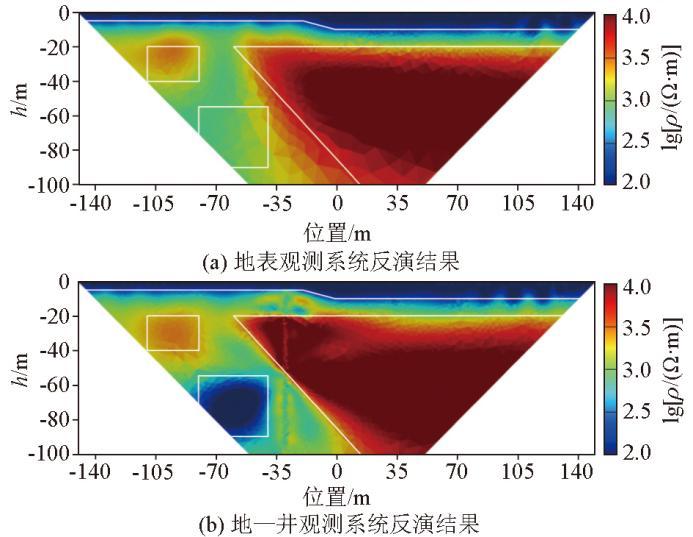
反演的初始模型是电阻率值为1 000 Ω·m的均匀半空间,初始正则化因子μ=1 000,反演结果如图6所示,图6为地表观测系统反演结果,图6b为“地—井”观测系统反演结果。对比分析图6反演结果可知,地表观测与“地—井”观测系统反演结果中区域5、区域1的浅部低阻薄层与区域3的高阻体3个区域之间的边界划分清晰,且物性值接近真实值;浅层的区域2 高阻异常(模拟不含水岩溶发育),两种观测系统反演结果接近,均能明显地判断出高阻异常的位置与规模,但是“地—井”装置反演结果的分辨率更高,轮廓形状更接近真实模型。对于深部的区域4低阻异常(模拟含水岩溶发育),由于其所处位置较深(已超出经验的有效反演深度)且靠近高阻异常(区域3),地表观测系统的电流难以抵达,分辨能力有所下降,导致地表观测反演结果的异常响应较弱,难以判断其位置及规模;相比于地表观测反演结果,“地—井”观测系统可以通过井中电极获取深部电流分布信息,从“地—井”观测方式的反演结果中可以清晰地判断深部低阻异常的位置,异常体的规模和物性值与真实模型吻合,反演效果明显优于高密度直流电地表观测系统。复杂理论模型的反演结果进一步说明,地表测线长度一定时,借助钻井布设电极的“地—井”装置能有效拓展地表装置的勘探深度,提高深部异常的相应特征及反演结果的分辨率。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 反演结果对比

Fig.6 Comparison of inversion results

3 实测数据反演

理论模型反演结果均表明:“地—井”直流电阻率方法可以有效地提高反演模型的分辨率,尤其是靠近井中电极的反演区域。为探讨该方法的实际应用效果,选取了两个路基岩溶“地—井”装置应用实例,并对其反演结果加以分析论证。

3.1 应用实例1

实例1为江西吉安某地路基岩溶勘探工程,该工作区地形平整,地表覆盖层主要为粉质黏土与中砂,覆盖层厚度约为3~10 m,基岩为灰岩,工作区内未见有出露的灰岩。“地—井”高密度电阻率法采用分布式高密度电阻率法仪器进行三极阵列测量,地表共布置电极40个,电极间距为5 m;由井底向上开始测量,每测完一次排列后将电极上移5 m再进行下一排列测量,直至电极到达地表结束测量。测线布置及钻孔位置如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 测线布置示意1

Fig.7 Schematic diagram of survey line layout 1

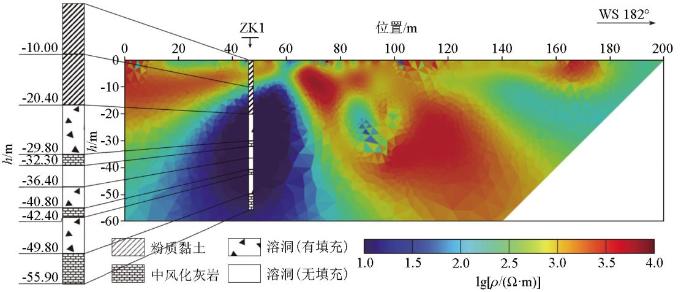
在测线47. 5 m处的验证钻孔ZK1揭示:0~20. 4 m为粉质黏土;20. 4~29. 8 m为角砾质黏土;29. 80~55. 90 m为中风化灰岩与溶洞交替出现,其中溶洞总厚度为15. 9 m。

该工作区实测数据反演结果如图8所示,图中标有钻孔柱状简图及其等比例放大示意图。结合柱状简图分析,在钻孔位置处由浅入深依次是粉质黏土(厚度20. 40 m)、溶洞(厚度9. 50 m)、中风化灰岩(厚度2. 50 m),而后则是溶洞与中风化灰岩交替出现。由于实际测线布置不同于理论模型,钻井的位置处于测线的一端,这意味着远离钻井的一侧,其深部获得的电流分布信息远不如靠近钻井的一侧,综合考虑,应用实例的反演结果呈现倒立的直角梯形状。从图8中易观察到,钻孔位置处浅部高阻对应的是粉质黏土层,而深部大区域低阻则对应中风化灰岩和溶洞,处于该部分的中风化灰岩裂隙较发育且普遍存在漏水的情况,电阻率特征呈现与岩溶电阻率值接近的低阻,因此在反演图像中呈现一整块的低阻异常,反演结果基本符合钻孔资料。在反演图像中,除钻孔位置外还有两处明显低于围岩的区域,但这两处电阻率值(约700 Ω·m)明显高于岩溶发育区域的电阻率值,初步推测这两处电阻率值低于围岩的原因是含水较多,按照经验上的有效反演深度,即使最右侧远离钻井,但仍能保证深度30 m以上区域的反演精度,故笔者确信测线最右侧低阻区域的反演结果是可信的。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 实测反演结果

Fig.8 Measured inversion results

3.2 应用实例2

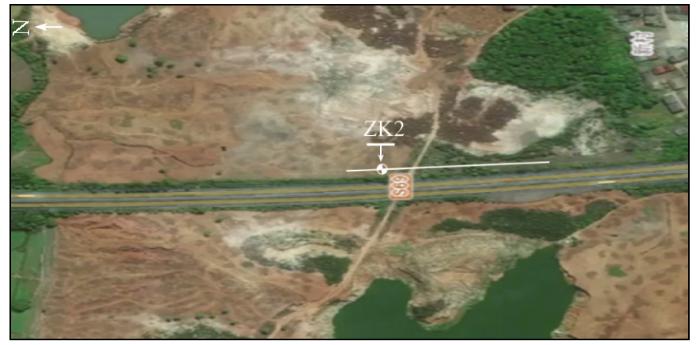
实例2所在的区域是一个低岗埠地,主要地貌类型为岗埠和山间冲积盆地,测线布置及钻孔位置如图9所示,整个区域地形略有起伏,总体呈现西高东低的趋势,但总体起伏幅度较小。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 测线布置示意2

Fig.9 Schematic diagram of survey line layout 2

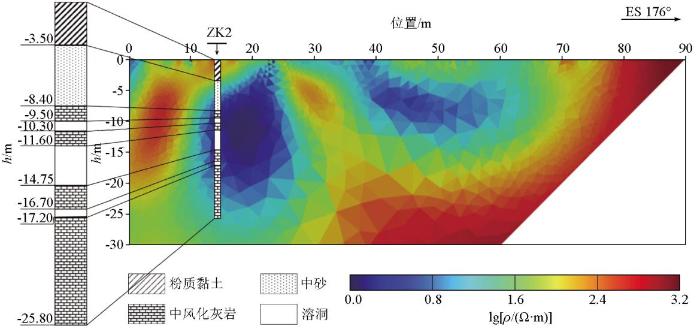
采用与应用实例1相同的测线布置方式与参数进行数据采集,并采用与应用实例1相同的反演参数设置及方法进行反演,反演结果见图10。钻孔位于测线14.5 m处,图中钻孔ZK2揭示:0~3.5 m为粉质黏土,3.5~8.4 m为中砂,8.4~25.80 m为中风化灰岩与溶洞交替出现,溶洞总厚度为4.95 m。与应用实例1情况一样,钻井处于测线的一端,故反演区域呈现倒立的直角梯形状。结合柱状简图和该实测数据反演结果可见,在钻孔位置处,深度位于-8.40~-17.20 m的低阻区域正好对应柱状图中的中风化灰岩与溶洞交替出现的区域,粉质黏土层对应高阻,中砂层对应中阻,反演结果与柱状图所示分层信息基本吻合;在反演图像中,钻孔ZK2位置右侧,深度在-5~-13 m处有电阻率值明显低于围岩的低阻异常,且电阻率值与钻孔位置处的低阻区域电阻率阻值相近,初步推测该处存在溶蚀发育。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 实测反演结果

Fig.10 Measured inversion results

4 结论

为了提高直流电法在岩溶探测的分辨率与探测深度,开展了“地—井”直流电法的研究,通过理论模型与实际应用,取得了以下几点认识:

1)“地—井”直流电法通过引入井中电极提高了深部电流分布水平,可更有效地获取深部电流分布信息,从而提高了深部的异常识别和反演分辨率。

2)该方法成功应用于江西某地路基岩溶探测的调查工作中,通过“地—井”高密度直流电法观测,更清楚地反映了地下基岩面岩溶发育情况,表明了“地—井”观测系统的优势,验证了“地—井”直流电阻率法的有效性和实用性。

3)鉴于井中电极的视电阻率断面难以获得,现研究阶段对井中电极相对于地表高密度装置所能增加的有效勘探范围仍处于定性分析的层面,将在后续的工作中,拟通过“地—井”装置的灵敏度分析进一步确定其数据覆盖范围与“地—井”数据中影响不同区域的分辨率因素。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

吴亚楠.

高密度电阻率法在莱芜市泉河地区岩溶地质勘查中的应用

[J]. 中国岩溶, 2018, 37(4):617-623.