0 引言
光泵磁力仪在灵敏度、测量精度和测量范围方面均有显著优势,被广泛应用于地球物理探测领域。按照共振元素可以分为碱金属磁力仪,如钾(39K)、铷(87Rb、85Rb)、铯(133Cs)磁力仪,以及氦(4He)、汞(Hg)、氮(N)、氢(H)等磁力仪;按照控制电路可以分为跟踪式磁力仪和自激式磁力仪。而跟踪式氦光泵磁力仪以无需加热、数字化程度高、绝对精度高等优势,被广泛应用于航空磁测、地面磁测以及海洋磁测中[1
中国自然资源航空物探遥感中心研制的氦光泵磁力仪在测量灵敏度、磁测范围等方面达到过世界先进水平,并出口美国[5],但存在着仪器体积大、重量大、功耗大、数字化程度不高等劣势[6]。此外,受中美贸易战的影响,灵敏度优于20 pT/Hz1/2的磁力仪对华禁售[7]。因此,国产数字化跟踪式磁力仪的研制过程中,需要对传感器、模拟电路、数字信号处理等各个环节展开系统性研究。其中滤波器作为磁力仪的关键器件少有专门的研究,吉林大学在磁测相关技术研究中,将滤波器作为信号检测和提取的重要环节部署在锁相放大器(lock-in amplifier,LIA)[5-6]、频率计数器以及数据采集等模块中,对磁力仪最终性能直接起到巨大的作用。
低通滤波作为LIA的关键部分,已有的研究采用动态平均模块去除交流信号,起到直流滤波器的作用,可应用于不同类型的低频光热实验中[12];在数字地震数据采集站的设计中,通过抽取滤波和补偿滤波、半带FIR(finite impulse response,有限脉冲响应)滤波再叠加IIR(infinite impulse response,无限脉冲响应)滤波器的方式,可以将512 kbps的数据降转成采样率为1 kHz的24位信号输出[13];中国科学院电子所研制的数字电离层测高仪,在信号接收端的数字下变频设计中,通过积分梳状(cascaded integrator comb,CIC)滤波、补偿滤波器和可编程滤波器的结构,降低数据速率并限制输出有效带宽,大大提高了接收机的动态范围[14]。
本文仅对LIA内的滤波器开展设计、仿真和制作,选用CIC加IIR滤波器的级联结构,消除奈奎斯特(Nyquist)采样异常,减少了硬件消耗,提高了锁相放大器的性能。
1 滤波器在跟踪式氦光泵磁力仪中的应用
1.1 氦光泵磁力仪的磁测原理及组成
其中:γ为氦原子旋磁比。
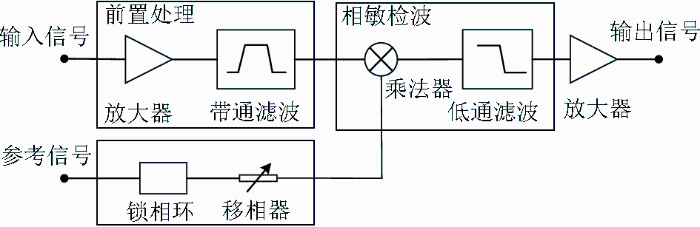
跟踪式氦光泵磁力仪主要由传感器和信号检测系统两大部分组成。传感器中的氦原子产生前述的光泵作用及磁共振作用,信号检测系统则对磁共振频率进行测量和跟踪。本文设计的跟踪式氦光泵磁力仪系统(图1)采用16 MHz的射频激励源,以保证氦灯和原子气室内的原子处于亚稳态;短暂高压激发起到启辉器的作用,以加快气体激发;信号检测系统根据传感器输出的灯室吸收光强的变化,来调节射频场的频率。整个过程通过自动增益放大、带通滤波、模数转换(analog to digital)、LIA、比例积分微分(proportional integral differential,PID)控制、直接数字频率合成(direct digital synthesizer,DDS)、数模转换(digital to analog)以及信号驱动,最终反馈到传感器,实现磁场测量的自动跟踪。本文通过设计、仿真和FPGA(field programmable gate array,现场可编辑逻辑门阵列)实现锁相放大器的关键部分——滤波器,完成对磁场的锁定和跟踪。
图1
1.2 射频信号检测
氦光泵磁力仪的信号检测系统首先需要快速变化的射频场,使光学系统中的氦原子达到磁共振状态;其次需要保持磁共振的状态,用以实现对外磁场的锁定和跟踪。在外磁场和射频场作用下,光学系统的光电信号与射频场频率形成的磁共振曲线(图2a)呈洛伦兹线形[5]。当外磁场变化较小时,射频在共振点频率f0附近变化,易于实现信号锁定和跟踪;但当磁场变化较大时,则需要重新在大范围内寻找共振点,从而导致难以准确和快速地完成磁场测量。因此,通过对调制信号的基波(共振曲线的一阶导数)和二次谐波(共振曲线的二阶导数)进行检测,可以更快速地对射频信号进行判断和跟踪。如图2b、c所示,通过判断二次谐波信号的幅值是否大于零,定位基波的线性区(f1~f2),即跟踪区;再通过基波的零值判断,获得精确的共振点f0,从而实现准确、快速的磁测功能。
图2
图2
磁共振(a)、基波(b)和二次谐波(c)曲线模型曲线对比
Fig.2
Magnetic resonance curve (a), fundamental wave (b), and second harmonic curve (c) model diagram
1.3 锁相放大器
在磁力仪的信号处理过程中,需要从电路中的低频1/f噪声、工频干扰及光电二极管噪声等干扰中提取基波信号和二次谐波信号。这就需要锁相放大器从噪声环境中提取已知频率的基频和二倍频信号。
数字LIA的核心部分由相敏检波器和低通滤波器两部分组成(图3)。LIA首先对输入信号x(t)进行放大以实现信号幅度的匹配;之后通过带通滤波器滤除部分噪声,以排除外界干扰;然后将输入信号与经过相移调整的同频参考信号r(t)相乘,以实现频谱搬移;最后对乘积信号进行低通滤波,即可得到所需的信号。
图3
上述过程中,设x(t)的幅度为Vs,频率为ω0,初始相位为ϕ0;r(t)的幅度为Vr,频率为ω0。则x(t)=Vssin(ω0t+ϕ0),r(t)=Vrsin(ω0t),根据三角公式输出y(t)为:
由式(2)可见,经过乘法器后的相敏检波信号实现了对输入信号频谱从ω0到零频和2ω0的频率迁移。这时再通过低通滤波器将高频2ω0分量滤除,就可以得到与相位有关的直流分量输出u(t)=
商品化的LIA存在体积大、功耗大、集成度低等问题,无法满足小型数字化氦光泵磁力仪的要求,因此急需开发出数字化小型LIA模块,并通过FPGA实现。这其中的关键技术之一就是设计研制合适的低通滤波器模块。
2 滤波器的选型与设计
在锁相放大器中,当输入信号x(t)中混有干扰噪声n(t)时,通过乘法器得到的相敏信号除了有直流量和二倍频分量外,还包含了x(t)和n(t)各频率的和频项与差频项。若此时噪声频率与输入信号频率相差较小,则差频分量频率较低,这就需要低通滤波器的带宽足够窄,因此,本文选择了多级CIC、IIR级联结构的滤波器,用以保证输出结果更好地抑制噪声,仅输出包含幅度和相位特征的直流分量。
2.1 CIC滤波器
在高速信号检测系统中,需要对氦光泵磁力仪的基波、二次谐波信号进行提取。由于LIA中低通滤波器的带宽需要足够窄,尽量满足只允许直流通过的要求,若此时以数字电路的AD采样率直接设计低通滤波器,则滤波器的阶数会非常高,导致占用大量FPGA和DSP(digital signal processing,数字信号处理)资源,因此需要通过多速率信号处理的方式设计滤波器,在满足奈奎斯特抽样定理,即采样频率必须大于最高频率的2倍的前提下,实现数字采样率的转换。
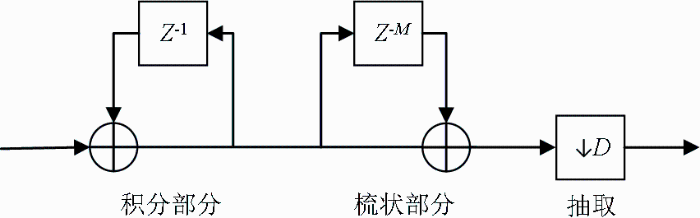
图4
积分部分和梳状部分在Z域(复数频域)中系统函数分别表示为:
其中:D是滤波器的抽取倍数,M是梳状器的阶数,二者通常是一致的,计算时DM也可以作为一个整体来表示单级CIC的延迟或抽取倍数,或仅用抽取倍数表示。整个CIC滤波器可看作系数均为1的一个IIR滤波器与一个FIR滤波器级联后再进行抽取而得到的,其系统函数H(z)可表示为:
对应不同频率ω的幅频响应为:
图5
图5
不同抽取倍数的单级CIC滤波器幅频特性
Fig.5
Amplitude frequency characteristics of single stage CIC filter with different decimation factor
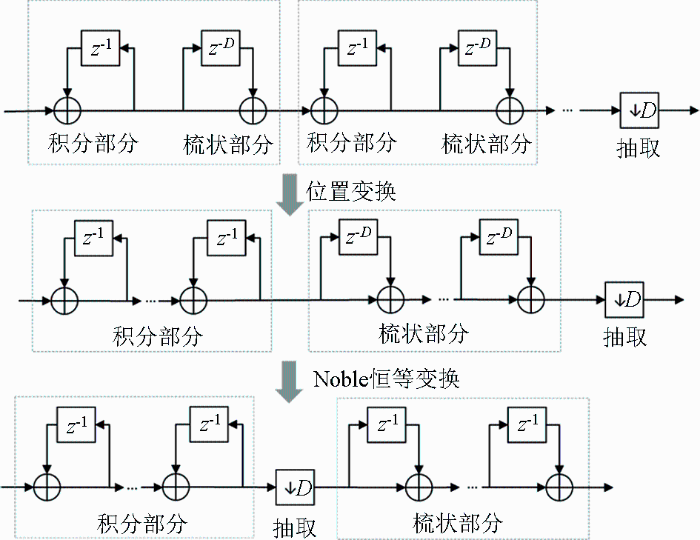
多级CIC滤波器可以通过多个单级CIC滤波器直接叠加实现,但在FPGA实现时还需考虑资源占用与运算速度问题。由式(5)可见,在进行抽取之前,单级CIC滤波器由一个D阶梳状滤波器和一个一阶积分器组成,根据Noble恒等式(7)[19],多级系统在信号处理的过程中,可以通过改变线性系统、内插、抽取的顺序,使系统实现的方式更简便,即:
因此,对于N级CIC滤波器级联(图6),通过Noble不等式可以调整积分、抽取、梳状环节的顺序,将积分部分与梳状部分分别放在一起,且将抽取放到梳状滤波器之前,就可以将梳状滤波器的阶数降为1,从而大大节约FPGA的资源,使得多级CIC滤波器更易于实现。此时,N级D抽取的CIC滤波器的系统函数为:
图6
当D=8,N分别取1~5时,CIC滤波器的幅频响应如图7所示。可以看出,4级CIC滤波器的旁瓣衰减达到了50 dB以上,主瓣衰减变大,因而设计多级CIC滤波器时N一般不超过5级。
图7
图7
相同抽取倍数的多级CIC滤波器归一化幅频特性
Fig.7
Normalized amplitude frequency characteristics of multi-stage CIC filters with same decimation factor
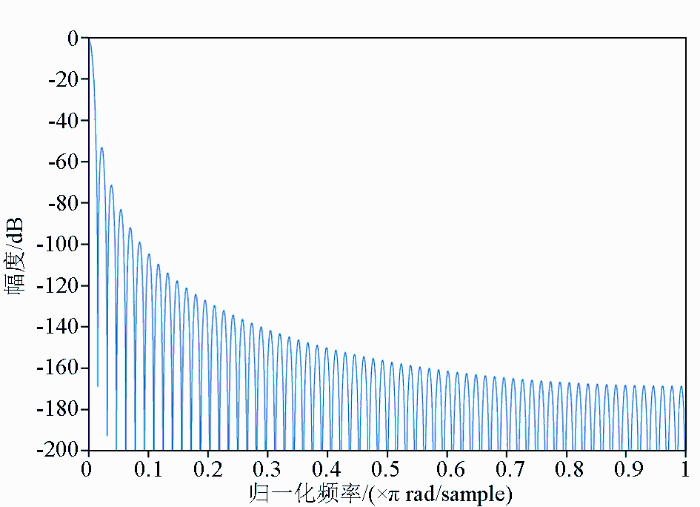
对于本文所设计的氦光泵磁力仪,数字电路的AD采样频率为200 ksps,射频场频率调制信号的基波约为1.562 5 kHz,二次谐波为3.125 kHz。为保证此频率及其高次谐波经过CIC后的衰减最大,抽取倍数取200/1.5625=128。所以,本次设计应用的CIC滤波器参数D=128、N=4时,得到的频率响应结果如图8所示。当采样频率为200 k时,对应图中第一个峰谷1.562 5 kHz处和第二个峰谷3.125 kHz处的衰减,衰减幅度均在160 dB以上,说明该CIC滤波器可以充分实现对基波及其高次谐波的滤波。
图8
图8
4级128倍抽取CIC滤波器归一化幅频特性
Fig.8
Normalized amplitude frequency characteristics of 4-stage CIC 128 times decimation filter
2.2 IIR低通滤波器
数字低通滤波器根据单位脉冲响应类型可分为有限脉冲响应和无限脉冲响应两种。与FIR滤波器相比,IIR数字滤波器在结构稳定性、线性相位特性等方面有一定劣势,但功能实现更高效,达到相同的滤波效果只需FIR阶数的1/5~1/10[20],适用本文占用更少硬件资源的需求。
IIR滤波器的系统函数为:
其中:al、bi为对应单位延迟的分母、分子系数。在实际的工程应用中,经常会直接设计一阶低通IIR滤波器(也称作惯性滤波),实现一个电阻电容(RC)低通滤波的功能。在前文的设计中,CIC滤波器已经实现降频并滤除高次谐波,因而此处需要进一步在低频段进行简单的低通滤波以获得直流分量,此处适合采用实现方式简单、节约FPGA及DSP资源且便于电路快速处理的一阶低通数字IIR滤波器[21]。此时,滤波的系统函数为:
其中:滤波系数
归一化参数
图9
图9
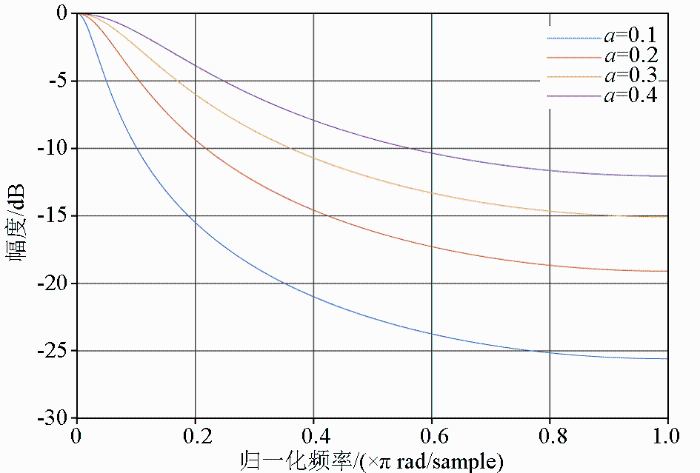
不同a取值对应一阶低通IIR滤波器的幅频特性
Fig.9
Different a values correspond to amplitude frequency characteristics of first-order low-pass IIR filters
图10
图10
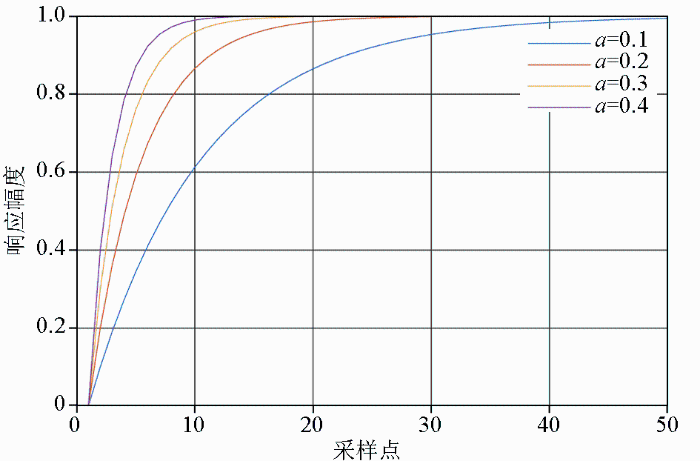
不同a取值对应一阶低通IIR滤波器的时域特性
Fig.10
Different a values correspond to time domain characteristics of first-order low-pass IIR filters
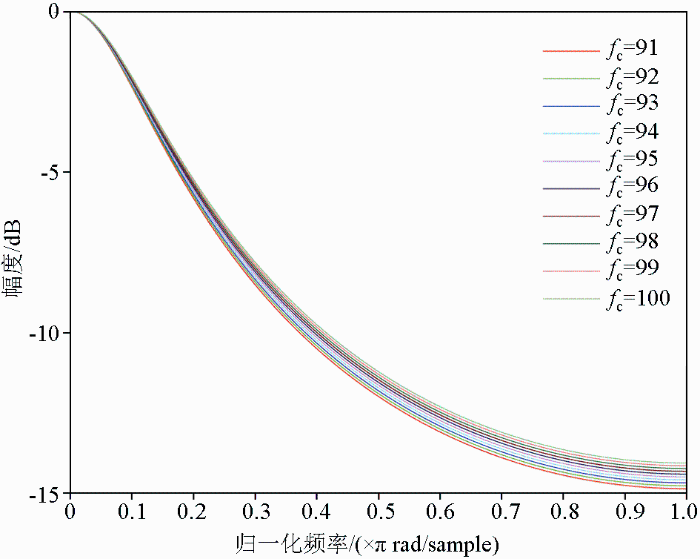
此时,根据式(11)和(12)对fc在一定范围内选取和量化,如图11所示。
图11
图11
不同fc取值对应一阶低通IIR滤波器幅频特性
Fig.11
Different fc values correspond to amplitude frequency characteristics of first-order low-pass IIR filters
当fc取值在小范围内变化时,对应低通IIR滤波器的频率响应曲线变化不大。考虑到FPGA实现过程中需要对滤波器系数进行量化的问题,选取r=fc/fs=3/1562.5=0.595 2,a=1-e-2πr≈1-e-0.373 98=0.312 006。此时对滤波参数进行8位量化的结果与计算结果接近,得到的系统函数为:
参考上文CIC滤波器使用级联的方式用于增强滤波效果,此时IIR滤波器也可以通过两个相同一阶IIR级联的方式,得到系统函数式(14),进一步增强低通滤波的效果,如图12所示。
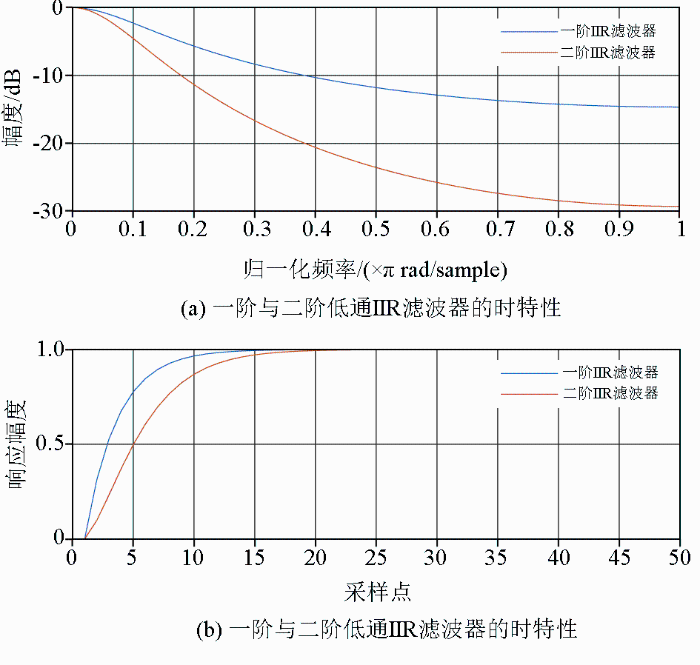
二阶IIR滤波器的响应速度略逊于一阶IIR,但幅频响应曲线的陡降更大,如图12所示。与其他一阶IIR低通滤波器相比,在满足快速响应的同时能够更好地滤除高频噪声,实现提取直流分量的效果。
图12
图12
一阶与二阶低通IIR滤波器对比
Fig.12
Comparison of first-order and second-order low-pass IIR filters
3 基于FPGA的低通滤波模块实现
3.1 低通滤波在锁相放大器中的FPGA实现
将4阶128抽CIC滤波器与二阶IIR低通滤波组合,应用到氦光泵磁力仪中,即可作为锁相放大器的低通滤波模块,用于基波信号的检测与提取,从而实现对磁场的跟踪与检测。在FPGA的实现过程中,为了减少资源占用,提高运算速度,需要在量化时将式(14)中分母的第一项量化调整为2的整数次幂[13],以移位代替除法计算。量化后的系统函数为:
FPGA代码模块化处理后如图13所示。锁相放大器模块主要由时钟、分频模块、乘法器、CIC滤波器、降采样、二阶低通IIR滤波器以及输出(22位或14位)几个部分构成。该模块的输入信号主要为时钟信号、基波信号和同频参考信号,并可根据不同精度需求选择不同位数的直流输出信号幅度。
图13
CIC的滤波器幅频响应曲线的每个旁瓣都是固定宽度,与抽取倍数相关。因此在二次谐波信号的检测中也可以使用相同的结构,如图14所示。
图14
图14
用于二次谐波信号提取的锁相放大器
Fig.14
Lock-in amplifier for second harmonic signal extraction
基波选取的线性区较小,也即共振点附近范围较小,此时磁场测量的精度较高,但这也意味着磁场发生剧烈变化时,易发生信号丢失的现象,即失锁;反之,二次谐波幅值选取较小时,当外磁场大范围变化时,调频信号不需要大范围重新扫频来实现信号跟踪,即可快速跟踪磁场变化,但此时的磁测精度较低。因此需要在二次谐波信号低通滤波输出之后增加一个幅值判断模块,以便后续进行PID控制,平衡氦光泵磁力仪的灵敏度和稳定性。
3.2 二次谐波信号输出结果
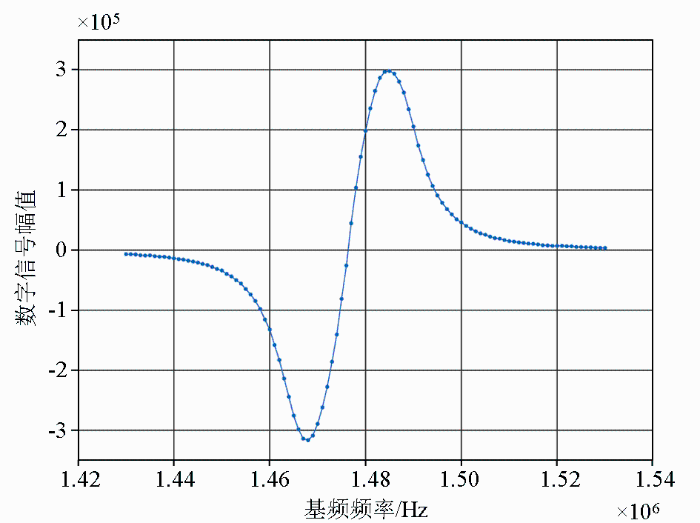
为了获得更好的结果,在屏蔽筒内一定范围内按照一定的步长进行扫频,输出二次谐波实测信号波形(图15)。当屏蔽筒内磁场设定为52 000 nT时,在该磁场范围附近扫频进行磁测,频率范围为1.43~1.53 MHz,对应磁场范围约为50 000~54 000 nT;纵坐标表示AD转换及滤波之后数字信号的幅值。
图15
由此可见,经过低通滤波后的二次谐波的实测波形基本符合理想波形。二次谐波的幅值在共振区不为零;当幅值大于零时,对应基波信号在线性区,即射频信号在跟踪区,当二次谐波达到峰值时,即为共振点,对应的射频频率为1.477 MHz;此时通对二次谐波峰值附近的幅值判断,即可由扫频转换为PID控制,从而再通过基波信号检测实现共振点的准确跟踪。
3.3 基波信号输出结果
通过二次谐波的幅值判断,信号检测系统即进入到磁共振区内。此时需要判断基波信号的幅值是否为零,以实现在共振区中精确搜索磁共振点(图16)。
图16
经过低通滤波后基波的实测波形基本符合理想的洛伦兹曲线一阶导数波形。在共振区内时,基波的幅值近似线性变化,谷值和峰值分别对应共振曲线斜率最小和最大处,两点之间即为线性区,也是磁力仪的跟踪区。在跟踪区内,基波幅值由负变正,在零值时对应共振点,因而此时可以直接通过PID控制滤波后的基波幅值,实现对磁场的锁定和跟踪,并最终获得被测磁场值。
3.4 锁相放大器模块关键指标
由本文的低通滤波环节所形成的锁相放大器能够提取噪声环境中的有用信号,还可以根据实际的磁测需求调整或添加相应功能,如输入模式、通讯接口、灵敏度等。根据表1中的对比可见,与市场上成熟的锁相放大器产品相比,基于本文所设计的低通滤波环节的锁相放大器在功能方面与商品化的锁相放大器相差不大。但市场同类相关产品多是具备一定功能的测量仪器或是模块,通常具有一定体积和较大的功耗,不能高效地嵌入于氦光泵磁力仪或其他航空物探仪器当中。因此,作为可移植的嵌入式FPGA模块,本文设计实现的锁相放大器在功耗和体积方面大大优于以上几种成熟产品,不仅可以根据实际应用,实现提取一定频率范围内的频率信号的功能,还可以降低整个氦光泵磁力仪系统的功耗,便于开发出小型化、便携化的新一代航空磁场测量仪器。
表1 本文设计的数字锁相放大器与市场相关产品的关键指标对比
Table 1
| 参数 | 斯坦福SR830锁相放大器 | OE1300锁相放大器模块 | 苏黎世MFLI锁相放大器 | 本文设计锁相放大器 |
|---|---|---|---|---|
| 输入模式 | 单端/差分电压输入 电流输入 | 单端/差分电压输入 电流输入 | 单端/差分电压输入 电流输入 | 单端/差分电压输入 电流输入 |
| 满量程灵敏度 | 2nV~1V | 1nV~5V | 1nV~3V | 1nV~5V |
| 电源电压 | 100、120、220、240VAC | 12VDC±5% | 12VDC 100~240VAC,50/60Hz | 9~36VDC |
| 功率 | 40W | 18W,不超过242 | <40W | 5~6W |
| 通讯接口 | GPIB、RS232 | UART、网口 | LAN、USB | UART、网口等可选 |
| 尺寸 | 495.3cm×43.18cm× 13.34cm | 裸机181.3mm×100mm×43.8mm 机壳204mm×110mm×46.8mm | 28.3cm×23.2cm×10.2cm | 可内嵌于 10cm×10cm×10cm机壳内 |
4 氦光泵磁力仪磁场测量输出结果
本次设计的数字化氦光泵磁力仪工作时,首先在大范围内以一定的步长扫频,通过二次谐波的幅值判断进入跟踪区之后,再通过基波是否为零判断信号是否在共振点。找到共振点后,直接通过PID控制滤波后的二次谐波和基波的幅值,磁力仪即可达到稳定的磁测状态,实现对磁场的锁定和跟踪,输出被测磁场的大小。
4.1 磁场信号
图17
图17
将氦光泵磁力仪置于屏蔽筒内进行测试
Fig.17
Optically pumped helium magnetometer tested in a shielded cylinder
图18
图18
氦光泵磁力仪进行连续测量结果
Fig.18
Continuous measurement results of optically pumped helium magnetometer
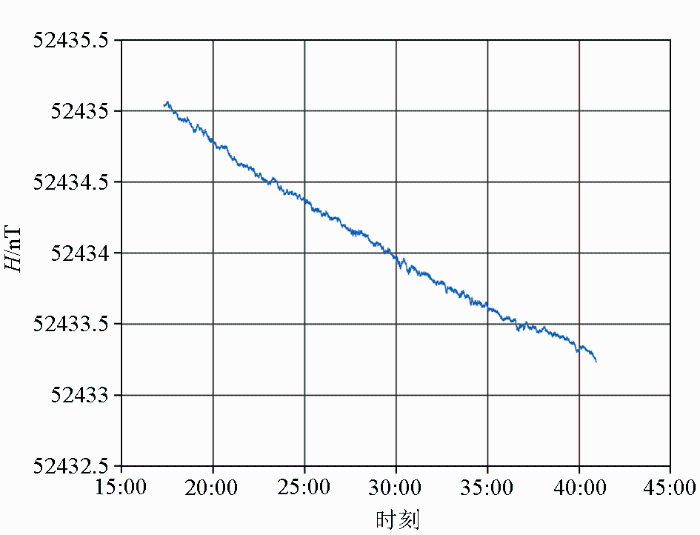
图18横坐标为时间,表示一定时间内以10 Hz频率对磁力仪输出进行数据采样;纵坐标为氦光泵磁力仪最终输出的磁场值。记录的数据约为23 min内磁力仪在屏蔽筒内的测量结果,测量期间尽可能地屏蔽外磁场的扰动,获得的磁场均值约为52 434.07 nT。测试结果说明该段时间内磁力仪可以实现对地磁场的跟踪测量。
4.2 PSD信号
图19
4.3 四阶差分静态噪声
根据《航空磁测技术规范》[23],航空磁力仪的静态噪声水平Sn可用连续观测值的均方根表示:
其中:n表示参与计算的点数;
表示第i个元素的四阶差分,T 表示磁场值;
表示n个四阶差分值B'i 的平均值[24]。
经计算,运用本次设计的锁相放大器的磁力仪,该段时间内的静态四阶差分测试结果为1.729 pT,满足航磁规范中磁力仪静态噪声水平的一级要求(Sn≤0.01nT),说明氦光泵磁力仪稳定性良好,满足《航空磁测技术规范》的技术指标要求。
4.4 磁场动态测量
根据《航空磁测技术规范》要求,航空磁力仪的带宽需要≥0.5 Hz(或阶跃响应上升时间≤1 s)。通过实验室测试,在屏蔽桶内的磁力仪,当外加磁场快速改变时(图20),通过加载本文设计的低通滤波模块的锁相放大器,磁力仪可以实现对变化的磁场值跟踪,磁力仪的阶跃响应迅速,在0.2 s以内磁力仪即可根据磁场的变化快速响应,符合航磁规范要求。
图20
图20
氦光泵磁力仪的动态测试结果
Fig.20
Dynamic test results of optically pumped helium magnetometer
5 结论
本文设计的数字低通滤波模块,采用多级CIC滤波器与二阶IIR滤波器级联的方式,可以准确获取基波和二次谐波信号,以实现磁场的跟踪和测量。本设计具有以下特点:
1)通过CIC抽取和IIR低通滤波的方式进行模块设计,使用方便、操作简单,还可以大大减少FPGA资源使用量;所构成的锁相放大器具有体积小、功耗小等特点,有利于地球物理探测仪器的小型化发展。
2)本文设计的数字低通滤波模块,在稳定性和灵敏度等方面可以很好地满足跟踪式氦光泵磁力仪的磁测需求。
3)本文设计的数字低通滤波模块可以根据未来不同的设计需求,应用在航空地球物理探测的其他领域中,实现不同信号的检测与提取等功能。
此外,基于FPGA的硬件开发的经验和发展方向,本文设计的数字低通滤波模块和锁相放大器,还可以有进一步的发展和提高:
1)可以将锁相放大器模块的IP核成品化,便于移植到不同应用系统内。
2)可以进行仪器封装,制作商品化锁相放大器。
3)增加上位机控制软件,灵活配置滤波器的参数,适应不同的应用场景。
参考文献
Optically pumped magnetometers:From quantum origins to multi-channel magnetoencephalography
[J].
光泵原子磁力仪技术
[J].
Techniques in optically-pumped atomic magnetometer
[J].
Recent progress in optically pumped magnetometers
[J].
基于铯光泵磁力仪的地震地磁矢量测量系统
[J].
Seismic geomagnetic vector measurement system based on optically pumped cesium magnetometer
[J].
Code of Federal Regulation,Title 15,Subtitle B,Supplement No.1 to Part 774
[EB/OL].(
数字锁相放大器的算法设计与优化
[J].
Algorithm design and optimization of digital phase locked amplifier
[J].
数字锁相放大器技术及光谱检测应用进展
[J].
Progress in digital lock -In amplifier technology and spectral detection applications
[J].
FPGA-based digital lock-in amplifier with high-precision automatic frequency tracking
[J].
A Digital lock-in amplifier based on adaptive kalman filter for rail defect detection
[J].
Dual-phase lock-in amplifier based on FPGA for low-frequencies experiments
[J].
Development of a new seismic-data acquisition station based on system-on-a-programmable-chip technology
[J].
The new CAS-DIS digital ionosonde
[J].
氦光泵磁力仪探头设计和环路数字化研究
[J].
DOI:10.6038/cjg2019M0503
[本文引用: 1]

磁法勘探是一种常用的地球物理勘探方法,其中光泵磁力仪是国内外应用于航空和地面磁法测量最多的磁力仪器.为满足深部矿产资源勘查对高精度磁测设备的需求,本文开展了低噪声、宽量程的高性能数字氦光泵磁力仪关键技术研究,主要包括磁传感器探头优化设计和新型数字化环路设计两方面.首先通过深入分析影响氦光泵磁力仪灵敏度的主要决定因素,对磁传感器关键部件氦灯、氦室进行小型化技术研究,解决高性能氦泵源和原子气室等关键件的制作工艺,提高氦灯效率和氦吸收室的磁共振信号输出强度,制作出高性能、低噪声的小型化氦光泵探头.然后,针对常规模拟跟踪环路的局限性,通过数字化技术研究,采用FPGA、DSP、DDS、环路跟踪算法和信号处理软件等技术构成新型数字环路,弥补现有基于模拟跟踪环路技术的模拟式氦光泵磁力仪的不足,该数字环路降低了氦光泵磁力仪的电路噪声,增强了抗电磁干扰能力,并扩展了磁力仪的量程.本文通过小型探头和数字环路的技术设计,研制出高精度大量程的地面数字氦光泵磁力仪,并用于第三方测试.通过第三方测试证明:实测仪器的静态噪声小于4 pT,磁场测量范围为20000~100000 nT,梯度容限大于10000 nT/m.
Design of helium optical-pumping magnetometer probe and digital loop electronics circuit
[J].
光泵磁力仪频率信号高精度测定技术实现
[J].
Realization of high-precision measurement technology for frequency signal of optically pumped magnetometer
[J].
Integrated optically pumped magnetometer for measurements within earth's magnetic field
[J].
Fast digital filter for frequency discriminator
[C]//
原子磁力仪灵敏度标定方法研究
[J].
Study on the sensitivity calibration method of atomic magnetometer
[J].