E-mail Alert Rss
 

物探与化探, 2024, 48(5): 1199-1207 doi: 10.11720/wtyht.2024.1005

“短偏移距瞬变电磁法技术与应用”专栏(特约专栏主编:薛国强)

基于监督下降法的短偏移距瞬变电磁快速反演研究

饶丽婷,1,2,3,4, 武欣,2,3,4, 郭睿5, 党博1, 党瑞荣1

1.西安石油大学 电子工程学院,陕西 西安 710065

2.中国科学院矿产资源研究重点实验室 中国科学院地质与地球物理研究所,北京 100029

3.中国科学院大学 地球与行星科学学院,北京 100049

4.中国科学院 地球科学研究院,北京 100029

5.清华大学 电子工程系,北京 100084

Fast inversion of short-offset transient electromagnetic (SOTEM) data based on the supervised descent method

RAO Li-Ting,1,2,3,4, WU Xin,2,3,4, GUO Rui5, DANG Bo1, DANG Rui-Rong1

1. School of Electronic Engineering, Xi’an Shiyou University, Xi’an 710065, China

2. Key Laboratory of Mineral Resources, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China

3. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

4. Innovation Academy of Earth Science, Chinese Academy of Sciences, Beijing 100029, China

5. Department of Electronic Engineering, Tsinghua University, Beijing 100084, China

通讯作者: 武欣(1982-),男,副研究员,博士,主要从事面向地形复杂地区的矿产、地下水等资源及地下人工目标的地球物理探测理论方法研究与装备研发工作。Email:wu_xin18@163.com

第一作者: 饶丽婷(1989-),女,副教授,博士,主要从事电磁法正反演理论与数据处理方法研究工作。Email:ltrao@xsyu.edu.cn

责任编辑: 沈效群

收稿日期: 2023-01-3   修回日期: 2023-08-4  

基金资助: 国家自然科学基金项目(42004064)
国家自然科学基金项目(42074121)
河南省豫地科技集团2024年重点科研项目(JTZDKY202405)
中央引导地方科技发展资金项目(2023ZY0036)
广西壮族自治区重点研发计划项目(2023AB260490)

Received: 2023-01-3   Revised: 2023-08-4  

摘要

短偏移距瞬变电磁法(简称SOTEM)通常采用传统式基于物理建模的反演方法,反演效率较低,不易灵活融入先验信息,而基于数据驱动的反演方法能够提高反演精度与效率,泛化能力却难以保证。为了提高SOTEM数据反演的精度和效率,并兼顾可靠的泛化能力,本文探索了一种融合物理建模与数据驱动的反演方法,将机器学习中监督下降法应用于SOTEM数据反演中。基于监督下降法的SOTEM数据反演分为线下训练和线上预测,线下训练时通过合理的训练集灵活融入先验信息,获得隐含模型特征的平均下降方向,线上预测时借助物理建模函数和训练所得下降方向,在传统反演框架下完成模型参数重建。文中利用层状大地模型构建训练集和测试集,实现了基于监督下降法的SOTEM数据一维反演,并与传统Occam算法进行了对比。 结果表明:基于监督下降法的SOTEM反演效率大幅提升,反演精度较高,具有良好的泛化能力。

关键词： 瞬变电磁法; SOTEM; 快速反演; 监督下降法; 机器学习

Abstract

The short-offset transient electromagnetic (SOTEM) data are typically processed using conventional inversion methods based on physical modeling, manifesting relatively low efficiency and difficulty in integrating priori information. In contrast, the data-driven inversion methods can enhance the inversion accuracy and efficiency but fail to ensure the generalization capability. To achieve high inversion accuracy and efficiency for SOTEM data and a reliable generalization capability, this study proposed an inversion method that integrates physical modeling with the data-driven approach, introducing the supervised descent method in machine learning into SOTEM data inversion. The proposed inversion method involves the offline training and online prediction stages. In the offline training stage, the prior information is flexibly integrated into the model training through a reasonable training dataset to obtain the average descent directions with implicit model features. In the online prediction stage, the physical modeling functions and the descent directions are employed to reconstruct the model parameters under the conventional inversion framework. In this study, the layered geodetic model was applied to design the training and test datasets for the 1D inversion of SOTEM data based on the supervised descent method. The inversion results were compared with those obtained using Occam's inversion algorithm, demonstrating that the proposed inversion method shows significantly enhanced inversion efficiency, higher inversion accuracy, and higher generalization capability.

Keywords： transient electromagnetic (TEM) method; short-offset transient electromagnetic (SOTEM) method; fast inversion; supervised descent method; machine learning

PDF (4168KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

饶丽婷, 武欣, 郭睿, 党博, 党瑞荣. 基于监督下降法的短偏移距瞬变电磁快速反演研究[J]. 物探与化探, 2024, 48(5): 1199-1207 doi:10.11720/wtyht.2024.1005

RAO Li-Ting, WU Xin, GUO Rui, DANG Bo, DANG Rui-Rong. Fast inversion of short-offset transient electromagnetic (SOTEM) data based on the supervised descent method[J]. Geophysical and Geochemical Exploration, 2024, 48(5): 1199-1207 doi:10.11720/wtyht.2024.1005

0 引言

我国浅部资源逐渐消耗殆尽,开展深部矿产和油气资源探测已成为当前地球物理科学研究的重要发展方向[1]。短偏移距瞬变电磁法(short-offset transient electromagnetic method,简称SOTEM)是近几年快速发展的大深度人工源电磁探测新技术,具有信号能量强、带宽大、探测精度高等优点,已成为精细探测深部资源的有效手段[2⇓⇓⇓⇓⇓-8]。SOTEM利用接地电性源发射装置、近源观测方式提升了探测深度和精度,也为其正反演增加了难度与挑战[9⇓-11]。相比常规瞬变电磁法,SOTEM的电磁场理论更为复杂,其正演和雅可比矩阵计算更加复杂与耗时,而且SOTEM大范围观测时数据量也较多。因此,采用传统反演方法的SOTEM数据反演面临资源、效率的制约,尤其是涉及二维、三维反演难以实用化,使得SOTEM的精细探测理论优势难以有效发挥。

目前,SOTEM数据反演通常采用传统确定性反演方法[12-13],即以物理建模(正演)为基础,利用观测数据和模型约束构建目标函数,通过迭代优化获得反演结果,可归类为“基于物理建模的反演方法”。此类反演方法利用正演隐含的物理规律约束了模型参数重建过程,一般从初始值出发,通过目标函数的导数信息搜索模型更新方向,因此许多研究工作都围绕选择模型约束和优化方法展开[14⇓⇓⇓-18]。然而,由于导数中仅包含目标函数的局部信息,优化过程易陷入局部极小值中;此外,融入先验信息的方式不够灵活,许多先验信息本身也无法被简单的模型约束函数所描述;第三,迭代中需要反复求解雅可比矩阵,导致反演效率较低。由此可见,如何提升SOTEM反演过程的准确性、可靠性和高效性,成为亟待解决的关键问题。随着人工智能的兴起,机器学习技术逐渐应用于反演成像中[19⇓⇓⇓⇓-24],采用机器学习手段,建立大数据集,挖掘从数据到模型参数之间映射关系,可称为“基于数据驱动的反演方法”。此类反演方法通过大数据训练集灵活融入先验信息,在线上预测时能够加速反演过程,从而提高反演的精度和效率。然而,实际情况下训练和预测的模型空间很难保证一致,完全基于数据驱动的反演方法适用性较差,泛化能力难以保证。综上可见,模型驱动与数据驱动的反演过程之间存在较强的互补性。对两者优势结合,将有望提高反演的精度和效率,并使反演算法具有较高的泛化能力。近几年学者们开始研究“融合物理建模与数据驱动的反演方法”[25⇓⇓⇓⇓⇓-31],该方法可细分为3类:①先用传统反演算子预处理数据产生初始模型,后使用神经网络建立模型空间内的映射,提高成像质量;②先利用机器学习先验信息,后在传统反演框架下完成模型重建;③将物理算符融入神经网络,训练基于物理规律的反演成像网络。这些前沿工作为SOTEM数据反演提供了重要的参考价值。

本文引入机器学习中的监督下降法,探索了一种融合物理建模与数据驱动的SOTEM反演方法,以提高SOTEM数据反演的精度和效率,并兼顾可靠的泛化能力。监督下降法(supervised descent method,简称SDM)最早在2013年提出[32],用于求解计算机视觉中的优化问题。监督下降法分为线下训练和线上预测,属于融合式反演方法的第二类,即利用线下训练学习灵活融入先验信息,获得隐含模型特征的平均下降方向,线上预测借助物理建模函数和训练所得下降方向,在传统反演框架下完成模型参数重建。由于基于监督下降法的SOTEM数据反演融合了物理建模与数据驱动,因此,文中在方法原理中首先介绍了基于层状大地的SOTEM正演过程,随后,从传统反演方法出发,阐述了监督下降法的线下训练和线上预测过程,并给出了线下训练集设计方案。通过数值算例验证了利用监督下降法进行SOTEM反演的可行性,与传统Occam算法进行对比,表明了监督下降法的反演精度更高、效率更快,具有较好的泛化能力。

1 方法原理

1.1 正演问题

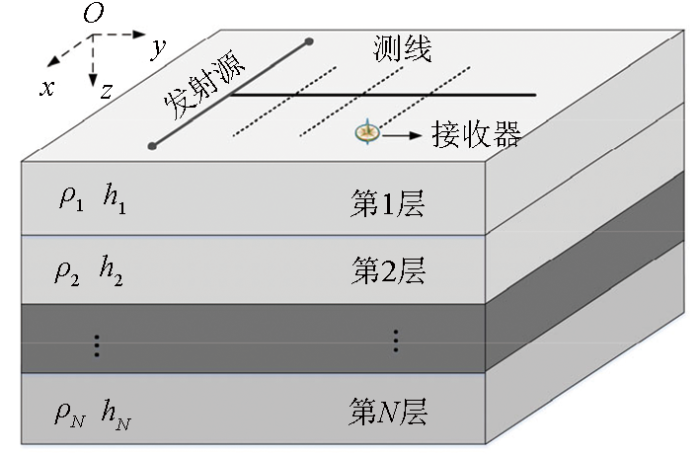
根据SOTEM实际观测情况,本文正演仅对垂直磁场进行讨论。SOTEM采用接地电性源,属于近源观测方法,发射源不能简化为单个电偶极源,而是分解为多个电偶极源,通过线性叠加各电偶极源的响应获得整个线源的电磁场响应。如图1所示,在一维层状大地模型上,水平面与xy平面重合,z轴向下为正方向,假定接地线源沿x轴铺设,总长度为S,其中心点位于坐标原点,观测点坐标为(x,y,z),接地线源产生的频域垂直磁场可分解为

Hz=∑m=1MHzdipole(ΔSm,Rm)

式中:M为分解的电偶极子数量;ΔSm为第m个电偶极子的长度;Rm为第m个电偶极子中心点到观测点在xy平面上的投影距离。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   层状大地模型上SOTEM观测示意

Fig.1   The SOTEM system configuration over the layered earth model


第m个电偶极子产生的频域垂直磁场[33]可以通过下式计算:

Hzdipole(ΔSm,Rm)=　　IΔSm4π·yRm∫0∞(1+rTE)eu0zλ2u0J1(λRm)dλ

式中:I为发射电流大小;J1为一阶贝塞尔函数,rTE为TE模式下的反射系数;rTE=λ-u^1λ+u^1。

对于N层大地,有递推公式:

u^n=un·u^n+1+untanh(unhn)un+u^n+1tanh(unhn)
u^N=uN

在准静态近似下,un=λ2+iωμσn。其中λ=kx2+ky2;ω为角频率;σn=1/ρn;ρn和hn分别为第n层的电阻率和厚度;μ为真空中磁导率。从最底层开始逐步向上递推可得到u^1。

通过数字滤波系数法计算如式(2)的汉克尔积分,可得到频率域响应[34],然后利用傅里叶变换或拉普拉斯变换获得时间域响应hz(t)或dhz(t)/dt[35]。上述正演过程可简化表示为

d=F(m)

式中:F(·)表示正演算子,其时间域响应为数据矢量d=[d1,d2,…,dK]T;dk为第k个时间窗口的响应幅度;地电模型参数为模型矢量m=[m1,m2,…,mN]T;mn为第n层电阻率。

1.2 反演问题

本研究采用机器学习中监督下降法实现SOTEM数据反演。监督下降法分为线下训练和线上预测,通过数据残差计算将物理建模融入监督下降法。线下训练时,通过数据集获得模型更新的平均下降方向;线上预测时,利用观测数据和平均下降方向,并融合物理建模过程,实现模型参数反演。其优势在于,线下训练时灵活融入先验信息,以提高反演精度,线上预测时避免雅可比矩阵计算,又利用物理建模约束模型反演过程,以提高反演效率并保证较为可靠的泛化能力。

为了更好地说明基于监督下降法的SOTEM反演原理,引入传统反演方法以作对比。在传统反演中,反演目标函数的数据残差项为

Φ(m)=F(m)-dobs2

在m=m0+Δm处作一阶泰勒展开,上式可近似为

Φ(m)=F(m0)+J0Δm-dobs2

式中:J0为正演函数在m0处雅可比矩阵。上式的最小化问题可采用高斯-牛顿法求解,获得模型更新表达式:

Δm=(JT0J0)-1JT0(dobs-F(m0))=KΔd

式中:K=(JT0J0)-1JT0,Δd=dobs-F(m0)。因此,可将式(7)最小化问题转换为已知m0时,求解如下最小二乘问题:

Φ(m)=Δm-KΔd2 。

在每次迭代中,获得K需要通过计算m0处雅可比矩阵J0,雅可比矩阵计算复杂且耗时,占据了反演大部分时间,并且K只包含了目标函数的局部信息。

在监督下降法的线下训练阶段,假设先验信息充足,使待反演模型可由L个先验模型miprior(i=1,2,…,L)线性表示,并由此可得L个仿真数据dpriori,此时,从数据空间到模型空间的线性映射K~可通过最小化如下目标函数得到:

Φ(K~)=∑i=1LΔmpriori-K~Δdpriori2 ;
Δmpriori=miprior-m0,Δdpriori=F(mpriori)-F(m0)。

式(10)为监督下降法进行线下训练的目标函数,映射K~代表了从初始模型到向真实模型更新的平均下降方向。假设在线下训练阶段,经过多次最优二乘法迭代优化,目标函数达到足够小,获得了一系列平均下降方向的映射矩阵K~j(j=1,2,…,J),第j+1步映射矩阵K~j+1的求解公式为

K~j+1=(ΔDTjΔDj)-1·(ΔDTjΔMj)

式中:ΔM、ΔD分别表示由L个样本Δmprior和Δdprior构成的模型残差矩阵和数据残差矩阵。在实际计算中,数据残差随着迭代下降很快,几步迭代后ΔDj将变成奇异矩阵。为了稳定求解过程,引入奇异值分解(SVD)和正则化参数μ,假设有ΔDj=UΣVT,式(11)转化为

K~j+1=V(Σ2+αjI)-1ΣTUTΔMj 。

在监督下降法的线上预测阶段,直接将数据残差和记录的K~j代入模型更新方程中:

mj+1=mj+K~j(dobs-F(mj)) 。

以上为线下训练和线上预测的主要过程,其实施程序步骤总结见表1。

表1   算法的实施程序步骤

Table 1  Implementation steps of the algorithm

线下训练线上预测
1)生成L个先验模型mpriori及其仿真数据diprior(i=1,2,…,L),重新排列
形成先验模型矩阵Mprior和先验数据矩阵Dprior;
2)设定M0为初始模型;
3) for j=1,2,…,J
4) ΔMj=Mprior-Mj;
5) ΔDj=F(MJ)-Dprior;
6) ΔDj=UΣVT;
7) K~j=V(Σ2+αjI)-1ΣTUTΔMj;
8) Mj=Mj+ΔDj·K~j;
9) end		1)设定m0为固定初始模型;
2) Δd=F(m0)-dobs;
3) for j=1,2,…,J
4) mj=mj+K~j(dobs-F(mj));
5) 计算当前数据拟合差rms;
6) if rms<rms0
7) 迭代终止;
8) Δd=F(mj)-dobs;
9) end

新窗口打开| 下载CSV


在实施中,为稳定求解和消除伪影,也可对线上预测的更新式进行正则化改进,同时,也可调整训练的迭代步数和预测过程以提高效率。

1.3 训练集设计

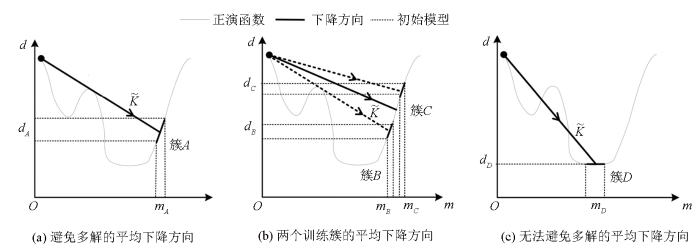
根据前文,平均下降方向K~代表了数据空间到模型空间的线性映射,在线下训练阶段,监督下降法将根据训练样本,从初始模型到向真实模型逐步更新,计算获得一系列下降方向。训练样本的特征可压缩地表示在学习的平均下降方向中,并进一步用于线上预测。因此,通过生成特定模式的训练样本集将先验信息融入反演中,用不同样本表述的先验信息能够突破数学表达式的限制,具备较高的灵活性。合理设计的训练集使训练集在样本数量适中的情况下隐含更多不同的特征,从而提高线上预测的准确性,不合理的训练集会导致错误的预测结果;同时,由于训练阶段占用大量内存和计算时间,不合理的训练集会浪费大量资源。

首先,将模型参数在一定范围内的训练集称为“训练簇”。为了说明平均下降方向与训练簇的关联性,参考图2(横轴为模型空间,纵轴为数据空间),监督下降法在第一步下降过程中,不同训练簇将获得不同的下降方向。如图2a所示,在强先验信息条件下,如可通过其他资料或解释人员的经验获得较准确的先验信息,可以构建模型参数变化范围较小的一个训练簇A,此时训练的平均下降方向K~从初始模型指向簇A内邻域。弱先验信息条件下,无法仅用一个簇来描述先验知识,训练集应包含几个最可能的簇,如图2b中,训练的平均下降方向K~位于簇B和簇C的下降方向之间,方向取决于不同簇的相对大小,各类先验信息通过调整不同训练簇的尺寸融入反演中。监督下降法并没有使用仅含目标函数局部信息的一阶或二阶导数,训练获得的下降方向能够使优化跳过局部极小值,如图2a所示。此外,需要注意的是,若训练集中不同模型生成了相似数据,监督下降法也会出现多解情况,如图2c所示,数据对簇D中模型不敏感,所有模型具有相同水平数据残差,其线上预测结果将在簇D中选择一个同时满足先验和数据残差的模型,但无法保证预测结果为准确反演解。进一步降低多解性则需要在训练阶段融入更多的先验信息。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   不同训练集的下降方向示意

Fig.2   Diagram of descent directions for different training sets


以一维地电模型为例,说明训练集的设计方法。如表2所示,根据已知先验信息(地质调查或钻孔资料等),给出各层电阻率和厚度范围,训练集中样本的电阻率、厚度参数在给定范围内随机选取,训练集的样本数量应足够多,保证样本在给定参数范围内充分遍历。若已知地电结构大致为三层模型,属于强先验信息情况,则只需包含三层模型作为训练集;若无法确定地电结构大致为几层模型时,属于弱先验信息情况,则尽可能包含三层、四层、五层模型样本作为训练集,使泛化能力更强。

表2   不同地电模型的训练集参数

Table 2  Training sets of different geoelectric models

参数三层模型四层模型五层模型
ρ1/(Ω·m)100~30080~120100~400
ρ2/(Ω·m)20~100300~50020~80
ρ3/(Ω·m)200~50050~150200~400
ρ4/(Ω·m)300~50020~80
ρ5/(Ω·m)300~500
h1/m80~20080~15050~100
h2/m100~30080~15050~100
h3/m9999150~300100~200
h4/m9999150~300
h5/m9999
个数102410241024

新窗口打开| 下载CSV


2 数值案例

本节利用数值算例验证利用监督下降法进行SOTEM反演的可行性。SOTEM系统参数设置如下:线源长度1 000 m,其中心点位于坐标原点,发射电流10 A,使用理想负阶跃电流波形激励,从10-5s到10-2s按对数等间隔分布取31个观测时间窗口,接收点坐标为(0,400,20)m,即接收点距离地表高度20 m。反演中对地下空间采用非均匀分层参数,共30层,第一层厚度为15 m,其余层厚度随着层数增加按照比例1.05逐渐增长,待反演参数为各层电阻率。由于瞬变电磁响应幅值和地电参数变化范围较大,为保证电阻率恒为正值,训练和预测过程中将数据和模型参数均转换到log10域中。硬件平台为小型工作站,处理器为AMD Ryzen 9 5950X,内存128G,基准速度为3.4GHz,16核,程序运行软件环境为MATLAB R2021a。

2.1 训练与测试设置

线下训练集和线上测试集中包含三层和五层模型,其中,三层模型电阻率分布特征为高—低—高,五层模型电阻率分布特征为高—低—高—低—高,其各层厚度和电阻率参数设置见表3、表4,线上预测的测试集属于训练集的子集。线上训练和线上预测的所有初始模型电阻率均为100 Ω·m。

表3   三层模型的训练集和测试集参数设置

Table 3  Parameter setting for training and testing set of three-layer model

参数训练集测试集
ρ1/(Ω·m)300~600300~500
ρ2/(Ω·m)30~20050~150
ρ3/(Ω·m)300~600400~600
h1/m100~300100~250
h2/m100~300100~250
个数102450

新窗口打开| 下载CSV


表4   五层模型的训练集和测试集参数设置

Table 4  Parameter setting for training and testing set of five-layer model

参数训练集测试集
ρ1/(Ω·m)300~600300~500
ρ2/(Ω·m)50~15060~140
ρ3/(Ω·m)200~300200~300
ρ4/(Ω·m)20~10030~90
ρ5/(Ω·m)300~600300~500
h1/m50~15080~150
h2/m50~10050~100
h3/m100~200120~180
h4/m100~200100~200
个数102450

新窗口打开| 下载CSV


训练之前需要进行预处理工作,将3层、5层模型的设定参数重新划分到反演所需的层数,这样才能保证训练的平均下降梯度矩阵与预测阶段的梯度矩阵是相同大小。在训练和预测时,SOTEM仿真数据中加入了均值为0、标准偏差为0.1 nT/s的高斯噪声,图3展示了部分测试样本的磁场响应数据。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   部分测试样本的仿真数据

Fig.3   Simulation data of some test samples


2.2 训练与预测的统计记录

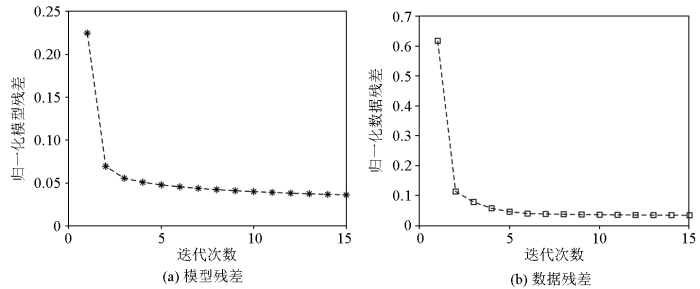
在线下训练阶段,设置最大迭代步数为15步。训练中,模型残差rmsm和数据残差rmsd随着迭代的收敛情况如图4所示,可以看出,两种残差在训练前几步下降非常快,基本上在10步后可收敛至较低水平。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   线下训练的残差收敛曲线

Fig.4   Convergence curve of offline training


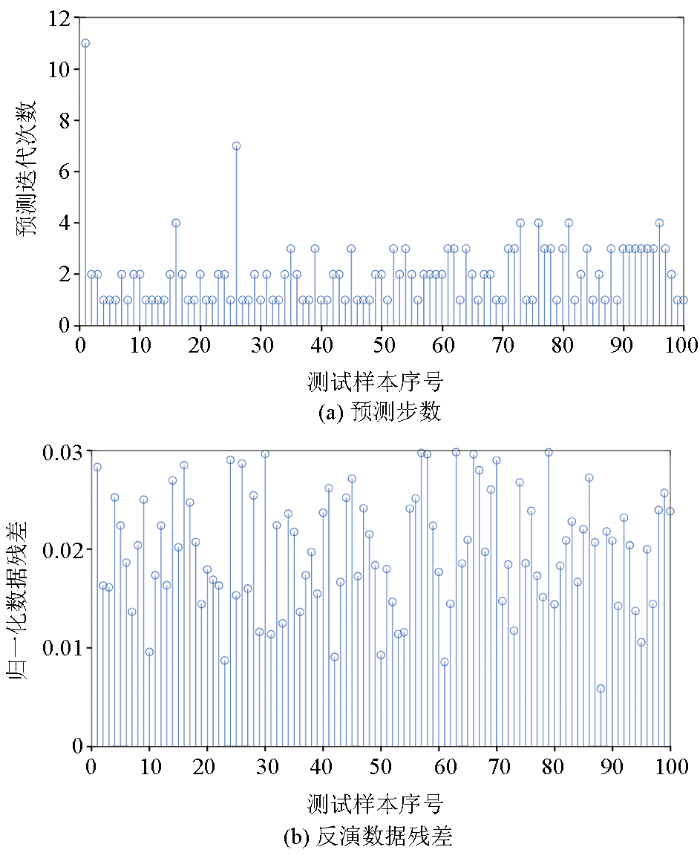
在线上预测阶段也设置最大迭代次数为15。图5给出了所有测试样本反演的预测步数和最终数据残差,可以看出,除个别样本外,绝大多数测试样本能在5步以内收敛,测试样本的反演数据残差均在3%以下。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   线上预测的预测步数与数据残差

Fig.5   Predicting steps and data residual of online predicting


在时间统计上,线下训练阶段,在2 048个训练样本上耗时34 min,获得了15个平均下降方向矩阵K~;线上预测阶段,耗时172 s产生了100个预测结果,平均反演时间1.7 s。

2.3 反演结果对比与分析

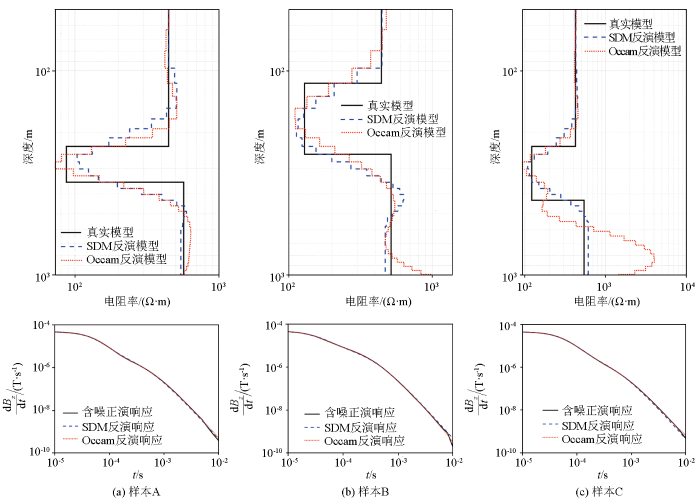
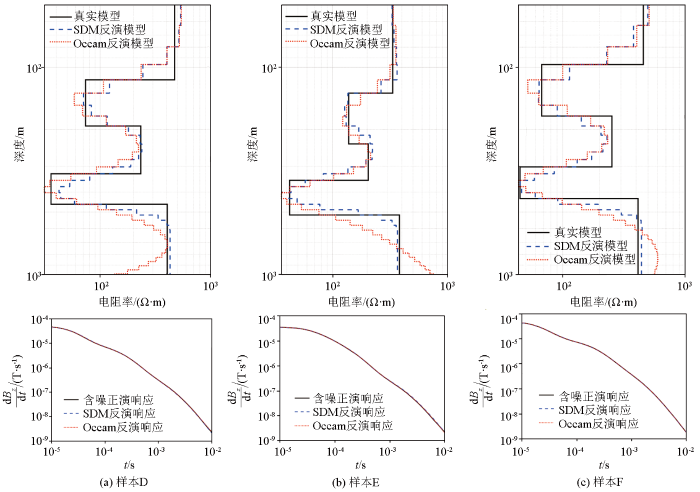
为了展示监督下降法预测结果的准确性与高效性,使用传统Occam算法对测试集的100个样本进行反演,并将其反演模型与监督下降法的反演模型进行对比。图6给出了三层模型中3个样本(样本A、B、C)的真实模型与反演模型对比,以及含噪正演响应与反演响应;图7给出了五层模型中3个样本(样本D、E、F)的真实模型与反演模型对比,以及含噪正演响应与反演响应。可以看出:监督下降法的线上预测模型与真实模型吻合良好,能较准确反映低阻异常的深度和电阻率;Occam算法的反演结果大体上也与真实模型吻合,但其下边界比监督下降法更模糊,这是因为监督下降法在线上训练时将边界快速变化信息隐含在下降方向中。此外,由于三层模型测试数据的晚期噪声较大,Occam算法的反演结果在深层出现大范围波动,对真实模型的反映并不准确,而监督下降法通过融合先验信息能够在一定程度上抑制噪声的影响,提高预测结果的稳定性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   三层模型3个样本的模型及其含噪正演响应与反演响应

Fig.6   Real model response with noise and inversion model response of 3 samples for three-layer model


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   五层模型3个样本的模型及其含噪正演响应与反演响应

Fig.7   Real model response with noise and inversion model response of 3 samples for five-layer model


在反演效率上,Occam算法对每个样本的平均反演时间为23 s,相比之下,基于监督下降法的SOTEM线上预测反演比传统Occam算法快13倍左右。效率的大幅提升主要是省去了雅可比矩阵计算的时间,以及迭代次数更少。

3 结论

本文探索了一种融合物理建模与数据驱动的反演方法,将机器学习中监督下降法应用于SOTEM数据反演中,以提高SOTEM反演的精度和效率,并兼顾可靠的泛化能力。相较于基于深度学习的融合式反演方法,本文基于机器学习中监督下降法实现了融合式反演方法,在线下训练和线上预测时采用了传统的反演迭代框架,通过数据残差计算融入物理建模,算法复杂度降低,训练过程简单,更易于实现。

目前,本文基于采用层状大地模型构建训练集和测试集,实现了基于监督下降法的SOTEM数据一维反演,构建了基于监督下降法的融合式SOTEM反演框架。在此基础上,考虑从以下3个方面完善融合式反演方法:①进一步研究强先验与弱先验信息下最优训练集设计,尤其是通用性更强的弱先验信息训练集,尝试通过包含多种最简单情况,使得平均下降方向学习如何区分数据中存在模型边界上升、下降的能力,从而重建其他任意情况;②将正则化引入线上预测中,利用不同模型约束对预测模型进行微调,降低多解性,消除伪异常;③基于监督下降法开展SOTEM高维反演研究,以期推动SOTEM高维反演的实用化。

参考文献

底青云, 朱日祥, 薛国强, 等.

我国深地资源电磁探测新技术研究进展

[J]. 地球物理学报, 2019, 62(6):2128-2138.

DOI:10.6038/cjg2019M0633      [本文引用: 1]

诸多研究表明我国深部资源潜力巨大，但目前的开发开采深度普遍停留在500 m以浅，开展"攻深探盲"是构建国家资源安全体系的有效途径.应用最先进的科学技术手段，提取深部地质信息，已成为我国当前地球物理科学研究的发展方向.作为地球物理学的重要分支，电磁法是矿产资源探查的主体手段之一.在分析我国现阶段航空、地面及海洋电磁探测技术进展的基础上，本文重点说明了极低频电磁法（简称WEM法），多通道瞬变电磁法（简称MTEM）和电性源短偏移瞬变电磁法（简称SOTEM）等电磁探测新技术.WEM法建立一套包括岩石层、大气层和电离层在内的全空间电磁传播理论，通过新研制的观测系统，获取地下10 km的地电信息；MTEM方法是地下埋深4 km目标体精细勘查的有效手段；SOTEM实现地下1.5 km深度范围内目标体的精细探测.通过多种电磁探测技术组合，可实现地下10 km深度范围内多尺度探测，达到"望远镜+放大镜+显微镜"探测效果.同时，本文指出进一步研发与新方法配套的装备、资料处理技术和大数据人工智能识别等将是我国电磁法未来的发展方向.

Di Q Y, Zhu R X, Xue G Q, et al.

New development of the Electromagnetic (EM) methods for deep exploration

[J]. Chinese Journal of Geophysics, 2019, 62(6):2128-2138.

[本文引用: 1]

何继善, 薛国强.

短偏移距电磁探测技术概述

[J]. 地球物理学报, 2018, 61(1):1-8.

DOI:10.6038/cjg2018L0003      [本文引用: 1]

由于人工源电磁探测效果与收发距离有一定关系，本文首先分析了收发距离为零的中心回线源瞬变电磁法（Transient Electromagnetic Method，TEM）视电阻率定义和算法特点，回溯了从圆形回线到矩形的修正式中心回线装置的发展过程；概述了从中心回线发展到接地导线源短偏移瞬变电磁（Short-Offset TEM，SOTEM）理论上的可行性；列举了将LOTEM（Long-Offset TEM）从数倍于探测深度的观测区推进到近源区后的探测实例.对于频率域人工源电磁法，介绍了起源于MT（Magneto-Telluric）的CSAMT（Controlled Source Audio-frequency Magneto-Telluric）与电磁频率测深法不同发展道路.电磁频率测深将观测区从远区推进到了中区；广域电磁法通过全区视电阻率新定义不仅提高了解释精度，而且将传统CSAMT远场观测模式推进到中区探测模式；最后指出，如能采用新的点微元假设计算方法，可有望分离自有场和辐射场，实现频域电磁近源探测.

He J S, Xue G Q.

Review of the key techniques on short-offset electromagnetic detection

[J]. Chinese Journal of Geophysics, 2018, 61(1):1-8.

[本文引用: 1]

卢云飞, 薛国强, 邱卫忠, 等.

SOTEM研究及其在煤田采空区中的应用

[J]. 物探与化探, 2017, 41(2):354-359.

[本文引用: 1]

Lu Y F, Xue G Q, Qiu W Z, et al.

The research on SOTEM and its application in mined-out area of coal mine

[J]. Geophysical and Geochemical Exploration, 2017, 41(2):354-359.

[本文引用: 1]

Xue G Q, Chen W Y, Yan S.

Research study on the short offset time-domain electromagnetic method for deep exploration

[J]. Journal of Applied Geophysics, 2018,155:131-137.

[本文引用: 1]

Guo Z W, Xue G Q, Liu J X, et al.

Electromagnetic methods for mineral exploration in China:A review

[J]. Ore Geology Reviews, 2020,118:103357.

[本文引用: 1]

陈大磊, 陈卫营, 郭朋, 等.

SOTEM法在城镇强干扰环境下的应用——以坊子煤矿采空区为例

[J]. 物探与化探, 2020, 44(5):1226-1232.

[本文引用: 1]

Chen D L, Chen W Y, Guo P, et al.

The application of SOTEM method to populated areas:A case study of Fangzi coal mine goaf

[J]. Geophysical and Geochemical Exploration, 2020, 44(5):1226-1232.

[本文引用: 1]

林君, 薛国强, 李貅.

半航空电磁探测方法技术创新思考

[J]. 地球物理学报, 2021, 64(9):2995-3004.

DOI:10.6038/cjg2021P0409      [本文引用: 1]

最新的成矿理论研究和深部定位预测结果均表明我国大陆2000 m深部蕴藏着潜力巨大的矿产资源，为在辽阔的国土面积上实现大深度、高精度、广覆盖地球物理探测，开展半航空电磁探测方法与技术研究显得十分必要.本文总结了国内外半航空电磁法的发展现状，重点围绕方法与装备技术等问题进行讨论，并对近年来的最新成果，如：时频协同探测、半航空短偏移距探测、无人机编队观测等新模式，深度学习去噪、多发射源视电阻率定义、拟地震成像等进行了系统分析.最后，对半航空电磁法的发展方向进行了展望，指出任意码形大功率发射和三维高分辨成像等方法技术是下一步的关键突破方向，有望在深部地质找矿、灾害预警和城市地下深部勘查等方面发挥重要作用.

Lin J, Xue G Q, Li X.

Technological innovation of semi-airborne electromagnetic detection method

[J]. Chinese Journal of Geophysics, 2021, 64(9):2995-3004.

[本文引用: 1]

张莹莹.

电性源瞬变电磁法综述

[J]. 物探与化探, 2021, 45(4):809-823.

[本文引用: 1]

Zhang Y Y.

Review on the study of grounded-source transient electromagnetic method

[J]. Geophysical and Geochemical Exploration, 2021, 45(4):809-823.

[本文引用: 1]

陈卫营, 薛国强, 崔江伟, 等.

SOTEM响应特性分析与最佳观测区域研究

[J]. 地球物理学报, 2016, 59(2):739-748.

DOI:10.6038/cjg20160231      [本文引用: 1]

电性源短偏移距瞬变电磁法(SOTEM)是目前研究和应用较为广泛的一种人工源时间域电磁法工作装置,对深部资源地球物理精细探测具有一定的实际意义.为了深入理解方法内涵并更好地进行推广应用,本文基于电性源瞬变电磁一维正演理论,研究了SOTEM地下感应电流扩散、多分量电磁响应平面分布、多偏移距衰减等特性,然后根据上述特性研究了SOTEM的最佳观测区域.研究结果表明:电性源在地下可以产生水平和垂直两个方向的感应电流.其中,水平感应电流又分为上部水平感应电流和下部水平感应电流(又称作返回电流),水平感应电流的极大值主要集中于发射源附近并垂直向下扩散;垂直感应电流极大值沿与地面呈45&#176;角的方向向下、向外扩散,并且具有较低的振幅和较快的扩散速度.电性源激发的六个方向的电磁场分量都具有一定的探测能力,但是考虑到地面观测的方便性和各分量的传播、分布特点,大多数情况仅利用垂直磁场分量H<sub>z</sub>(&#240;B/&#240;t)和水平电场分量E<sub>x</sub>.其中,H<sub>z</sub>仅对低阻目标体敏感,且敏感区域位于赤道向区域,并集中在发射源附近;E<sub>x</sub>既对低阻体敏感也对高阻体敏感,对低阻体的敏感区域位于赤道向区域,而对高阻体的敏感区域位于轴向区域,并且敏感区域距发射源的距离与目标体埋深和围岩电性有关.

Chen W Y, Xue G Q, Cui J W, et al.

Study on the response and optimal observation area for SOTEM

[J]. Chinese Journal of Geophysics, 2016, 59(2):739-748.

[本文引用: 1]

薛俊杰, 陈卫营, 王贺元.

电性源短偏移瞬变电磁探测深度分析与应用

[J]. 物探与化探, 2017, 41(2):381-384.

[本文引用: 1]

Xue J J, Chen W Y, Wang H Y.

Analysis and application of the detection depth of electrical source Short-offset TEM

[J]. Geophysical and Geochemical Exploration, 2017, 41(2):381-384.

[本文引用: 1]

常江浩, 薛国强.

电性源短偏移距瞬变电磁场扩散规律三维数值模拟

[J]. 地球科学与环境学报, 2020, 42(6):711-721.

[本文引用: 1]

Chang J H, Xue G Q.

Three-dimensional numerical simulation of diffusion law of short-offset grounded-wire transient electromagnetic field

[J]. Journal of Earth Sciences and Environment, 2020, 42(6):711-721.

[本文引用: 1]

陈卫营, 李海, 薛国强, 等.

SOTEM数据一维OCCAM反演及其应用于三维模型的效果

[J]. 地球物理学报, 2017, 60(9):3667-3676.

DOI:10.6038/cjg20170930      [本文引用: 1]

本文基于垂直磁场分量研究了SOTEM数据的一维OCCAM反演方法，并将其应用于理论三维数据及野外实测数据的反演.对于大部分一维模型，OCCAM反演可取得较好的反演效果，且反演结果不依赖于偏移距；噪声对SOTEM数据的OCCAM反演具有较大影响，但当信号含噪水平不超过5%时，反演结果仍具有较好的准确性；若浅层存在较厚的低阻层，OCCAM反演结果对下部地层的分辨能力下降，仅能获得具有平均效应的电阻率.将一维算法应用于SOTEM三维数据的反演，会产生较大的误差，尤其是在异常体边缘地带影响最为严重.该影响程度与异常体和背景电阻率之间的差异有关，对于大多数电性近似呈连续变化的真实大地而言，一维OCCAM反演算法仍可获得较好的效果.最后通过陕西某煤田深部富水性调查的实测SOTEM数据反演验证了本文的研究成果.

Chen W Y, Li H, Xue G Q, et al.

1D OCCAM inversion of SOTEM data and its application to 3D models

[J]. Chinese Journal of Geophysics, 2017, 60(9):3667-3676.

[本文引用: 1]

宋婉婷, 陈卫营.

SOTEM数据拟二维反演研究与应用

[J]. 地球科学与环境学报, 2022, 44(1):132-142.

[本文引用: 1]

Song W T, Chen W Y.

Study on quasi-2D inversion for SOTEM data and its application

[J]. Journal of Earth Sciences and Environment, 2022, 44(1):132-142.

[本文引用: 1]

Guo R, Wu X, Liu L H, et al.

Adaptive sharp boundary inversion for transient electromagnetic data

[J]. Progress in Electromagnetics Research M, 2017,57:129-138.

[本文引用: 1]

Zhdanov M S.

Marine electromagnetic methods

[G]//Foundations of geophysical electromagnetic theory and methods. Amsterdam:Elsevier,2018:625-662.

[本文引用: 1]

苏扬, 殷长春, 刘云鹤, 等.

基于广义模型约束的时间域航空电磁反演研究

[J]. 地球物理学报, 2019, 62(2):743-751.

DOI:10.6038/cjg2019M0217      [本文引用: 1]

由于航空电磁具有海量数据，因此快速有效的成像和反演手段至关重要.本文针对层状介质模型推导与实现了广义模型约束条件下时间域航空电磁一维反演.从正则化反演的目标函数出发，通过改变模型约束项构造Lp范数反演和聚焦反演，进而通过改变模型求解域构造出基于小波变换的稀疏约束反演.针对不同反演方法目标函数的构建方式，本文进一步从数学原理上分析不同反演方法的预期效果，并通过理论模型和实测数据进行验证.结果表明L0.8范数反演、聚焦反演和基于小波变换的稀疏约束反演可以得到更符合地下层状介质陡变界面的反演结果.

Su Y, Yin C C, Liu Y H, et al.

Inversions of time-domain airborne EM based on generalized model constraints

[J]. Chinese Journal of Geophysics, 2019, 62(2):743-751.

[本文引用: 1]

孙怀凤, 张诺亚, 柳尚斌, 等.

基于L1范数的瞬变电磁非线性反演

[J]. 地球物理学报, 2019, 62(12):4860-4873.

DOI:10.6038/cjg2019M0690      [本文引用: 1]

瞬变电磁反演存在高度的非线性特征，常用的最小二乘等线性反演方法往往对初始模型高度依赖，并且极易陷入局部最优解.本文基于观测数据与模拟数据的L1范数建立目标函数，采用模拟退火非线性全局最优化方法实现瞬变电磁一维反演.初始模型完全随机产生，通过指数函数退温机制模拟系统能量最小实现迭代，通过接收概率函数评价当前模型，实现局部最优解的跳出，最终实现全局最优化求解.通过数值算例发现，无论给定的反演层数等于还是大于设计模型，都可以获得较好的反演效果，因而可以在反演初始就设计较多的层数，实现反演模型的自动拟合；同时，利用含噪声数据反演进一步验证算法的稳定性.最后，对实测数据进行了反演测试，结果与钻孔编录基本一致，表明提出的基于L1范数的模拟退火反演可用于实测数据处理.

Sun H F, Zhang N Y, Liu S B, et al.

L1-norm based nonlinear inversion of transient electromagnetic data

[J]. Chinese Journal of Geophysics, 2019, 62(12):4860-4873.

[本文引用: 1]

Rao L T, Wu X, Guo R, et al.

A comparative study of different stabilizers for retrieving geoelectric structure based on a unified framework

[J]. Journal of Applied Geophysics, 2020,175:104001.

[本文引用: 1]

Araya P M, Jennings J, Adler A, et al.

Deep learning tomography

[J]. The Leading Edge, 2018, 37(1):5866.

[本文引用: 1]

Tan C, Luy S H, Dong F, et al.

Image reconstruction based on convolutional neural network for electrical resistance tomography

[J]. IEEE Sensors Journal, 2019, 19(1):196-204.

[本文引用: 1]

Mandija S, Meliadò E F, Huttinga N R F, et al.

Opening a new window on MR-based Electrical Properties Tomography with deep learning

[J]. Scientific Reports, 2019,9:8895.

[本文引用: 1]

Li X Y, Zhou Y, Wang J M, et al.

A novel deep neural network method for electrical impedance tomography

[J]. Transactions of the Institute of Measurement and Control, 2019, 41(14):4035-4049.

DOI:10.1177/0142331219845037      [本文引用: 1]

Image reconstruction for Electrical Impedance Tomography (EIT) is a highly nonlinear and ill-posed inverse problem. It requires the design and employment of feasible reconstruction methods capable to guarantee trustworthy image generation. Deep Neural Networks (DNN) have a powerful ability to express complex nonlinear functions. This research paper introduces a novel framework based on DNN aiming to achieve EIT image reconstruction. The proposed DNN model, comprises of the following two layers, namely: The Stacked Autoencoder (SAE) and the Logistic Regression (LR). It is trained using the large lab samples which are obtained by the COMSOL simulation software (a cross platform finite elements analysis solver). The relationship between the voltage measurement and the internal conductivity distribution is determined. The untrained voltage measurement samples are used as input to the trained DNN, and the output is an estimate for image reconstruction of the internal conductivity distribution. The results show that the proposed model can achieve reliable shape and size reconstruction. When white Gaussian noise with a signal-to-noise ratio of 30, 40 and 50 were added to test set, the proposed DNN structure still has good imaging results, which proved the anti-noise capability of the network. Furthermore, the network that was trained using simulation data sets, would be applied for the EIT image reconstruction based on the experimental data that were produced after preprocessing.

Wu Y, Lin Y Z.

InversionNet:An efficient and accurate data-driven full waveform inversion

[J]. IEEE Transactions on Computational Imaging, 2020,6:419-433.

[本文引用: 1]

Ongie G, Jalal A, Metzler C A, et al.

Deep learning techniques for inverse problems in imaging

[J]. IEEE Journal on Selected Areas in Information Theory, 2020, 1(1):39-56.

[本文引用: 1]

Raissi M, Perdikaris P, Karniadakis G E.

Physics-informed neural networks:A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations

[J]. Journal of Computational Physics, 2019,378:686-707.

[本文引用: 1]

Jin Y C, Shen Q Y, Wu X Q, et al.

A physics-driven deep-learning network for solving nonlinear inverse problems

[J]. Petrophysics:The SPWLA Journal of Formation Evaluation and Reservoir Description, 2020, 61(1):86-98.

[本文引用: 1]

Guo R, Li M K, Yang F, et al.

Application of supervised descent method for 2D magnetotelluric data inversion

[J]. Geophysics, 2020, 85(4):WA53-WA65.

[本文引用: 1]

Colombo D, Turkoglu E, Li W C, et al.

Physics-driven deep-learning inversion with application to transient electromagnetics

[J]. Geophysics, 2021, 86(3):E209-E224.

[本文引用: 1]

Bang M, Oh S, Noh K, et al.

Imaging subsurface orebodies with airborne electromagnetic data using a recurrent neural network

[J]. Geophysics, 2021, 86(6):E407-E419.

[本文引用: 1]

Lu S, Liang B Y, Wang J W, et al.

1-D inversion of GREATEM data by supervised descent learning

[J]. IEEE Geoscience and Remote Sensing Letters, 2022,19:3053247.

[本文引用: 1]

Asif M R, Foged N, Maurya P K, et al.

Integrating neural networks in least-squares inversion of airborne time-domain electromagnetic data

[J]. Geophysics, 2022, 87(4):E177-E187.

[本文引用: 1]

Xiong X H, De la Torre F.

Supervised descent method and its applications to face alignment

[C]// 2013 IEEE Conference on Computer Vision and Pattern Recognition,2013:532-539.

[本文引用: 1]

Nabighian M N. 勘查地球物理电磁法:第1卷理论[M]. 赵经祥等,译. 北京: 地质出版社,1992.

[本文引用: 1]

Nabighian M N. Electromagnetic Methods in Applied Geophysics Volume 1,Theory[M].Translated by Zhao J X,et al. Beijing: Geology Press,1992.

[本文引用: 1]

Guptasarma D, Singh B.

New digital linear filters for Hankel J0 and J1 transforms

[J]. Geophysical Prospecting, 1997, 45(5):745-762.

[本文引用: 1]

Knight J H.

Transient electromagnetic calculations using the gaver-stehfest inverse laplace transform method

[J]. Geophysics, 1982, 47(1):47.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com