E-mail Alert Rss
 

物探与化探, 2023, 47(3): 766-774 doi: 10.11720/wtyht.2023.1241

方法研究·信息处理·仪器研制

基于机器学习松辽盆地大地热流计算与特征分析

宫明旭,1, 白利舸2, 曾昭发,2, 吴丰收1

1.中船勘察设计研究院有限公司,上海 200063

2.吉林大学 地球探测科学与技术学院,吉林 长春 130026

Machine learning-based calculation and characteristic analysis of terrestrial heat flow in the Songliao Basin

GONG Ming-Xu,1, BAI Li-Ge2, ZENG Zhao-Fa,2, WU Feng-Shou1

1. China Ship Survey and Design Institute Co.,Ltd.,Shanghai 200063,China

2. College of Geo-Exploration Science and Technology,Jilin University,Changchun 130026,China

通讯作者: 曾昭发(1966-),男,广西全州人,教授,博士生导师,博士,研究方向为应用地球物理。Email:zengzf@jlu.edu.cn

第一作者: 宫明旭(1993-),男,硕士研究生,从事地球物理探测与评价的研究工作。Email:1209686360@qq.com

责任编辑: 叶佩

收稿日期: 2022-05-20   修回日期: 2023-04-7  

基金资助: 国家自然科学基金项目“深部超临界热储流体—岩石综合电性特征与电磁响应研究”(42074119)

Received: 2022-05-20   Revised: 2023-04-7  

摘要

大地热流是地球内部热量在地表的直接显示,对地热资源评估具有极高的参考价值,由于传统利用钻井技术的热流测定方法既昂贵又困难,至今松辽盆地仍未能实现高质量、高分辨率的大地热流测量。机器学习是一种用于数据分析的技术,它可以识别数据中的模式并将其用于自动计算未知数据。本文引入机器学习方法来计算区域大地热流。这项研究基于全球大地热流实测数据与地质构造数据,首先采用了Kriging回归算法和机器学习算法计算某已知热流分布区域的大地热流,并计算了均方根误差和相关系数,表明机器学习算法能获得误差更小、相关度更高的结果。随后使用机器学习方法计算了松辽盆地的大地热流值。计算结果显示盆地中部大地热流最高,以大庆、松原之间的区域为中心呈环状向外逐渐变低,中心区域大地热流超过80 mV/m2。该结果与区域实测地温梯度测量结果具有良好一致性,为进一步分析松辽盆地地热资源分布规律提供参考。最后,利用Sobol方法进行地质特征灵敏度分析,量化各参数的影响。本文的研究表明机器学习方法在大地热流值计算方面具有较高的研究和应用价值。

关键词： 松辽盆地; 大地热流; 机器学习; 地热资源分布

Abstract

Terrestrial heat flow has a high reference value for the evaluation of geothermal resources since it can directly indicate the Earth's internal heat on the surface.However,no high-quality and high-resolution terrestrial heat flow measurements have been conducted in the Songliao Basin due to costly and difficult conventional heat flow measurements based on the drilling technology.Machine learning,as a technology for data analysis,can identify patterns in data and utilize these patterns to automatically calculate unknown data.This study calculated the regional terrestrial heat flow using the machine learning method.Based on the measured data of global terrestrial heat flow and the geological structure data,both the Kriging regression algorithm and the machine learning algorithm were used to calculate the terrestrial heat flow in a known heat flow distribution area,as well as the root mean square error and the correlation coefficient.The machine learning algorithm yielded results with a smaller error and a higher correlation.Then,the terrestrial heat flow in the Songliao Basin was calculated using the machine learning method.As revealed by the calculation results,the terrestrial heat flow is the highest (more than 80 mWm-2) in the Songliao basin and gradually decreases outward in a circular pattern centered on the area between Daqing and Songyuan.The results are highly consistent with the measured results of the regional geothermal gradient,providing a reference for further analysis of the distribution patterns of geothermal resources in the Songliao Basin.Finally,the sensitivity of geological characteristics was analyzed using the Sobol method to quantify the effects of various parameters.This study verifies that the machine learning method has a high research and application value in the calculation of terrestrial heat flow.

Keywords： Songliao Basin; terrestrial heat flow; machine learning; distribution of geothermal resources

PDF (6079KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

宫明旭, 白利舸, 曾昭发, 吴丰收. 基于机器学习松辽盆地大地热流计算与特征分析[J]. 物探与化探, 2023, 47(3): 766-774 doi:10.11720/wtyht.2023.1241

GONG Ming-Xu, BAI Li-Ge, ZENG Zhao-Fa, WU Feng-Shou. Machine learning-based calculation and characteristic analysis of terrestrial heat flow in the Songliao Basin[J]. Geophysical and Geochemical Exploration, 2023, 47(3): 766-774 doi:10.11720/wtyht.2023.1241

0 引言

大地热流是地球内单位时间和面积向地表传输的热量,是地热资源研究中极具参考价值的指标。如何获取或计算区域大地热流对地热资源勘探和开采具有十分重要的意义。

通常,人们通过钻井钻取岩心测得岩石热导率,再通过地温测量与岩石热导率间接计算大地热流,这种方法昂贵且困难,在没有钻孔的位置就无法得知其大地热流,限制了大范围的热流获取,无法获得高分辨率区域大地热流分布信息。所以国内外学者们一直致力于寻找更便捷、有效的方法获得大地热流。美国学者Lerche等[1]利用沉积地层中镜质体的反射率计算区域大地热流,引起了国内外学者的关注,但该方法要求目标区域的古热流必须为线性变化,地质条件不能太复杂,导致其缺乏普遍适用性。国内学者庞雄奇等[2]对Lerche l模型进行了深入研究并取得了突破性进展,使其适用于复杂、非线性变化条件下的古热流的计算,并成功应用到松辽盆地中。上述方法虽好,却是对古热流的研究计算。魏东平等[3]和董文杰等[4]利用长期气象地温资料计算大地热流,该方法需假设地下介质为水平均匀的,实用性较低。 Fox等[5]使用磁场模型推断南极洲地热通量。Martos等[6]利用热导率和放射性产热量的平均值,根据居里面深度计算了地表热流,其采取统一的热参数使得计算结果精度较低。唐晗晗等[7]采用迭代的方法,利用多项地热参数之间的联系,计算出了热导率的横向分布改进了Martos的方法,估算出的热流值更加准确。

目前松辽盆地大热热流在很大程度上是未知的,由以上可知目前热流获取方法可分为3类:①钻井资料收集;②气象地温资料计算;③单一地球物理方法反演计算。前两者费用高、耗时长且实现困难。第3种方法实现相对容易,但地热是地质构造综合作用的结果,单一地球物理方法取得的结果太片面且难以具备说服力,显然,应建立一个兼顾实测数据和区域地质构造特征的新方法。统计学方法[8]估算全球大地热流逐渐走进学者们的视野,各种适合于表征热流的特征用来预测未测量区域的大地热流。Rezvanbehbahani等[9]首次将机器学习技术应用到大地热流估算中,其核心是训练梯度提升回归树模型在大地热流与所有地质构造信息之间建立相关关系,然后利用训练好的模型预测只有少量实测热流区域的热流。Lucazeau[10]通过经验选择14个地质和地球物理观测数据的最佳值,更新了1993年Pollack等汇编的全球大地热流模型,此外,作者研究表明附加的地质和地球物理信息与地质年龄相结合可以进行更准确的预测。Haklidir[11]基于地热是地质构造综合作用的思想,通过区域地质、化学等数据利用深度学习方法来计算地层温度的新方法,具有很高的研究价值。Lösing等[12]针对机器学习估算局部热流方法中地球物理和地质特征主要是全球数据集,由于数据覆盖范围有限,在极地地区往往具有不可靠的问题,探索使用南极洲和冈瓦纳附近的区域数据集来改进预测,获得的新南极洲热流图显示了更多热流变化信息,并与周围地区耦合边缘有明显联系。目前,机器学习在地热和地球物理领域的应用仍在发展中,国内学者还没有人将机器学习引入到大地热流的计算。本文参考前人的的研究思路,开展基于机器学习的松辽盆地大地热流值计算研究,所采用的模型是深度学习网格,该模型收录在Matlab19及以上版本中,使用更方便,训练速度快,结果精度高。计算时,尽可能地收集全球大地热流实测数据与地质构造特征数据,并添加了三组松辽盆地本地地质构造数据,包括莫霍面深度[13]、岩石圈—软流圈边界[14]和地壳厚度[15]。本文首先对该模型算法性能进行可靠性评估,在此基础上计算了松辽盆地的大地热流值,并结合区域地温梯度进行进一步的特征分析,最后使用Sobol方法进行特征参数灵敏度分析。

1 机器学习方法计算大地热流值

1.1 原理

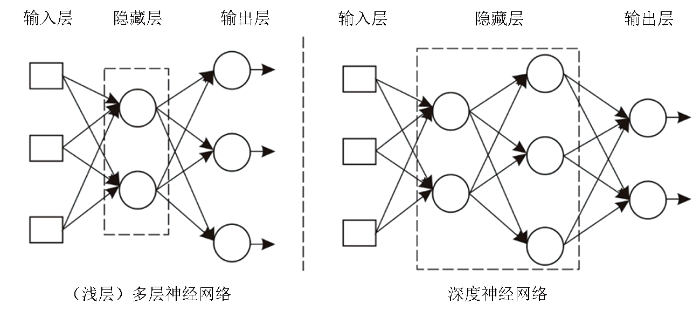
作为人工智能的一个分支,机器学习无需显式编程,它利用已有数据进行自动建模,依据统计理论使计算机在可用的数据中进行学习[16]。识别数据中的规律与特点,将其规定为一种特定的模式,称之为建模,最后使用这个模型对未知的数据点进行预测。机器学习主要分强化、监督和无监督三大类型。监督学习采用多对输入和正确的输出训练数据的方式[17]。三种类型有各自的应用特点和适用范围,本文采用了应用更广泛的监督学习的方式。机器学习在长期发展中总结出了一种高级的监督学习方法——深度学习(DNN),它克服了深度神经网络迭代过程中因网络层数增加导致的过拟合和梯度消失等问题,使计算效率更高,结果更准确。

神经网络由节点连接而成,单节点表示如下:

z=∑i=1mωixi+b

其中:z为输入数据的加权和;m输入数据类型数量;ωi为节点i的权重;xi为输入节点i的数据;b为偏差。最后,加权和输入到激活函数,获得输出,即

y=φ(z)

式中φ(·)为激活函数。大量的节点的连接组成了神经网络(图1),它是一种层级结构,包含输入层、隐藏层和输出层。神经网络按其特点可分为两类: 浅层神经网络和深度神经网络。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   神经网络分类

Fig.1   Neural network classification


在单层神经网络的计算过程中,通常使用增量规则来调整数据权重ω,该规则通过方程可以表示为

ωij←ωij+αeixj

式中:ωij为输出节点i与输入节点j之间的权重;α为学习率(0<α≤1);ei表示节点i的误差。程序运行时,通过反复计算误差、调整权重进行迭代,直到误差达到预先设定好的限值。

但是在多层神经网络中,增量规则出现了梯度消失和过拟合等问题。直到1986年,人们将反向传播算法引入到多层神经网络计算中才解决了这些弊端。反向传播算法首先需要计算最外层输出节点的增量δi:

δi=φ'(zi)ei

式中φ'(·)为φ(·)的导数。从最外层开始反向移动,逐层计算每个隐藏层的增量,然后利用式(5)计算调整各层的权重,重复上述过程,直到误差满足要求为止,最终完成训练。

Δωij=αδixj,ωij=ωij+Δωij。

对我们的训练数据采用上述过程直到训练出满足要求的神经网络,人们将这种学习方式命名为深度学习。

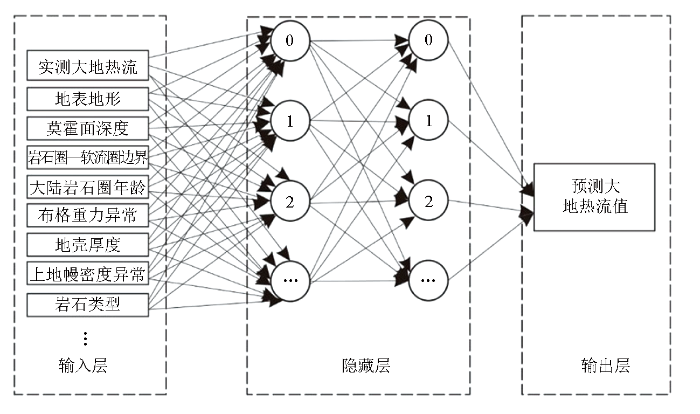
1.2 流程

与其他使用单个地球物理特征[18](重力异常或磁异常)计算大地热流不同,机器学习方法计算大地热流是基于一定种类全球大陆可用的地质构造特征和信息数据(表1)。将所有地质特征数据重新采样到与全球大地热流统一的网格中。利用机器学习的方法在大地热流与地质构造特征之间建立相关关系,然后输入热流未知区域的地质特征数据,最终计算出该区域的大地热流值。这种方法计算出的大地热流值受区域地质情况、构造背景和实测大地热流值的约束,为区域地热资源的分布研究提供一种新方法。

表1   全球参数变量

Table 1  List of global parameter variables

变量名称数据量参考文献
地表地形64800Amante and Eakins(2009)[19]
莫霍面深度64800Reguzzoni et al.(2013)[20];
刘卓(2019)[13]
岩石圈—软流圈边界64800Pasyanos et al.(2014)[21] ;
刘子婧(2016)[14]
大陆岩石圈年龄5365Poupinet and Shapiro(2009)[22]
布格重力异常64800Balmino et al.(2012)[23]
地壳厚度64800Laske et al.(2013)[24];
王开燕等(2015)[15]
上地幔密度异常64800Kaban et al.(2004)[25]
磁异常64800Maus et al.(2013)[26]
上、下地壳厚度64800Bassin(2000)[27]
生热率64800USGS(2016)[28]
上地幔速度结构64800Shapiro and Ritzwoller(2002)[29]
岩石类型64800Hartmann and Moosdorf(2012)[30]
到洋脊的距离64800Coffin et al.(1998)[31]
(UTIG Plates Project)

新窗口打开| 下载CSV


我们采用了深度学习(DNN)模型,根据地质构造特征相关数据合集进行训练,从而估算目标区域的大地热流值(图2),工作流程如图3所示。为了对比机器学习的计算能力,我们还补充了一种经典的统计学算法:Kriging回归算法,采用协方差函数对随机过程/随机场进行空间建模和计算[32]。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   DNN架构

Fig.2   DNN architecture diagram


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   工作流程

Fig.3   Work flow chart


1.3 可靠性评估

为了测试机器学习方法在计算大地热流时的可靠性,我们做了一个试验:在全球数据(图4)中随机选取一块大地热流数据较多的区域(图5),剔除该区域真实已有的热流数据,分别使用机器学习和Kriging回归算法计算该区域的大地热流并与其真实大地热流值进行对比,评估该方法的可靠性。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   全球大地热流值(黑框中为选取区域,据Gosnold W[33]修改)

Fig.4   Global terrestrial heat flow value (the selected area is in the black box,modified according to Gosnold W[33])


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   某区域实测大地热流

Fig.5   Measured earth heat flow in a region


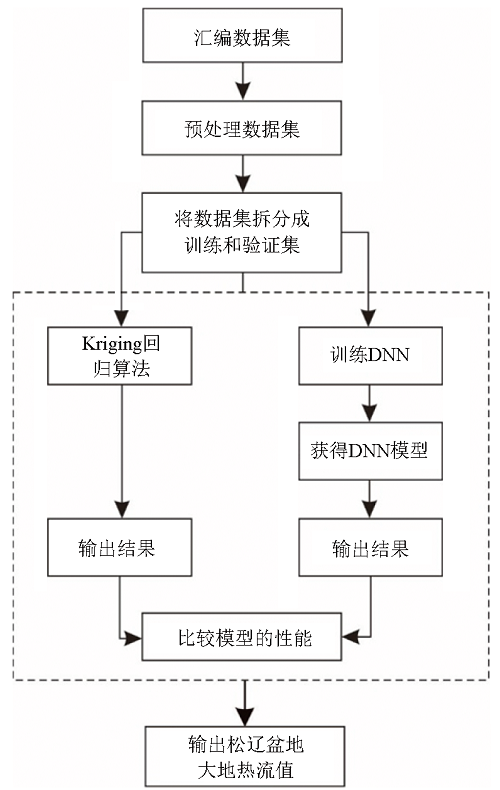
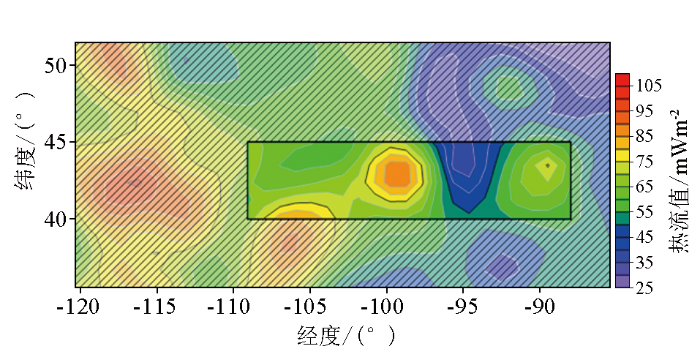
随机选择区域内一定占比的热流数据点,与区域外的热流数据点一起构成训练集,区域内的剩余热流数据点作为验证集。我们在计算大地热流值的同时也给出了它的误差和相关性(RMSE和R)(图6)。

RMSE=1<实测热流><实测热流-估算热流2>

其中可以看出<>代表验证集的平均值。

图6

新窗口打开| 下载原图ZIP| 生成PPT

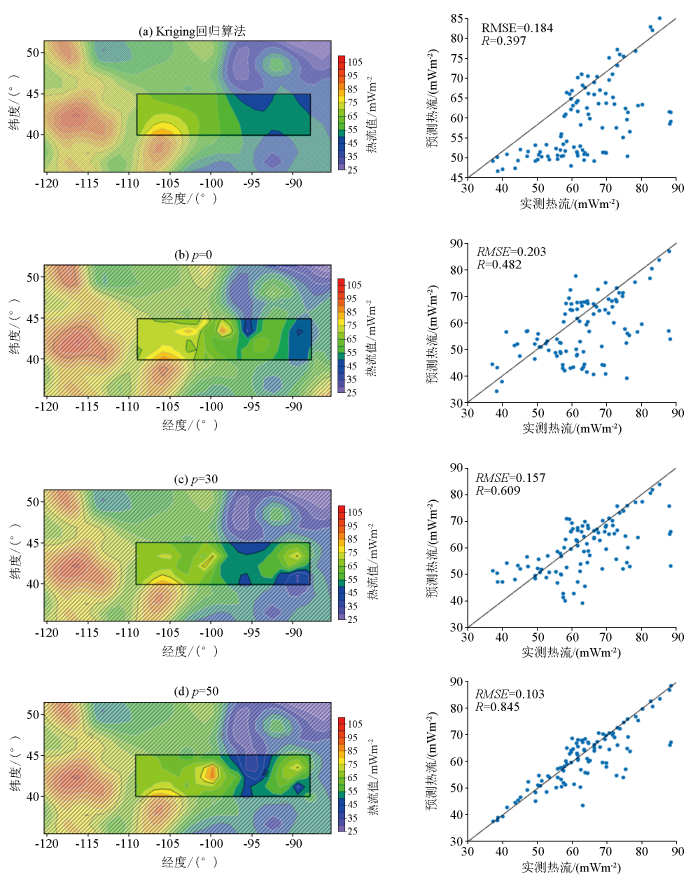
图6   某区域热流Kriging算法和机器学习方法计算结果图(左)及其相关性(右)

Fig.6   Calculation results of Kriging algorithm and machine learning method for heat flow in a region (left) and their correlation (right)


Kriging回归算法的计算结果(图6a)对实测热流(图5)还原效果较差,具有较大的RMSE(0.184)和较小的相关系数R(0.397)。当使用机器学习方法计算热流(ρ=0)时,计算结果(图6c)同样具有较大的RMSE(0.203)和较小的R(0.482),但相对Kriging回归算法具有较高的相关性,这说明机器学习方法在毫无本地训练数据的区域中计算大地热流时能够初步还原真实热流形态,但误差仍然较大,还原能力较低,这突出了区域地质和构造学在热流计算中的重要性。于是,我们接下来研究了机器学习热流计算效果与训练集中加入区域热流样本密度(ρ)的相关程度。研究区域不变,逐渐增大区域训练样本密度ρ,结果如图6c~h所示,随着本地训练样本密度的增大,热流计算结果对真实热流的还原效果越好(更小的RMSE和更大的R),以上研究结果表明:当我们采用机器学习方法计算某一区域的大地热流时,应尽可能地在训练数据中增大该区域已有的真实热流数据密度,从而获得更接近目标区域大地热流真实形态的计算结果。

2 松辽盆地大地热流计算与特征分析

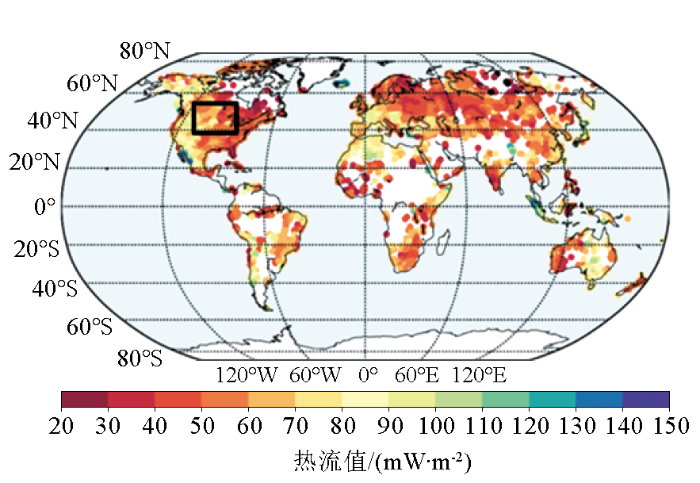
2.1 数据及处理过程

全球的大地热流数据可从北达科他大学提供的国际热流委员会获得[33]数据近似正态分布(图4)。数据的空间分辨率差异很大,首先将全球大地热流和所有可用的地质和构造信息使用1°×1°的经纬度网格中的平均值一一对应,将数据点从35 000减少到4 034个。再将大地热流值限制在100 mWm-2以下,因为松辽盆地目前实测大地热流均小于100 mW·m-2。

目前松辽盆地实测大地热流为吴乾蕃、姜光政等[34-35]以及中国科学院等权威统计收集到的30个大地热流点。我们使用与全球数据相同的网格尺度,这使得松辽盆地的实测热流总个数减少到20个。

2.2 大地热流结果分析

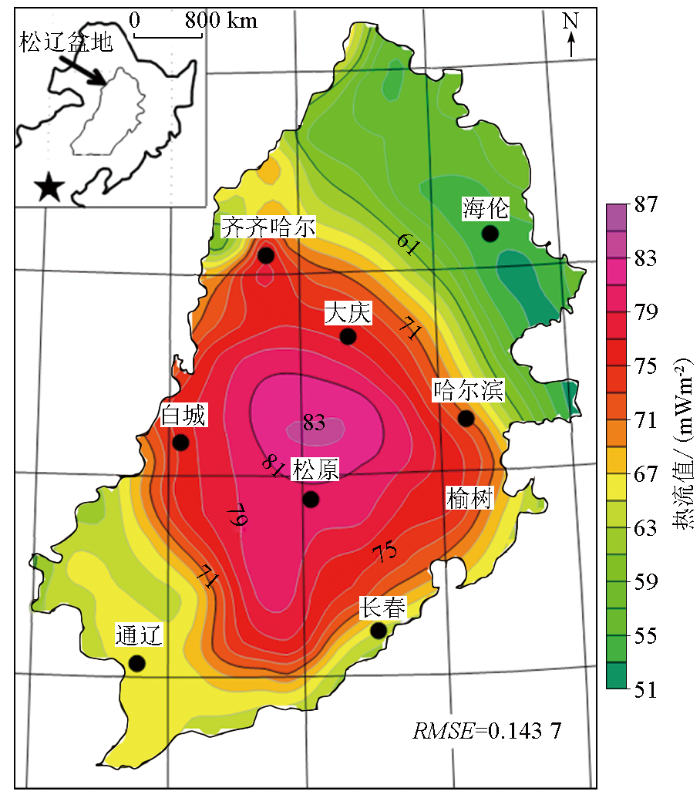
对于松辽盆地,由于本地样本有限,我们将松辽盆地全部实测热流及其对应的地质特征数据加入到样本训练集中。利用机器学习方法对区域大地热流进行计算,迭代12 000次,获得松辽盆地热流分布如图7所示,误差为14.37%。计算结果表明:松辽盆地热流变化特征为中部(松原—大庆)高,热流值超过80 mW·m-2,呈环状向外逐渐降低,向南部有类似为“V”型的热流范围特征,这与松辽盆地NE向的地质构造分布特征相吻合;盆地的北部(海伦)和南部(通辽)热流较低,热流总体变化范围为50~88 mW·m-2。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   松辽盆地大地热流计算结果

Fig.7   Calculation results of terrestrial heat flow in Songliao basin


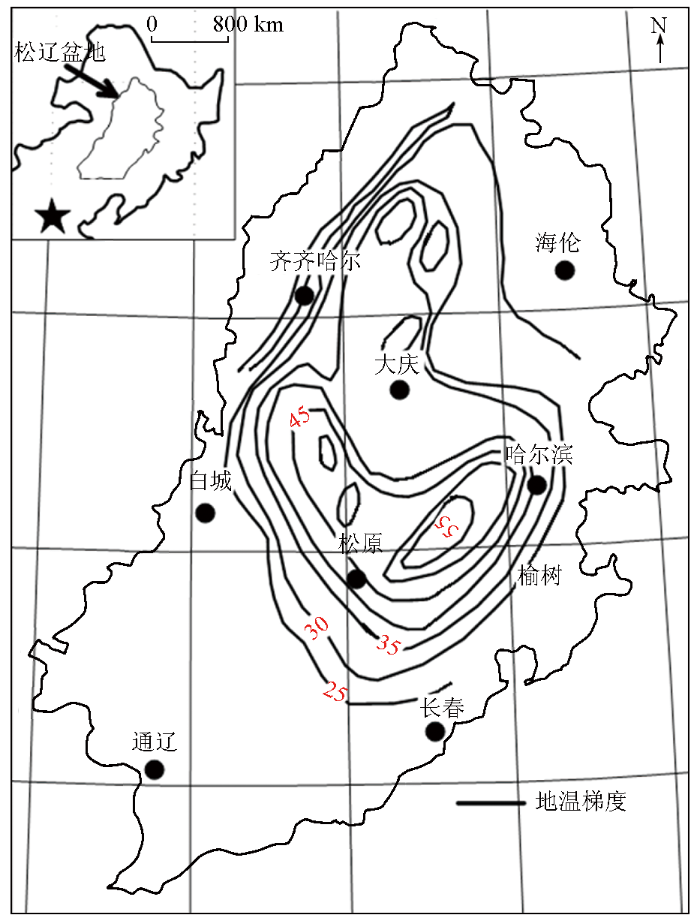
在数学上,大地热流与地温梯度存在正比例关系。本文结合现有的松辽盆地实测地温梯度数据,对基于机器学习松辽盆地大地热流计算结果的可靠性进行探究。

根据刘耀光[36]获得的松辽盆地地温梯度分布特征如图8所示。松辽盆地地温梯度特征表现为哈尔滨、大庆、松原状区域最高,向外逐渐降低;松辽盆地大地热流分布特征表现为中部(大庆—松原)热流最高,向外逐渐降低。这表明松辽盆地实测地温梯度和基于机器学习计算出的大地热流值正相关。说明本文获得的大地热流具有较高的可靠性。此外,He等[37]推断的松辽盆地深部地幔上涌区域与机器学习计算获得大地热流高值区域一致,为该区域大地热流较高提供了佐证[38-39]。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   松辽盆地地温梯度实测等值线[36]

Fig.8   Measured contour map of geothermal gradient in Songliao Basin[36]


2.3 参数特征分析

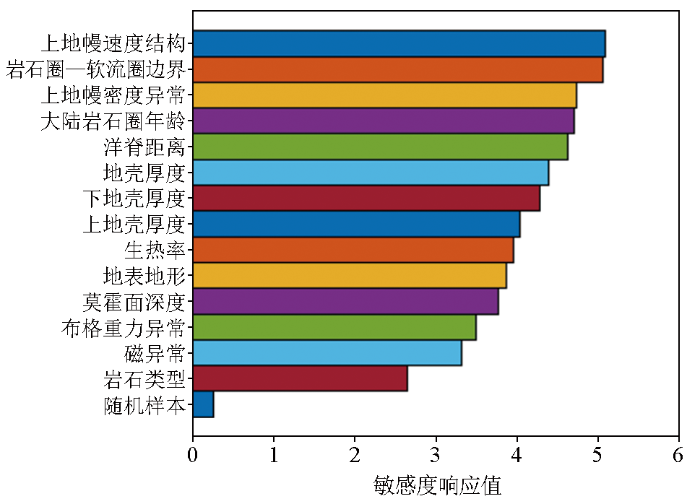
由于松辽盆地实际热流值太少,无法确定每种参数对热流的直接贡献,因此参考使用基于方差的全局敏感度分析方法,即Sobolo方法[40-41],该方法可以提供每个参数及其他参数相互作用对模型输出的影响。

图9中,纵轴为数据参数,横轴为敏感响应程度。由图可知:在14个特征样本中,上地幔速度结构、岩石圈—软流圈边界和上地幔密度等特征对热流贡献值相对最大,这一定程度上表明深部地质构造特征对热流传导具有较为重要的影响。而地壳厚度、生热率等信息可作为次要信息。重磁异常和通过重力反演得到的莫霍面贡献度相对较低,这可能与反演方法及其准确程度有关。岩石类型在14种特征中得分最低,结合该敏感度计算结果一定程度上表明松辽盆地的大地热流主要来源为地球深部热源,深部地质构造(地幔速度结构、密度和LAB界面等)对深部热源向上传导影响较大,而反射性热源(岩石生热率、岩石类型)可作为松辽盆地的次要热源。随机样本为一组随机序列,用于检测方法的正确性,其敏感度小于1,对热流无贡献。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   全球地质特征参数对热流的相对敏感度

Fig.9   Relative sensitivity of global geological characteristic parameters to heat flow


3 结语与讨论

1)使用机器学习算法,可以展示多种地质和构造特征与全球大地热流之间稳定的统计关系。将全球大地热流测量值与松辽盆地可用的大地热流实测值相结合,训练DNN模型获得松辽盆地整个区域的大地热流分布。

2)基于机器学习方法获得的大地热流结果具有许多明显的特征:中部大地热流最高,超过80 mWm-2,表明松辽盆地是一个“热”盆,以松原、大庆为核心呈环状分布,向外逐渐变低,其形态特征与盆地NE向的构造形态相吻合,且与目前已知的区域地温梯度形态正相关,该结果对分析松辽盆地地热资源分布规律和区域地热构造演化具有重要的参考价值。

3)该方法的可靠性评估表明,如果具有更多可用的热流实测值,则计算结果将得到明显提升,通过这种方法可以避免昂贵且困难的现场热流测量,具有高度的深入研究价值。

4)本文通过机器学习对全球尺度参数进行训练,获得了松辽盆地的大地热流分布,该结果相对于传统回归、对抗神经网络算法等不依赖某个地质参数,而是多种地质和构造特征的复杂函数,这更符合地热与当地地质和区域构造环境综合影响的统计关系。但本文训练获得的松辽盆地大地热流结果线性规律较强,难以反演特殊的地质构造,在一定程度上表明,实测大地热流数据较少的情况下,目前的机器学习方法获得的结果可用于区域大尺度热流规律,用于分析小盆地的热异常较为困难。

5)不得不说明的是,目前利用机器学习方法计算大地热流具有一定的不确定性,参数特征的数量和精度等对计算结果有较大的影响。例如大陆岩石圈年龄在敏感性分析中可知其对热流贡献度相对较高,而数据精度较低,如果获得精度更高的该数据,则可计算得到相对更加准确的热流结果。此外从参数特征分析中可以看出,要获得更好的结果不应只着眼于提升训练数据的质量或者盲目增加训练特征的种类,而应考虑哪些特征以及有多少特征是值得信任和贡献度高的。

参考文献

Lerche I, Yarzab R F, Kendall C G.

Determination of Paleoheat flux from vitrinite reflectance data:REPLY

[J]. AAPG Bulletin, 1985, 68(11):1704-1717.

[本文引用: 1]

庞雄奇, 陈章明, 陈发景.

非线性变化古热流回剥模拟计算方法探讨

[J]. 大庆石油学院学报, 1994, 18(2):9-16.

[本文引用: 1]

Pang X Q, Chen Z M, Chen F J.

Discussion on the calculation method of nonlinear variation paleoheat flow stripping simulation

[J]. Journal of Daqing Petroleum Institute, 1994, 18(2):9-16.

[本文引用: 1]

魏东平, 石耀霖, 汤懋苍, 等.

利用气象地温资料反演大地热流

[J]. 地球物理学报, 1992, 35(6):733-739.

[本文引用: 1]

Wei D P, Shi Y L, Tang M C, et al.

Retrieving terrestrial heat flow from meteorological and geothermal data

[J]. Chinese Journal of Geophysics, 1992, 35(6):733-739.

[本文引用: 1]

董文杰, 汤懋苍.

用气象站地温资料计算多年平均土壤热流的初步结果

[J]. 高原气象, 1992, 11(2):115-125.

[本文引用: 1]

本文根据半无限空间的线性热传导理论, 利用我国288个气象台站1954-1989年0.8m, 3.2m的地温资料计算了土壤热流。初步结果表明:(1)如果气象台站的地温资料长于11年, 则滤波分析之后可用来计算平均的土壤热流(或地表热流);(2)本文与文献[4]给出的求导温度的方法精度相同;(3)以北京站为个例, 分析说明了地温梯度(T<sub>3.2</sub>T<sub>0.8</sub>), 年降水量和地震之间都有好的对应关系;(4)在绝大多数地区, 地表热流与深层大地热流的方向和量级都一致, 并且在如上两热流同时有计算值的区域, 它们的分布也很一致;(5)在沙漠地区, 地表热流与深层大地热流方向相反, 这表明在沙漠下面某一深度上有一"热汇层";(6)土壤热流的高值带与中国地震带的位置对应得非常好。

Dong W J, Tang M C.

Preliminary results of calculating multi-year average soil heat flow using ground temperature data from meteorological stations

[J]. Plateau Meteorology, 1992, 11(2):115-125.

[本文引用: 1]

Fox M C, Purucker M E, Olsen N.

Inferring magnetic crustal thickness and geothermal heat flux from crustal magnetic field models

[R]. Danish Meteorological Institute, 2009.

[本文引用: 1]

Martos Y M, Catalan M, Jordan T A, et al.

Heat flux distribution of Antarctica Unveiled

[J]. Geophysical Research Letters, 2017, 44(22):11417-11426.

DOI:10.1002/grl.v44.22      URL     [本文引用: 1]

唐晗晗, 郭良辉, 方圆.

青藏高原东南缘热流估算及与地震活动相关性分析

[J]. 地球物理学报, 2020, 63(3):1056-1069.

[本文引用: 1]

Tang H H, Guo L H, Fang Y.

Estimation of heat flow in the southeast margin of the Qinghai-Tibet Plateau and correlation analysis with seismic activity

[J]. Chinese Journal of Geophysics, 2020, 63(3):1056-1069.

[本文引用: 1]

Goutorbe B, Poort J, Lucazeau F, et al.

Global heat flow trends resolved from multiple geological and geophysical proxies

[J]. Geophysical Journal International, 2011, 187(3):1405-1419.

DOI:10.1111/j.1365-246X.2011.05228.x      URL     [本文引用: 1]

Rezvanbehbahani S, Stearns L A, Kadivar A, et al.

Predicting the geothermal heat flux in Greenland:A machine learning approach

[J]. Geophysical Research Letters, 2017, 44(24):12271-12279.

[本文引用: 1]

Lucazeau F.

Analysis and mapping of an updated terrestrial heat flow data set

[J]. Geochemistry,Geophysics,Geosystems, 2019, 20(8):4001-4024.

DOI:10.1029/2019GC008389      URL     [本文引用: 1]

Haklidir T.

Prediction of reservoir temperatures using hydrogeochemical data,Western Anatolia geothermal systems(Turkey):A machine learning approach

[J]. Natural Resources Research, 2020, 29(4):1-14.

DOI:10.1007/s11053-020-09627-1      [本文引用: 1]

Lösing M, Ebbing J.

Predicting geothermal heat flow in Antarctica with a machine learning approach

[J]. Journal of Geophysical Research:Solid Earth, 2021, 126(6):1-16.

[本文引用: 1]

刘卓. 基于变物性约束的重磁界面反演研究与应用[D]. 长春: 吉林大学, 2019.

[本文引用: 2]

Liu Z. Research and application of gravity and magnetic interface inversion based on variable physical property constraints[D]. Changchun: Jilin University, 2019.

[本文引用: 2]

刘子婧. 利用S波接收函数研究中国东北地区LAB深度[D]. 北京: 中国石油大学(北京), 2016.

[本文引用: 2]

Liu Z J. Using S-wave receiver function to study LAB depth in Northeast China[D]. Beijing: China University of Petroleum(Beijing), 2016.

[本文引用: 2]

王开燕, 刘丹, 柳俊茹, 等.

东北地区地壳结构研究

[J]. 地球物理学进展, 2015, 30(1):61-69.

[本文引用: 2]

Wang K Y, Liu D, Liu J R, et al.

Research on crustal structure in Northeast China

[J]. Progress in Geophysics, 2015, 30(1):61-69.

[本文引用: 2]

Samuel A.

Some studies in machine learning using the game of checkers

[J]. IBM Journal of Research and Development, 1959, 3(3):210-229.

DOI:10.1147/rd.33.0210      URL     [本文引用: 1]

Russell S, Norvig P.

Artificial intelligence:A modern approach,Third Edition

[J]. Artificial Intelligence, 2011, 175:935-937.

DOI:10.1016/j.artint.2011.01.005      URL     [本文引用: 1]

Fox Maule C, Purucker M E, Olsen N.

Inferring magnetic crustal thickness and geothermal heat flux from crustal magnetic field models

[R]. Danish Meteorological Institute, 2009.

[本文引用: 1]

Amante C, Eakins B W. ETOPO1 1 arc-minute global relief model:Procedures,data sources and analysis[M].National Oceanic and Atmospheric Administration Technical Memorandum,National Environmental Satellite,Data,and Information Service,National Geophysical Data Center, 2009.

[本文引用: 1]

Reguzzoni M, Sampietro D, Sansò F.

Global Moho from the combination of the CRUST2.0 model and GOCE data

[J]. Geophysical Journal International, 2013, 195:222-237.

DOI:10.1093/gji/ggt247      URL     [本文引用: 1]

Pasyanos M E, Masters T G, Laske G, et al.

LITHO1.0:An updated crust and lithospheric model of the Earth

[J]. Journal of Geophysical Research:Solid Earth, 2014, 119:2153-2173.

DOI:10.1002/jgrb.v119.3      URL     [本文引用: 1]

Poupinet G, Shapiro N M.

Worldwide distribution of ages of the continental lithosphere derived from a global seismic tomographic model

[J]. Lithos, 2009, 109(1):125-130.

DOI:10.1016/j.lithos.2008.10.023      URL     [本文引用: 1]

Balmino G, Vales N, Bonvalot S, et al.

Spherical harmonic modelling to ultra-high degree of Bouguer and isostatic anomalies

[J]. Journal of Geodesy, 2012, 86(7):499-520.

DOI:10.1007/s00190-011-0533-4      URL     [本文引用: 1]

Laske G, Masters G, Ma Z, et al.

Update on CRUST1.0 -A1-degree global model of Earth's crust

[J]. Geophysical Research Abstracts, 2013,15,2658.

[本文引用: 1]

Kaban M K, Schwintzer P, Reigber C.

A new isostatic model of the lithosphere and gravity field

[J]. Journal of Geodesy, 2004, 78(6):368-385.

DOI:10.1007/s00190-004-0401-6      URL     [本文引用: 1]

Maus S, Sazonova T, Hemant K, et al.

National geophysical data center candidate for the world digital magnetic anomaly map

[J]. Geochemistry,Geophysics,Geosystems, 2013, 8(6):1-10.

[本文引用: 1]

Bassin C.

The current limits of resolution for surface wave tomography in North America

[J]. Eos Transactions American Geophysical Union, 2000,81,F897.

[本文引用: 1]

USGS. Geologic province and thermo-tectonic age maps[M/OL]. https://earthquake.usgs.gov/data/crust/maps.php [2016-09-30].

URL     [本文引用: 1]

Shapiro N M, Ritzwoller M H.

Monte-Carlo inversion for a global shear-velocity model of the crust and uppermantle

[J]. Geophysical Journal International, 2002, 151(1):88-105.

DOI:10.1046/j.1365-246X.2002.01742.x      URL     [本文引用: 1]

Hartmann J, Moosdorf N.

The new global lithological map database GLiM:A representation of rock properties at the Earth surface

[J]. Geochemistry,Geophysics,Geosystems, 2012, 13(12):1-37.

DOI:10.1029/2011GC003955      URL     [本文引用: 1]

Coffin M F, Gahagan L M, Lawver L A.

Present-day plate boundary digital data compilation

[J]. University of Texas Institute for Geophysics Technical Report, 1998,174,5.

[本文引用: 1]

Shapiro N M, Ritzwoller M H.

Inferring surface heat flux distributions guided by a global seismic model:Particular application to Antarctica

[J]. Earth and Planetary Science Letters, 2004, 223(1):213-224.

DOI:10.1016/j.epsl.2004.04.011      URL     [本文引用: 1]

Gosnold W. The global heat flow database[M/OL]. http://www.heatflow.und.ed-u/index2.html [2016-09-30].

URL     [本文引用: 3]

吴乾蕃.

松辽盆地地热场

[J]. 地震研究, 1991, 14(1):31-40.

[本文引用: 1]

Wu Q F.

Geothermal field in Songliao basin

[J]. Earthquake Research, 1991, 14(1):31-40.

[本文引用: 1]

姜光政, 高堋, 饶松, 等.

中国大陆地区大地热流数据汇编(第四版)

[J]. 地球物理学报, 2016, 59(8):2892-2910.

[本文引用: 1]

Jiang G Z, Gao P, Rao S, et al.

Compilation of earth heat flow data in Chinese Mainland(Fourth Edition)

[J]. Chinese Journal of Geophysics, 2016, 59(8):2892-2910.

[本文引用: 1]

刘耀光.

松辽盆地地热场特征与油气勘探的关系

[J]. 石油勘探与开发, 1982(3):26-31.

[本文引用: 3]

Liu Y G.

Relationship between geothermal field characteristics and oil and gas exploration in Songliao Basin

[J]. Petroleum Exploration and Development, 1982(3):26-31.

[本文引用: 3]

He C S, Dong S W, Chen X H, et al.

Seismic evidence for plume-induced rifting in the Songliao Basin of Northeast China

[J]. Tectonophysics, 2014, 627:171-181.

DOI:10.1016/j.tecto.2013.07.015      URL     [本文引用: 1]

肖龙, 王方正, 王华, 等.

地幔柱构造对松辽盆地及渤海湾盆地形成的制约

[J]. 地球科学——中国地质大学学报, 2004, 29(3):283-292.

[本文引用: 1]

Xiao L, Wang F Z, Wang H, et al.

Constraints of mantle plume structure on the formation of Songliao basin and Bohai Bay basin

[J]. Earth Science-Journal of China University of Geosciences, 2004, 29(3):283-292.

[本文引用: 1]

张尔华, 姜传金, 张元高, 等.

徐家围子断陷深层结构形成与演化的探讨

[J]. 岩石学报, 2010, 26(1):149-157.

[本文引用: 1]

Zhang E H, Jiang C J, Zhang Y G, et al.

Discussion on the formation and evolution of deep structure of Xujiaweizi fault depression

[J]. Journal of Rock, 2010, 26(1):149-157.

[本文引用: 1]

Sobolo I M.

Sensitivity estimates for nonlinear mathematical models

[J]. Math. Model. Comput. Exp., 1993, 1(4):407-417.

[本文引用: 1]

Sobolo I M.

Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates

[J]. Math. Comput. Simul., 2001, 55:271-280.

DOI:10.1016/S0378-4754(00)00270-6      URL     [本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com