一种适用于地磁梯度匹配导航的ISCCP算法

doi:10.11720/wtyht.2022.1567

一种适用于地磁梯度匹配导航的ISCCP算法

金子翔^,¹, 许苏鹏¹, 张贵宾^,¹, 梁建¹, 董根旺², 范振宇¹

1.中国地质大学(北京) 地球物理与信息技术学院,北京 100083

2.中国冶金地质总局地球物理勘查院,河北保定 071051

An ISCCP algorithm for geomagnetic gradient matching for navigation

JIN Zi-Xiang^,¹, XU Su-Peng¹, ZHANG Gui-Bin^,¹, LIANG Jian¹, Dong Gen-Wang², FAN Zhen-Yu¹

1. School of Geophysics and Information Technology, China University of Geosciences(Beijing), Beijing 100083, China

2. Geophysical Exploration Academy of China Metallurgical Geology Bureau, Baoding 071051, China

通讯作者: 张贵宾(1958-),男,教授,博士生导师,主要从事地球物理数据处理和反演等研究工作。Email:gbzhang@cugb.edu.cn

责任编辑: 王萌

收稿日期: 2021-10-19 修回日期: 2022-01-24

基金资助:

中国电波传播研究所稳定支持科研项目(A132007W06)
中国地质调查局项目“全国陆域及海区地质图件更新与共享”(DD20190370)

Received: 2021-10-19 Revised: 2022-01-24

作者简介 About authors

金子翔(1995-),男,硕士研究生,主要从事地球物理/惯性组合导航算法研究工作。Email:jin_zixiang@163.com

摘要

针对迭代最近等值线点(ICCP)算法在地磁变化平缓的区域匹配误差大,甚至出现误匹配的问题,本文首先建立ICCP算法的误差模型,阐明ICCP算法在这些区域匹配误差大的原因,并基于该误差模型,提出适用于地磁梯度匹配导航的迭代搜索最近等值线点(ISCCP)算法,该算法在ICCP的基础上改进了最近点搜索方式,利用地磁3个正交方向梯度信息进行迭代搜索。最后通过仿真实验表明,ISCCP算法平均点位误差能控制在半个网格长度以内,精度相较于ICCP算法提高了约15倍,有效解决了ICCP算法在地磁变化平缓的区域匹配误差大的问题。

关键词： 地磁梯度匹配导航; ICCP算法; 误差模型; 迭代搜索

Abstract

The iterated closest contour point (ICCP) algorithm results in large matching errors and even false matching in areas with small geomagnetic variations. Given this, this study established an error model for the ICCP algorithm in order to determine the causes of the large matching errors in the areas. Based on this model, this study proposed an iterated search closest contour point (ISCCP) algorithm suitable for geomagnetic gradient matching for navigation. In the proposed algorithm, the closest point search method was improved based on the ICCP, and an iterative search was performed using the geomagnetic gradient information of three orthogonal directions. The simulation results show that the average point error of the ISCCP algorithm can be controlled within half a grid length, with a precision about 15 times higher than that of the ICCP algorithm. Therefore, the ISCCP algorithm proposed in this study can effectively eliminate the large matching errors in areas with small geomagnetic variations caused by the ICCP algorithm.

Keywords： geomagnetic gradient matching navigation; ICCP algorithm; error model; iterative search

PDF (3873KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

金子翔, 许苏鹏, 张贵宾, 梁建, 董根旺, 范振宇. 一种适用于地磁梯度匹配导航的ISCCP算法[J]. 物探与化探, 2022, 46(5): 1225-1231 doi:10.11720/wtyht.2022.1567

JIN Zi-Xiang, XU Su-Peng, ZHANG Gui-Bin, LIANG Jian, Dong Gen-Wang, FAN Zhen-Yu. An ISCCP algorithm for geomagnetic gradient matching for navigation[J]. Geophysical and Geochemical Exploration, 2022, 46(5): 1225-1231 doi:10.11720/wtyht.2022.1567

0 引言

自主导航是实现国防战略的关键技术,地磁匹配导航作为惯性导航系统(inertia navigation system,INS)的一种重要辅助手段,利用其不依靠外界信号源,不向外界辐射能量,不受地点、气候等外界条件限制,隐蔽性好等特点,能完成航行器在水下长航距、长航时导航,实现真正的无源导航^[1⇓-3]。

由于地磁匹配算法的导航精度与匹配区域的地磁变化程度密切相关,所以在一些地磁变化平缓的区域,轮廓匹配(contour matching,CM)和迭代最近等值线点(iterated closest contour point,ICCP)算法等一维算法的匹配精度较低,甚至会出现误匹配的情况^[4-5],为此,研究人员提出不少解决方案,大致可分为两类。

第一类解决方案为搜索合适的匹配区域或匹配路径,Sun等^[6]采用免疫粒子群优化算法在地磁参考图中智能地选择最佳匹配区域,且在该区域内使用均方偏差和归一化乘积算法的相关匹配算法能得到更高的匹配精度。Xu等^[7]通过采用启发式和随机搜索算法的地磁场导航路径规划方法,可以有效地避免非匹配导航区域,并在水下地磁匹配导航应用中实现有效的路径规划功能。虽然这类解决方案能够有效地提高匹配精度,但是降低了航行器的机动性。

随着三轴磁传感器的发展和地磁测量技术的进步^[8-9],出现了第二类解决方案,即利用多维地磁信息进行地磁匹配导航。Song等^[10]提出了一种利用地磁矢量的地磁匹配导航方法,该方法在匹配区域地磁熵信息较小或地磁等值线变化不明显的情况下,仍能大大提高匹配概率和定位精度,且在实际地磁参考图的仿真中验证了该算法的有效性。Chen等^[11]将可信点集和航迹搜索原理与地磁矢量相关约束匹配原理相结合,提出了一种基于矢量匹配算法的地磁匹配导航新方法。通过仿真和实验分析了匹配和校正方法的性能。王琼等^[12]利用地磁场的矢量性提出一种基于遗传算法的地磁匹配搜索方法,仿真结果证明该方法在地磁场平缓区域定位的有效性,同时具有较好的定位精度。利用地磁矢量导航虽然能够有效提供匹配精度,但同时也容易受到地磁日变的影响。

本文提出一种适用于地磁梯度匹配导航的迭代搜索最近等值线点(iterated search closest contour point,ISCCP)算法,一方面,将地磁3个正交方向的梯度数据应用于匹配导航,能有效降低地磁日变给匹配精度带来的影响,且地磁梯度信息相较于地磁总场可利用的特征更加丰富^[13]。另一方面,针对ICCP算法在地磁变化缓慢的区域匹配精度差的问题,该算法在ICCP误差分析基础上,改进了ICCP的搜索方式,即利用迭代法多次迭代搜索最近等值线点。经理论分析与仿真实验,ISCCP算法能够有效提高ICCP算法在地磁变化平缓区域的匹配精度,且具有较好的实时性。

1 ICCP误差模型

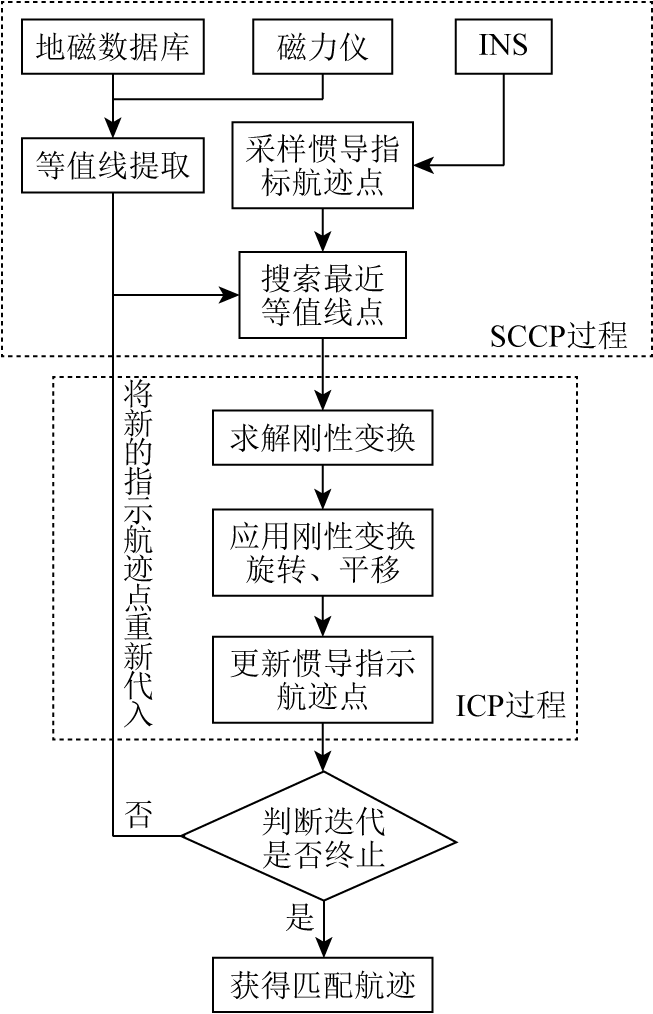
ICCP算法过程如图1所示,主要为搜索最近等值线点(search closest contour point,SCCP)与迭代最近点(iterative closest point,ICP)两个过程。首先在SCCP过程中,利用航行器在导航过程中测量的地磁值在地磁数据库中提取等值线,并在等值线上搜索与惯导指示航迹点最近的点^[14-15],该点即为最近等值线点(closest contour point,CCP)。其次进行ICP过程,该过程作用是将惯导的指示航迹点通过刚性变换中的旋转与平移变换尽可能地逼近CCP。最后,判断本次匹配结果与上次匹配结果是否在一个阈值范围内,若是则判断为收敛,否则将本次匹配的结果代入SCCP过程中重新进行匹配^[16-17]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 ICCP匹配流程

Fig.1 ICCP matching process

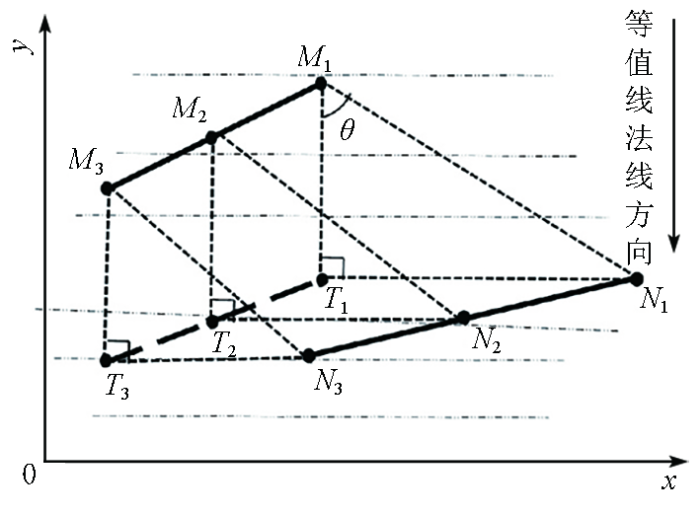
由此过程可知,SCCP作为ICCP算法的第1个步骤,决定整个算法的精度。为研究SCCP对ICCP算法精度的影响,如图2,取地磁变化缓慢区域中一段匹配路径进行分析。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 ICCP误差分析

Fig.2 ICCP error analysis

惯导指示航迹为 $M_{i} (i = 1,2, 3)$ ,航行器实际航迹为 $N_{i} (i = 1,2, 3)$ 。惯性指示航迹的点位误差 $e$ 为

(1)

e = \overset{n}{\sum_{i = 1}} ‖ \vec{M_{i} N_{i}} ‖

其中: $\vec{M_{i} N_{i}}$ 为惯导航迹点与实际航迹点之间的误差向量。

进行SCCP过程时,根据实际航迹点 $N_{i}$ 所测量的地磁值在地磁数据库找到地磁等值线,并在这些等值线上寻找一组点集 $T_{i} (i = 1,2, 3)$ ,使得惯导指示航迹 $M_{i}$ 到该点集的距离最近,即满足下列条件

(2)

\vec{M_{i} T_{i}} ⊥ \vec{T_{i} N_{i}}

则图2中 $T_{i}$ 即为所求的CCP。然后利用ICP将惯导指示航迹 $M_{i}$ 变换到 $T_{i}$ 上,并且重复SCCP与ICP直至收敛。由于每次SCCP过程中CCP都为 $T_{i}$ ,所以最终的匹配结果即为 $T_{i}$ ,陷入局部最优解,且匹配的误差 $e_{m}$ 为

(3)

e_{m} = \overset{n}{\sum_{i = 1}} ‖ \vec{T_{i} N_{i}} ‖

其中: $\vec{T_{i} N_{i}}$ 为匹配结果点与实际航迹点之间的误差向量。

设惯导的误差向量 $\vec{M_{i} N_{i}}$ 与等值线法线方向的夹角为 $θ$ ,得到ICCP匹配误差模型为

(4)

e_{m} = s i n θ \times \overset{n}{\sum_{i = 1}} ‖ \vec{M_{i} N_{i}} ‖

将式(1)代入得

(5)

e_{m} = s i n θ \times e

。

由该式结合上述推导可知:

1)当惯导误差向量 $\vec{M_{i} N_{i}}$ 与等值线法线方向的夹角 $θ$ 越大,匹配结果的误差越大;当 $θ = 0 °$ ,即两者平行时, $M_{i}$ 到等值线的最短距离与 $\vec{M_{i} N_{i}}$ 重合,则实际航迹点 $N_{i}$ 即为所求的CCP,此时再利用ICP匹配能得到较好的匹配结果;当 $θ = 90 °$ ,即两者垂直时, $M_{i}$ 与 $N_{i}$ 位于同一等值线上,则惯导指示航迹点 $M_{i}$ 为所求的CCP,导致匹配误差 $e_{m} = e$ 。

2)惯导的误差向量 $\vec{M_{i} N_{i}}$ 可分解为沿等值线法线方向的误差向量 $\vec{M_{i} T_{i}}$ 以及沿等值线切线方向的误差向量 $\vec{T_{i} N_{i}}$ ,利用ICCP算法则能够有效减少误差向量 $\vec{M_{i} T_{i}}$ ,但是无法减少误差向量 $\vec{T_{i} N_{i}}$ 。

综上所述,在地磁变化缓慢的区域,ICCP算法只能有效减少沿等值线法线方向的惯导误差,但是无法减少沿等值线切线方向的误差。需要注意的是,以上分析建立在理想模型上,由于实际匹配区域中所有的地磁等值线的切线方向并不完全一致,导致搜索到的CCP与上述结果具有偏差,此时利用ICP算法中的欧式距离最小原则,将带误差的惯导指示点通过变换尽可能地逼近CCP。

2 ISCCP算法原理

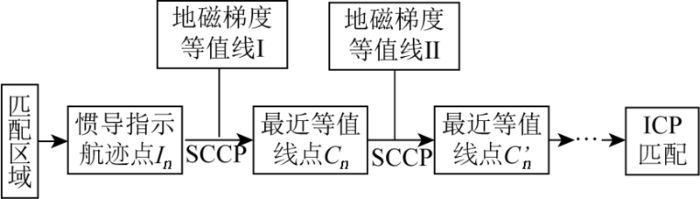
根据前面的分析,ICCP算法的匹配精度与地磁等值线的分布密切相关,且误差主要来源于SCCP的过程,所以为搜索到最佳的CCP以提高匹配精度,本文提出ISCCP算法,该算法对ICCP中的SCCP过程进行改进,如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 ISCCP匹配流程

Fig.3 ISCCP matching process

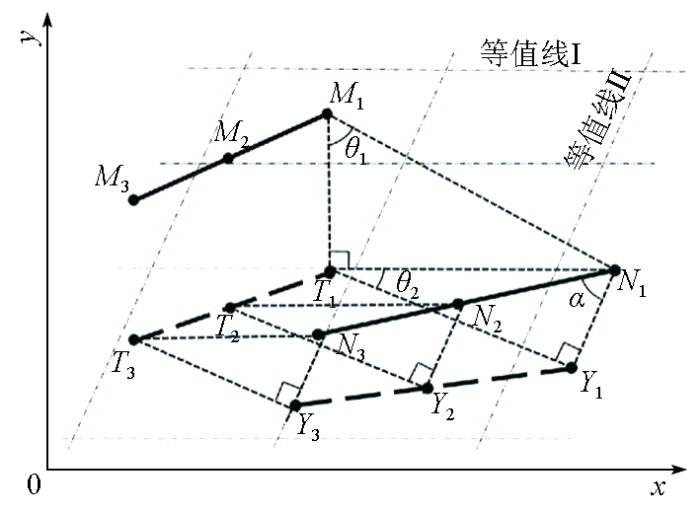
该过程利用地磁3个正交方向的梯度等值线信息,并采用迭代搜索的方式,进行多次SCCP过程迭代实现CCP逼近实际航迹点,具体原理如图4。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 ISCCP误差分析

Fig.4 ISCCP error analysis

由于地磁梯度有3个正交方向的等值线信息,因此我们在图2的基础上增加了等值线Ⅱ,如图4所示。由上节推导过程可知第一次SCCP为 $T_{i}$ ,与实际航迹点 $N_{i}$ 的误差为

(6)

e_{1} = \overset{n}{\sum_{i = 1}} ‖ \vec{T_{i} N_{i}} ‖ = \overset{n}{\sum_{i = 1}} ‖ \vec{M_{i} N_{i}} ‖ \times s i n θ_{1}

式中: $\vec{T_{i} N_{i}}$ 为第一次SCCP的误差向量; $\vec{M_{i} N_{i}}$ 为惯导指示航迹点误差向量。

第二次SCCP以上次搜索结果 $T_{i}$ 作为本次搜索的起点进行迭代,经过在等值线Ⅱ中SCCP的过程,得CCP为 $Y_{i}$ ,则第二次搜索的结果误差 $e_{2}$ 为

(7)

e_{2} = \overset{n}{\sum_{i = 1}} ‖ \vec{Y_{i} N_{i}} ‖

其中: $\vec{Y_{i} N_{i}}$ 为第二次SCCP的误差向量。

设等值线Ⅱ与等值线Ⅰ的夹角为 $α$ ,得到下式

(8)

e_{2} = \overset{n}{\sum_{i = 1}} ‖ \vec{T_{i} N_{i}} ‖ \times c o s α

将式(6)代入,得

(9)

e_{2} = e_{1} \times c o s α

由该式可知:当等值线Ⅰ固定时, $θ_{1}$ 不变, $e_{1}$ 也不变,随着等值线Ⅱ与等值线Ⅰ的夹角 $α$ 越大,搜索的CCP的误差越小;当 $α = 0 °$ 时,即等值线相互平行时,等值线Ⅱ的法线方向与第一次搜索的误差矢量 $\vec{T_{1} N_{1}}$ 相互垂直,根据上节结论,CCP为 $T_{i}$ ,此时进行ICP匹配误差最大;当 $α = 90 °$ 时,即等值线相互垂直时,等值线Ⅱ的法线方向与第一次搜索的误差矢量 $\vec{T_{1} N_{1}}$ 相互平行,根据上节结论,实际航迹点 $N_{i}$ 即为所求的CCP,此时进行ICP匹配精度最高。

以上论证表明,当匹配区域中有相互垂直的等值线时,利用这些等值线迭代SCCP过程中,能够快速找到实际航迹点的位置,并通过ICP算法将惯导指示航迹点逼近实际航迹点。

由于实际匹配区域中,相互垂直的地磁梯度等值线信息较少,为确保地磁匹配导航的精度,利用迭代法对所有的地磁梯度等值线信息进行SCCP也能有效减少惯导指示航迹点的误差。证明如下:

将式(1)、式(6)代入式(7),得

(10)

e_{2} = e \times s i n θ_{1} \times c o s α

设 $θ_{2}$ 为第1次SCCP的误差矢量 $\vec{T_{1} N_{1}}$ 与等值线Ⅱ法线方向的夹角,根据图4,可得

(11)

α = 90 ° - θ_{2}

即

(12)

e_{2} = e \times s i n θ_{1} \times s i n θ_{2}

。

若有等值线Ⅲ,且其法线方向与第2次SCCP的误差向量 $\vec{Y_{1} N_{1}}$ 夹角为 $θ_{3}$ ,则第3次搜索SCCP的误差为

(13)

e_{3} = e \times s i n θ_{1} \times s i n θ_{2} \times s i n θ_{3}

依次类推,直至等值线 $n$ ,且该等值线的法线方向与上一次SCCP的误差向量夹角为 $θ_{n}$ ,那么本次SCCP的误差 $e_{n}$ 即为

(14)

e_{n} = e_{n - 1} \times s i n θ_{n}

其中: $e_{n - 1}$ 为上一次SCCP的误差,且 $0 \leq θ_{n} \leq 90 °$ 。

由此可知, $e_{n} \leq e_{n - 1}$ ,则每次迭代SCCP都可以有效减少CCP与实际航迹点之间的误差。

综上所述,在进行ISCCP算法匹配时,首先判断匹配的区域是否有相互垂直的地磁梯度等值线,若有,只选择相互垂直的地磁梯度等值线进行ISCCP,否则对所有的地磁梯度等值线进行ISCCP。

3 仿真实验

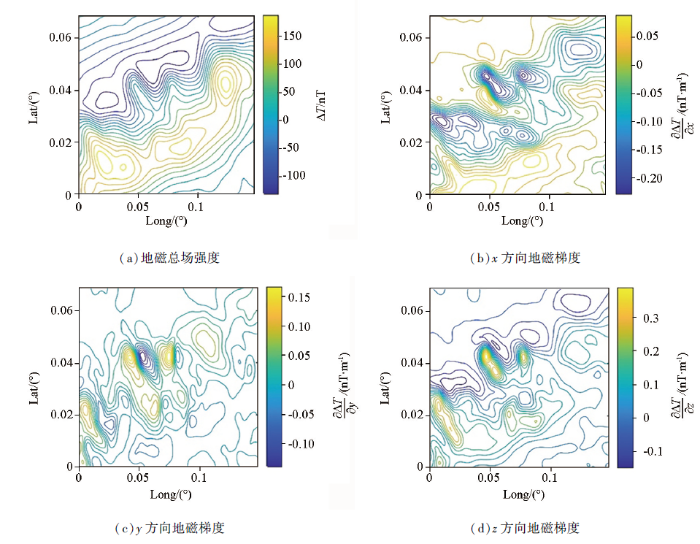
为了验证ISCCP算法的有效性,进行仿真实验前,首先利用克里金插值模型对实测航磁3个正交方向的梯度数据网格化,作为匹配算法所用的背景场,网格间距为100 m×100 m,如图5所示。之后在背景场中加入2%的高斯白噪声作为导航过程中测量的地磁梯度数据来源;其次,设计航行器的实际航行轨迹获取姿态、速度与位置信息,然后利用捷联惯导解算的反演算法逆推出惯性元件的导航信息,包括角增量与速度增量,接着再加入各项惯导系统误差,通过捷联惯导解算得到带有误差的惯导指示航迹^[18],表1给出了惯导系统误差参数;最后,将以上数据代入匹配算法中进行计算,其中,ICCP算法利用地磁总场数据进行导航,ISCCP利用地磁梯度数据进行导航,匹配参数如表1所示。为验证之前得出的结论,分别进行直线航迹与曲线航迹的仿真实验。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 地磁总场与地磁梯度

Fig.5 Total geomagnetic field and geomagnetic gradient

表1 仿真参数

Table 1 Simulation parameters

	参数描述	参数值
惯导系统误差	陀螺常值偏零	0.5 °/h
	角度随机游走	0.01 °/ $\sqrt{h}$
	加速度常值偏值	150 μg
	速度随机游走	10 μg/ $\sqrt{H z}$
匹配过程	航行速度	10 m·s^-1
	采样点数	72
	每次匹配点数	3
	采样点间隔时间	8 s
	初始惯导误差	100 m

新窗口打开| 下载CSV

3.1 直线航迹仿真

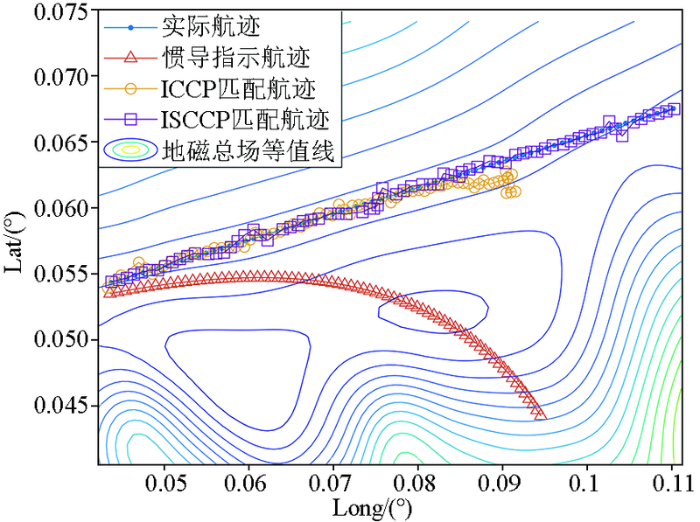
直线航迹仿真如图6所示,ICCP算法在前一段的航迹匹配结果较好,总体匹配航迹的航向基本与实际航迹一致。根据之前的结论,这是由于该算法只能减小沿等值线法向方向的误差,但同时沿等值线切线方向的误差随时间积累越来越大,导致航程的偏差越来越大。而ISCCP算法通过3个正交方向丰富的地磁梯度信息能较好约束惯导误差,且仅需要3个采样点进行匹配就能取得不错的匹配效果。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 直线航迹匹配结果

Fig.6 Linear track matching results

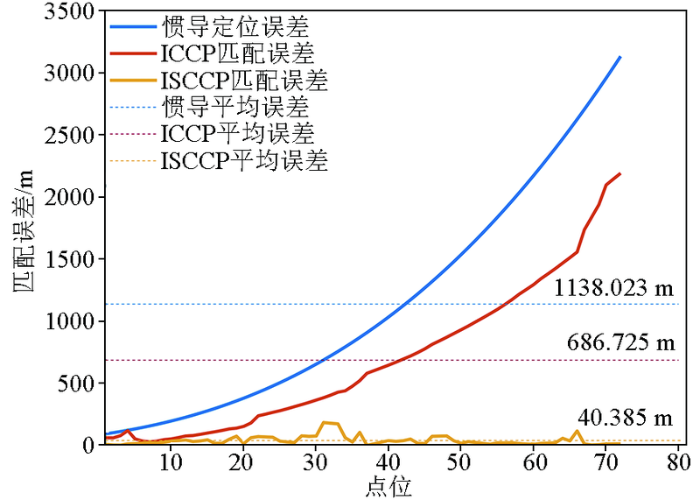
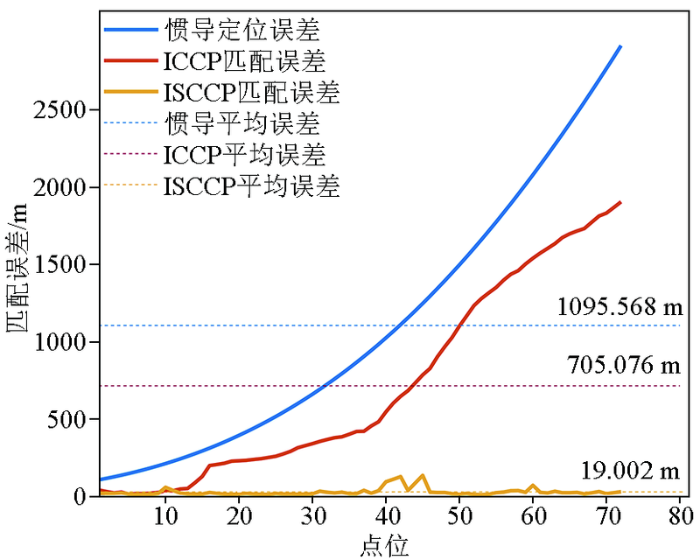
匹配误差如图7所示,直线航迹下ISCCP算法的最大点位误差为184.550 m,最小点位误差仅为1.772 m,平均点位误差为40.385 m,能将误差控制在半个网格长度内。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 直线航迹匹配误差

Fig.7 Linear track matching error

3.2 曲线航迹仿真

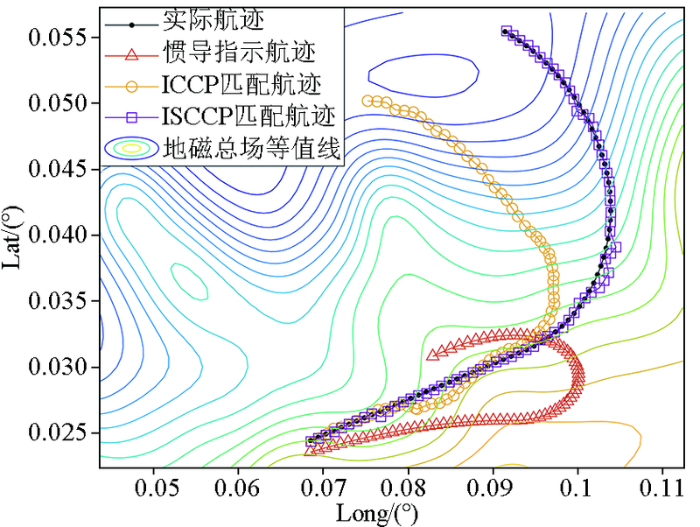
曲线航迹由图8所示,ICCP算法在前一段的匹配效果较好,总体匹配航迹的航程与实际航迹大致相同。但之后航迹的航向逐渐偏离实际航迹,这也是由于算法只能减小沿等值线法向方向的误差,导致沿等值线切线方向的误差不能及时减小,总体误差越来越大,而ISCCP算法也还能保持较高的精度。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 曲线航迹匹配情况

Fig.8 Curve track matching results

如图9所示,曲线航迹下ISCCP算法的最大点位误差为125.701 m,最小点位误差仅为0.645 m,平均点位误差为19.002 m,误差也在半个网格长度内。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 曲线航迹匹配误差

Fig.9 Curve track matching error

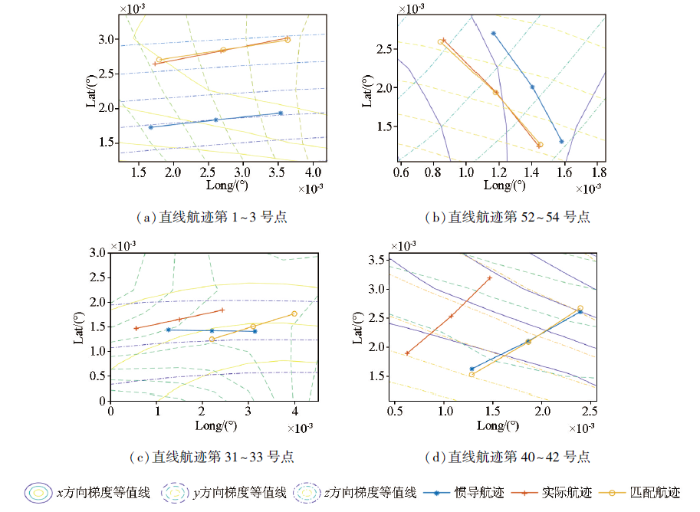
通过3.1与3.2的仿真实验表明,ICCP算法采用单一信息量进行导航时,其原理上固有的局限性导致该算法在上述情形时匹配精度低,ISCCP利用地磁梯度的3个正交方向的信息进行匹配导航的同时,采用迭代的搜索方式能最大程度上减小惯导误差。需要注意的是,ISCCP匹配精度也是受地磁梯度等值线分布的影响,如直线航迹的第31~33号点,曲线航迹的第40~42号点匹配误差最大,直线航迹的第1~3号点,曲线航迹的第52~54号点匹配误差较小。下面对这4种情况进行分析。

3.3 仿真分析

由图10所示,当匹配区域中的地磁梯度等值线相交,且接近垂直时,ISCCP算法匹配的效果最好,当匹配区域中的等值线接近平行时,相当于用单一地磁信息进行匹配导航,匹配的效果自然也差,这也验证了之前的结论。因此,利用地磁丰富的3个正交方向梯度信息使等值线出现接近垂直的机率更高,能有效提高ISCCP算法的精度,如若需要进一步提高算法的精度,可以优先选取地磁梯度等值线近似相互垂直的区域进行匹配。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 局部匹配结果

Fig.10 Local matching results

4 结论

本文首先阐明ICCP算法在地磁变化缓慢的区域匹配误差大的原因,即ICCP算法只能减少沿等值线法线方向的误差,无法有效减少沿等值线切线方向的误差;其次,本文提出了适用于地磁梯度匹配导航的ISCCP算法,经过误差模型分析,当匹配区域中有相互垂直的地磁梯度等值线时,利用ISCCP算法能够快速准确找到实际航迹点的位置,当匹配区域没有相互垂直的地磁梯度等值线时,利用迭代法对所有的等值线进行ISCCP也能有效减少惯导指示航迹点的误差;最后,经仿真实验表明,ISCCP算法在地磁变化平缓的区域匹配时,平均点位误差能控制在半个网格长度以内,有效提高了ICCP算法在地磁变化平缓的区域匹配时的精度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

陈国雄, 刘天佑, 冯杰.

考虑日变影响的小尺度地磁无源导航方法

[J]. 物探与化探, 2010, 34(5):590-594.