|
|
|
| Application of least-squares collocation to the gridding of magnetic anomaly data |
GAO Xiao-Wei1( ), LI Xiong-Wei1, PANG Shao-Dong1, LI Wen-Gang1, YAO Wei-Hua1, DU Jin-Song2,3( ), LI Xiong-Wei1, PANG Shao-Dong1, LI Wen-Gang1, YAO Wei-Hua1, DU Jin-Song2,3( ) ) |
1. CCTEG Xi'an Research Institute (Group) Co., Ltd., Xi'an 710077, China
2. Hubei Subsurface Multi-scale Imaging Key Laboratory, School of Geophysics and Geomatics, China University of Geosciences (Wuhan), Wuhan 430074, China
3. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences (Wuhan), Wuhan 430074, China |
|
|
|
|
Abstract Traditional gridding methods struggle to balance computational accuracy and efficiency when processing irregularly distributed magnetic anomaly data. To address this issue, this study applied the classic least-squares collocation method from geodesy to the gridding of ground-based magnetic anomaly data. This application was verified through the test and analysis of the simulation data and the actual coalfield data. The results indicate that the computational accuracy of gridding based on least-squares collocation is dictated by the error estimation of discrete observational data and the selection and fitting of the covariance function. More accurate error estimation contributes to higher-accuracy interpolation. A polynomial function is a simple and effective empirical covariance function for processing magnetic anomaly data. The least-squares collocation method demonstrates more effective noise suppression compared to the Kriging, minimum curvature, and radial basis function methods. Overall, applying the least-squares collocation to the gridding of magnetic anomaly data can enhance the accuracy and efficiency of data processing.
|
|
Received: 10 July 2024
Published: 22 April 2025
|
|
|
|
|
|

|
Simulated theoretical data (a) and observation data (b)
|
|
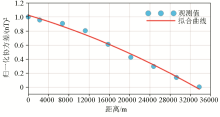
Calculated covariance values and fitted covariance function
|

|
Predicted data (a) and interpolation errors (b)
|

|
Simulated theoretical data (a), noises (b) and practical observation data (c)
(black dots represent synthetic observation locations)
|

输入的噪声
标准差 | 残差均方根 | 平均残差 | 最大残差 | 最小残差 | | ±0 | ±8.879 0 | 1.129 5 | 40.800 0 | -24.370 0 | | ±10 | ±7.338 3 | 0.074 9 | 35.390 0 | -33.490 0 | | ±20 | ±8.854 2 | 1.126 9 | 41.260 0 | -24.810 0 |
|
Statistic parameters of calculation accuracy in cases of setting different levels of data noisesnT
|
|
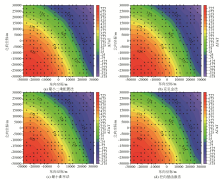
Calculating results by using different interpolation methods
|
|
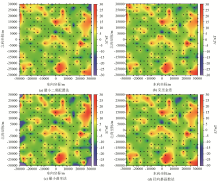
Differences between calculating results and theoretical data by using different interpolation methods
|

| 网格化方法 | 残差均方根 | 平均残差 | 最大残差 | 最小残差 | | 最小二乘配置法 | ±8.559 2 | 1.594 3 | 30.940 0 | -32.890 0 | | 克里金法 | ±8.676 2 | 1.698 3 | 36.110 0 | -20.990 0 | | 最小曲率法 | ±19.212 9 | -0.671 3 | 123.100 0 | -218.300 0 | | 径向基函数法 | ±8.996 6 | 1.714 8 | 32.970 0 | -20.990 0 |
|
Statistic parameters of calculating accuracy of four interpolation methodsnT
|

|
Columnar statistical charts of residual data by using different interpolation methods
|
|
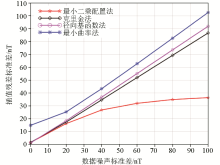
Standard deviation values of calculating residuals in cases of different noise levels by using different interpolation methods
|

|
Elevation (a), original (b) and interference removed (c) ΔT magnetic anomaly data
|
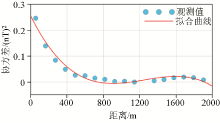
|
Calculated covariance values and fitted covariance function curve by practical observation data
|

|
Calculated grid results by using different interpolation methods
|

|
Differences between calculated results and practical data by using different interpolation methods
|

| 网格化方法 | 均方根值 | 平均值 | 最大值 | 最小值 | | 最小二乘配置法 | ±29.465 4 | -0.018 0 | 1.175 4×10+03 | -1.496 4×10+03 | | 克里金法 | ±44.854 6 | -2.791 2 | 1.539 3×10+03 | -2.362 1×10+03 | | 最小曲率法 | ±62.034 4 | 0.044 3 | 1.826 9×10+03 | -2.462 5×10+03 | | 径向基函数法 | ±55.273 6 | 0.679 2 | 1.844 4×10+03 | -2.508 2×10+03 |
|
Statistic parameters of calculating error of four gridding methodsnT
|

|
Columnar statistical charts of calculating errors by different gridding methods
|
| [1] |
郭良辉, 孟小红, 郭志宏, 等. 地球物理不规则分布数据的空间网格化法[J]. 物探与化探, 2005, 29(5):438-442.
|
| [1] |
Guo L H, Meng X H, Guo Z H, et al. Gridding methods of geophysical irregular data in space domain[J]. Geophysical and Geochemical Exploration, 2005, 29(5):438-442.
|
| [2] |
陈欢欢, 李星, 丁文秀. Surfer 8.0等值线绘制中的十二种插值方法[J]. 工程地球物理学报, 2007, 4(1):52-57.
|
| [2] |
Chen H H, Li X, Ding W X. Twelve kinds of gridding methods of surfer 8.0 in isoline drawing[J]. Chinese Journal of Engineering Geophysics, 2007, 4(1):52-57.
|
| [3] |
刘兆平, 杨进, 武炜. 地球物理数据网格化方法的选取[J]. 物探与化探, 2010, 34(1):93-97.
|
| [3] |
Liu Z P, Yang J, Wu W. The choice of gridding methods for geophysical data[J]. Geophysical and Geochemical Exploration, 2010, 34(1):93-97.
|
| [4] |
李小东, 金胜, 王阳玲, 等. 散乱离散点数据的三角形网格化快速成图[J]. 物探与化探, 2015, 39(1):156-160.
|
| [4] |
Li X D, Jin S, Wang Y L, et al. Triangular grid-based rapid mapping of scattered data[J]. Geophysical and Geochemical Exploration, 2015, 39(1):156-160.
|
| [5] |
孟小红, 侯建全, 梁宏英, 等. 离散光滑插值方法在地球物理位场中的快速实现[J]. 物探与化探, 2002, 26(4):302-306.
|
| [5] |
Meng X H, Hou J Q, Liang H Y, et al. The fast realization of discrete smooth interpolation in the interpolation of potential data[J]. Geophysical and Geochemical Exploration, 2002, 26(4):302-306.
|
| [6] |
郭志宏. 一种实用的等值线型数据网格化方法[J]. 物探与化探, 2001, 25(3):203-208.
|
| [6] |
Guo Z H. A practical contour type data gridding technique[J]. Geophysical and Geochemical Exploration, 2001, 25(3):203-208.
|
| [7] |
闫永利, 陈本池, 周凤桐. 提高航空物探网格化精度的一种方法[J]. 物探与化探, 1997, 21(2):81-90.
|
| [7] |
Yan Y L, Chen B C, Zhou F T. A method for improving gridded precision of airborne geophysical survey[J]. Geophysical and Geochemical Exploration, 1997, 21(2):81-90.
|
| [8] |
张冕, 张春灌, 赵敏, 等. 地球磁异常EMAG2v3与全球重力数据库V29数据质量综合评估——以北极地区Aegir脊为例[J]. 物探与化探, 2023, 47(6):1410-1416.
|
| [8] |
Zhang M, Zhang C G, Zhao M, et al. An integrated data quality evaluation of Earth magnetic anomaly grid EMAG2v3 and global gravimetric database V29:A case study of the Aegir ridge in the Arctic[J]. Geophysical and Geochemical Exploration, 2023, 47(6):1410-1416.
|
| [9] |
Matheron G. Principles of geostatistics[J]. Economic Geology, 1963, 58(8):1246-1266.
|
| [10] |
孙洪泉. 地质统计学及其应用[M]. 徐州: 中国矿业大学出版社, 1990.
|
| [10] |
Sun H Q. Geostatistics and its application[M]. Xuzhou: University of Mining & Technology Press, 1990.
|
| [11] |
Hansen R O. Interpretive gridding by anisotropic Kriging[J]. Geophysics, 1993, 58(10):1491-1497.
|
| [12] |
彭泽辉, 李辉, 申重阳, 等. 基于最小二乘配置的重力变化插值方法[J]. 大地测量与地球动力学, 2010, 30(3):43-46.
|
| [12] |
Peng Z H, Li H, Shen C Y, et al. Interpolation method based on least squares collocation for dynamic gravity changes[J]. Journal of Geodesy and Geodynamics, 2010, 30(3):43-46.
|
| [13] |
阮明明, 陈石, 韩建成. 用最小二乘配置法构建局部重力场模型[J]. 地震学报, 2020, 42(1):53-65,120.
|
| [13] |
Ruan M M, Chen S, Han J C. Regional gravity field model constructed by the least squares collocation[J]. Acta Seismologica Sinica, 2020, 42(1):53-65,120.
|
| [14] |
Briggs I C. Machine contouring using minimum curvature[J]. Geophysics, 1974, 39(1):39-48.
|
| [15] |
Smith W H F, Wessel P. Gridding with continuous curvature splines in tension[J]. Geophysics, 1990, 55(3):293-305.
|
| [16] |
许海红, 韩小锋, 袁炳强, 等. 基于径向基函数的1:5万规则分布重力数据插值参数优选[J]. 物探与化探, 2021, 45(6):1539-1552.
|
| [16] |
Xu H H, Han X F, Yuan B Q, et al. Optimization of interpolation parameters for 1:50,000 regular distribution gravity data based on radial basis function[J]. Geophysical and Geochemical Exploration, 2021, 45(6):1539-1552.
|
| [17] |
Alldredge L R. Rectangular harmonic analysis applied to the geomagnetic field[J]. Journal of Geophysical Research:Solid Earth, 1981, 86(B4):3021-3026.
|
| [18] |
Cordell L. A scattered equivalent-source method for interpolation and gridding of potential-field data in three dimensions[J]. Geophysics, 1992, 57(4):629-636.
|
| [19] |
Mendonca C A, Silva J B C. The equivalent data concept applied to the interpolation of potential field data[J]. Geophysics, 1994, 59(5):722-732.
|
| [20] |
王万银, 邱之云. 一种稳定的位场数据最小曲率网格化方法研究[J]. 地球物理学进展, 2011, 26(6):2003-2010.
|
| [20] |
Wang W Y, Qiu Z Y. The research to a stable minimum curvature gridding method in potential data processing[J]. Progress in Geophysics, 2011, 26(6):2003-2010.
|
| [21] |
Li X, Götze H J. Comparison of some gridding methods[J]. The Leading Edge, 1999, 18(8):898-900.
|
| [22] |
许海红, 卢进才, 李玉宏, 等. 基于Surfer的1:50 000规则测网重力数据网格化方法选取——以银额盆地赛汉陶来区块重力资料为例[J]. 地球物理学进展, 2015, 30(6):2566-2573.
|
| [22] |
Xu H H, Lu J C, Li Y H, et al. Selection of gridding methods for 1:50,000 regular-grid gravity data based on surfer — A case from gravity data in Saihantaolai Block of Yin’e Basin[J]. Progress in Geophysics, 2015, 30(6):2566-2573.
|
| [23] |
高艳芳, 陈实, 冯斌. 交叉验证在离散数据网格化时的应用[J]. 物探化探计算技术, 2012, 34(5):619-621,504.
|
| [23] |
Gao Y F, Chen S, Feng B. Using cross validation in gridding[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2012, 34(5):619-621,504.
|
| [24] |
姚道荣, 钟波, 汪海洪, 等. 最小二乘配置与普通Kriging法的比较[J]. 大地测量与地球动力学, 2008, 28(3):77-82.
|
| [24] |
Yao D R, Zhong B, Wang H H, et al. Comparison between least square collocation and ordinary Kriging[J]. Journal of Geodesy and Geodynamics, 2008, 28(3):77-82.
|
| [25] |
刘晓刚, 吴晓平, 王凯. 扰动重力梯度张量单分量和组合分量最小二乘配置法模型的建立[J]. 地球物理学报, 2012, 55(5):1572-1580.
|
| [25] |
Liu X G, Wu X P, Wang K. Construction of the least squares collocation models for single component and composite components of disturbed gravity gradients[J]. Chinese Journal of Geophysics, 2012, 55(5):1572-1580.
|
| [26] |
Wu Y Q, Jiang Z S, Liu X X, et al. A comprehensive study of gridding methods for GPS horizontal velocity fields[J]. Pure and Applied Geophysics, 2017, 174(3):1201-1217.
|
| [27] |
Moritz H. Advanced physical geodesy[M]. Karlsruhe: Herbert Wichmann, 1980.
|
| [28] |
Goyal H K, von Frese R R B, Hinze W J, et al. Statistical prediction of satellite magnetic anomalies[J]. Geophysical Journal International, 1990, 102(1):101-111.
|
| [29] |
Langel R A, Hinze W J. The magnetic field of the earth’s lithosphere:The satellite perspective[M]. Cambridge: Cambridge University Press, 1998.
|
| [30] |
Maus S, Sazonova T, Hemant K, et al. National geophysical data center candidate for the world digital magnetic anomaly map[J]. Geochemistry,Geophysics,Geosystems, 2007, 8(6):Q06017.
|
| [31] |
Maus S, Barckhausen U, Berkenbosch H, et al. EMAG2:A 2-arc Min resolution Earth Magnetic Anomaly Grid compiled from satellite,airborne,and marine magnetic measurements[J]. Geochemistry,Geophysics,Geosystems, 2009, 10(8):Q08005.
|
| [32] |
朱晓颖, 于长春, 熊盛青, 等. 磁法在煤火探测中的应用[J]. 物探与化探, 2007, 31(2):115-119.
|
| [32] |
Zhu X Y, Yu C C, Xiong S Q, et al. The application of the magnetic method to the detection of underground coal fires[J]. Geophysical and Geochemical Exploration, 2007, 31(2):115-119.
|
| [33] |
熊盛青, 于长春. 地下煤层自燃区岩石磁性增强特征及机理研究——以内蒙古乌达和宁夏汝萁沟煤矿为例[J]. 地球物理学报, 2013, 56(8):2827-2836.
|
| [33] |
Xiong S Q, Yu C C. Characteristics and mechanisms of rock magnetic increasing in underground coal spontaneous combustion area—Take Wuda coal mine of Inner Mongolia and Ruqigou coal mine in Ningxia as examples[J]. Chinese Journal of Geophysics, 2013, 56(8):2827-2836.
|
| [34] |
Ruffhead A. An introduction to least-squares collocation[J]. Survey Review, 1987, 29(224):85-94.
|
| [35] |
郭志宏, 管志宁, 熊盛青. 长方体ΔT场及其梯度场无解析奇点理论表达式[J]. 地球物理学报, 2004, 47(6):1131-1138.
|
| [35] |
Guo Z H, Guan Z N, Xiong S Q. Cuboid ΔT and its gradient forward theoretical expressions without analytic odd points[J]. Chinese Journal of Geophysics, 2004, 47(6):1131-1138.
|
| [36] |
王家乐. 张家峁井田2-2煤烧变岩地下水流场数值模拟[D]. 西安: 西安科技大学, 2017.
|
| [36] |
Wang J L. Numerical simulation of groundwater flow field of 2-2 coal-burnt metamorphic rock in Zhangjiamao mine field[D]. Xi’'an: Xi’an University of Science and Technology, 2017.
|
| [1] |
HU Shi-Hui, MIN Gang, SUN Yi-Qin, CHEN Chun-Jiang, LI Chun-Ting, ZHANG Zhi-Hao. Gridding of complex terrains based on cluster analysis for ModEM 3D inversion[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 148-157. |
| [2] |
GONG Yi-Xuan, JIANG Kai, GAO Jing-Yu, ZHU Wan-Hua, CHEN Kai. Development of a submarine optically pumped magnetometer[J]. Geophysical and Geochemical Exploration, 2024, 48(6): 1498-1506. |
|
|
|
|

