|
|
|
| 3D forward and inverse modeling of self-potential data based on the PARDISO direct solver |
SU Zhao-Yang1( ), SHEN Jin-Song1( ), SHEN Jin-Song1( ), LUO Hui2 ), LUO Hui2 |
1.College of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China
2. Production Operation Management Department,SINOPEC Northwest Oil Field Company, Urumqi 842100, China |
|
|
|
|
Abstract In recent years, the self-potential method has played a significant role in the exploration and evaluation of seafloor massive sulfide resources. This study explored the 3D forward and inverse modeling algorithms for self-potential based on the PARDISO direct solver. First, the finite volume method was employed to discretize the self-potential control equation, and the PARDISO direct solver was utilized to improve the forward modeling efficiency. The reliability of the forward modeling algorithm was verified by comparing the numerical solution with the analytical solution. The 3D inverse modeling algorithm considered the topographic factor and incorporated the minimum support constraint and depth weighting into the objective function. The inversion results of theoretical model data effectively reconstructed the ore body structure. Finally, the self-potential data obtained from indoor sandbox experiments were inverted using the inverse modeling algorithm, obtaining that the current density anomaly was roughly consistent with the position of the metal bar. Therefore, the inverse modeling algorithm proposed in this study holds critical significance for subsequent inversion of large-scale spontaneous potential data.
|
|
Received: 10 April 2023
Published: 16 April 2024
|
|
|
|
Corresponding Authors:
SHEN Jin-Song
E-mail: 2019310419@student.cup.edu.cn;shenjinsongcup@163.com
|
|
|
|

| 模型尺寸 | 运算时间/s | 最小二乘
迭代求解器 | 共轭梯度
迭代求解器 | PARDISO
直接求解器 | | 20 × 20 × 20 | 0.15 | 0.04 | 0.005 | | 40 × 40 × 40 | 1.23 | 0.15 | 0.04 | | 60 × 60 × 60 | 5.80 | 0.89 | 0.25 |
|
Comparison between direct solver and iterative solver
|
|
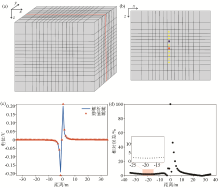
Comparison of forward response of finite volume method and analytic solutions
a—schematic diagram of mesh; b—the slice at y = 0 m (2D mesh); c—numerical and analytical solutions; d—relative error
|
|
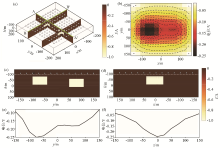
3D model and forward response results
a—model and slice position; b—plane electric field distribution collected by receiver; c—section AA' is the slice at x = 0 m; d—BB' Slices are slices located at y = -75 m; e—spontaneous potential distribution on line AA'; f—spontaneous potential distribution on line BB'
|
|
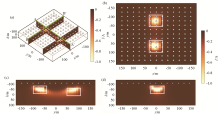
3D self-potential inversion results and slices
a—inversion result and slice position; b—slice at z=0 m; c—inversion results of profile AA'; d—inversion of profile BB' performance result
|
|
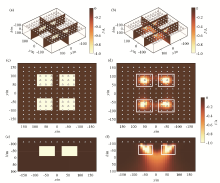
3D self-potential model and inversion results
a—inversion result and slice position; b—inversion result; c—model slice(at z=-65 m);d—inversion results of profile (slice at z = -65 m); e—model (y=-65 m); f—inversion result(y=-65 m)
|
|
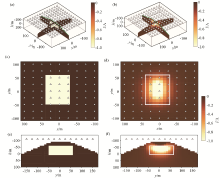
3D self-potential model and inversion results
a—3D model; b—inversion result; c—horizontal slice of model (z=-30 m);d—horizontal slice was recovered by inversion (z=-30 m); e—vertical slice of model (x=0 m); f—vertical slice was recovered by inversion (slice at x=0 m)
|

|
Observed data and predicted data obtained by inversion
a—observed data obtained by forward modeling; b—predicted data obtained from inversion; c—error between observed data and predicted data
|
|
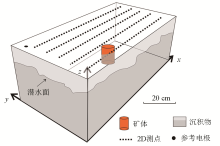
Schematic diagram of sandbox experiment
|
|
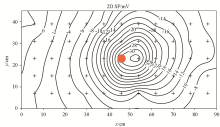
Contour diagram of self-potential distribution after the occurrence of redox reactions
|
|
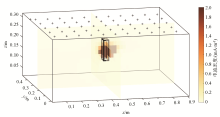
3D inversion results of sandbox experimental data
|
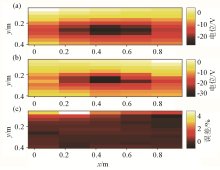
|
self-potential data from sandbox experiment and predicted data obtained by inversion
a—sandbox experiment; b—predicted data obtained from inversion; c—error between experiment data and predicted data
|
| [1] |
Jardani A, Revil A, Bolève A, et al. Three-dimensional inversion of self-potential data used to constrain the pattern of groundwater flow in geothermal fields[J]. Journal of Geophysical Research:Solid Earth, 2008, 113(B9):B09204.
|
| [2] |
Fox R W. On the electro-magnetic properties of metalliferous veins in the mines of cornwall[J]. Philosophical Transactions of the Royal Society of London, 1830, 120:399-414.

|
| [3] |
Corwin R F, Hoover D B. The self-potential method in geothermal exploration[J]. Geophysics, 1979, 44(2):226-245.

|
| [4] |
Patella D. Self-potential global tomography including topographic effects[J]. Geophysical Prospecting, 1997, 45(5):843-863.

|
| [5] |
仇勇海. 金属矿自然电位的空间分布及其应用[J]. 物探与化探, 1985, 9(4):268-273.
|
| [5] |
Qiu Y H. Spatial distribution of spontaneous potential of metallic orebody and its application[J]. Geophysical and Geochemical Exploration, 1985, 9(4):268-273.
|
| [6] |
Revil A, Ehouarne L, Thyreault E. Tomography of self-potential anomalies of electrochemical nature[J]. Geophysical Research Letters, 2001, 28(23):4363-4366.

|
| [7] |
Kawada Y, Kasaya T. Self-potential mapping using an autonomous underwater vehicle for the Sunrise deposit,Izu-Ogasawara arc,southern Japan[J]. Earth,Planets and Space, 2018, 70(1):142.
|
| [8] |
Biswas A, Sharma S P. Interpretation of self-potential anomaly over 2-D inclined thick sheet structures and analysis of uncertainty using very fast simulated annealing global optimization[J]. Acta Geodaetica et Geophysica, 2017, 52(4):439-455.

|
| [9] |
朱肖雄, 崔益安, 陈志学. 基于最小二乘正则化的自然电场场源反演成像[J]. 地球物理学进展, 2016, 31(5):2313-2318.
|
| [9] |
Zhu X X, Cui Y A, Chen Z X. Inversion for self-potential sources based on the least squares regularization[J]. Progress in Geophysics, 2016, 31(5):2313-2318.
|
| [10] |
Mendonca C A. Forward and inverse self-potential modeling in mineral exploration[J]. Geophysics, 2008, 73(1):F33-F43.
|
| [11] |
Miller C A, Kang S G, Fournier D, et al. Distribution of vapor and condensate in a hydrothermal system:Insights from self-potential inversion at mount Tongariro,new zealand[J]. Geophysical Research Letters, 2018, 45(16):8190-8198.

|
| [12] |
王文义. 海底多金属硫化物自然电位响应机理及探测方法研究[D]. 北京: 中国石油大学(北京), 2019.
|
| [12] |
Wang W Y. Study on the mechanism of self-potential and detection method of seafloor polymetallic sulfide deposits[D]. Beijing: China University of Petroleum (Beijing), 2019.
|
| [13] |
Guo Y J, Cui Y A, Xie J, et al. Seepage detection in earth-filled dam from self-potential and electrical resistivity tomography[J]. Engineering Geology, 2022, 306:106750.

|
| [14] |
Rittgers J B, Revil A, Karaoulis M, et al. Self-potential signals generated by the corrosion of buried metallic objects with application to contaminant plumes[J]. Geophysics, 2013, 78(5):EN65-EN82.
|
| [15] |
Cockett R, Heagy L J, Oldenburg D W. Pixels and their neighbors:Finite volume[J]. The Leading Edge, 2016, 35(8):703-706.

|
| [16] |
Haber E. Computational methods in geophysical electromagnetics[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2014.
|
| [17] |
Puzyrev V, Koric S, Wilkin S. Evaluation of parallel direct sparse linear solvers in electromagnetic geophysical problems[J]. Computers & Geosciences, 2016, 89:79-87.

|
| [18] |
Schenk O, Gärtner K. Two-level dynamic scheduling in PARDISO:Improved scalability on shared memory multiprocessing systems[J]. Parallel Computing, 2002, 28(2):187-197.

|
| [19] |
Bollhöfer M, Eftekhari A, Scheidegger S, et al. Large-scale sparse inverse covariance matrix estimation[J]. SIAM Journal on Scientific Computing, 2019, 41(1):A380-A401.
|
| [20] |
Barbara. Add PARDISO lib to Matlab in Windows 10, 2023,https://www.mathworks.com/matlabcentral/fileexchange/119053-add-pardiso-lib-to-matlab-in-windows-10

|
| [21] |
Revil A, Jardani A. The self-potential method:Theory and applications in environmental geosciences[M]. Cambridge: Cambridge University Press, 2013.
|
| [22] |
Portniaguine O, Zhdanov M S. 3D magnetic inversion with data compression and image focusing[J]. Geophysics, 2002, 67(5):1532.

|
| [23] |
Nocedal J, Wright S J, Numerical optimization[M]. New York: Springer New York,1999.
|
| [24] |
Golub G H, von Matt U.Generalized cross-validation for large-scale problems[J]. Journal of Computational and Graphical Statistics, 1997, 6(1):1.
|
| [25] |
Mao D Q, Revil A. Induced polarization response of porous media with metallic particles—Part 3:A new approach to time-domain induced polarization tomography[J]. Geophysics, 2016, 81(4):D345-D357.
|
| [26] |
Zhdanov M S. Geophysical inverse theory and regularization problems[M]. Amsterdam:Elserier, 2002.
|
| [27] |
Li Y G, Oldenburg D W. 3D inversion of magnetic data[J]. Geophysics, 1996, 61(2):394-408.

|
| [28] |
侯振隆. 重力全张量梯度数据的并行反演算法研究及应用[D]. 长春: 吉林大学, 2016.
|
| [28] |
Hou Z L. Research and application of the parallel inversion algorithms based on the full tensor gravity gradiometry data[D]. Changchun: Jilin University, 2016.
|
| [29] |
Zhdanov M, Tolstaya E. Minimum support nonlinear parametrization in the solution of a 3D magnetotelluric inverse problem[J]. Inverse Problems, 2004, 20(3):937-952.

|
| [30] |
汪轩. 基于先验信息约束的电磁和地震结构耦合联合反演研究[D]. 北京: 中国石油大学(北京), 2020.
|
| [30] |
Wang X. Structural-coupled Joint Inversion of Electromagnetic and Seismic Data Based on a priori Information Constraint[D]. Beijing: China University of Petroleum (Beijing), 2020.
|
|
|
|

