|
|
|
| A regularization theory-based method for time-frequency analysis and its applications |
ZHANG Jin-Qiang1,2,3( ) ) |
1. Key Laboratory of Shale Oil and Gas Exploration & Production,Sinopec,Beijing 102206,China
2. Sinopec Petroleum Exploration and Production Research Institute,Beijing 102206,China
3. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development,Beijing 100026,China |
|
|
|
|
Abstract Time-frequency analysis (TFA) has been widely used in seismic exploration,thus it is crucial to develop a TFA algorithm with high time-frequency resolution.Given the limitations of conventional TFA methods,this study proposed a TFA method based on the regularization theory.The proposed method considers the signal in a short-time window as a superposition of harmonics with different frequencies and takes the TFA problem as an inverse problem.From this perspective,the TFA problem is ill-posed and needs to be solved based on the regularization theory to get a significant time-frequency spectrum.The solution methods under the conditions of L1 and L2 norm constraints and the minimum support constraint are commonly used in the regularization theory.This study investigated these solution methods and unified them into the same solution framework.Numerical analysis shows that the TFA method under the condition of the minimum support constraint yielded high time-frequency resolution.This method was systematically applied to the actual data of a specific study area,producing a time-frequency data volume with high time-frequency resolution.Moreover,the planar reservoir distribution was clearly characterized using a single-frequency data volume,demonstrating the promising application prospect of the method.
|
|
Received: 22 July 2022
Published: 11 October 2023
|
|
|
|
|
|
fig.1a and fig.1b
">
|
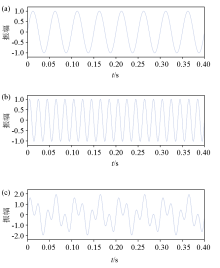
Synthetic signal of the two sinuasoidal signals
a—sinuasoidal signal of 20 Hz;b—sinuasoidal signal of 50 Hz;c—summary signal of fig.1a and fig.1b
|
|
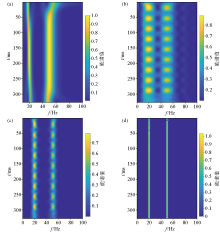
Comparisons of time-frequency spectrum of different time frequency analysis method
a—time-frequency spectrum of CWT;b—time-frequency spectrum of RL2TFS;c—time-frequency spectrum of RL1TFS;d—time-frequency spectrum of RMSTFS
|
fig. 3b) obtained by different time-frequency method
">
|
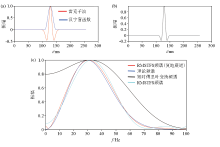
40 ms Hanning function applied on the ricker wavelet and the correpsonding spectrum
a—40 ms Hanning function and Riker wavelet;b—signal obtained by applying Hanning on ricker wavelet;c—frequency spectrum of the signal (fig. 3b) obtained by different time-frequency method
|
fig. 4b) obtained by different time-frequency method
">
|
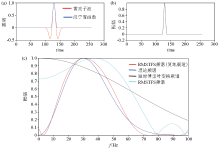
20 ms Hanning function applied on the ricker wavelet and the correpsonding spectrum
a—20 ms Hanning function and Riker Wavelet;b—signal obtained by applying Hanning on ricker wavelet;c—frequency spectrum of the signal(fig. 4b) obtained by different time-frequency method
|

|
Synthetic record of different thikness layers with same recflction coefficient on top and bottom and the corresponding time-frequency spectrum
a—seismic reflection series;b—synthetic record;c—spectrum of CWT;d—spectrum of RMSTFS
|

|
Synthetic record of different thikness layers with revese recflction coefficients on top and bottom and the corresponding time-frequency spectrum
a—seismic reflection series;b—synthetic record;c—spectrum of CWT;d—spectrum of RMSTFS
|
fig. 5a;b—the frequency response curves for reflection paris of fig. 6a
">
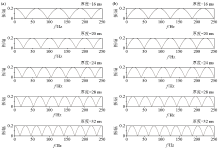
|
The frequency response curves of reflection pairs with different time thickness
a—the frequency response curves for reflection paris of fig. 5a;b—the frequency response curves for reflection paris of fig. 6a
|
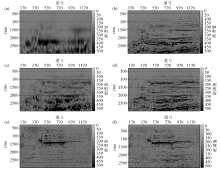
|
Sections of different frequency spectrum obtained by CWT and RMSTFS
a—section of 10 Hz spectral spectrum of CWT;b—section of 10 Hz spectral spectrum of RMSTFS;c—section of 20 Hz spectral spectrum of CWT;d—section of 20 Hz spectral spectrum of RMSTFS;e—section of 60 Hz spectral spectrum of CWT;f—section of 60 Hz spectral spectrum of RMSTFS
|
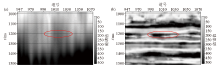
|
Comparisons of 10 Hz spectrum section obtained by CWT and RMSTFS
a—section of 10 Hz spectral spectrum of CWT(zoomed);b—section of 10 Hz spectral spectrum of RMSTFS(zoomed)
|
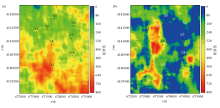
|
Horizon slices of 10 Hz spectrum by different algorithms
a—Horizon slice of 10 Hz CWT spectrum;b—Horizon slice of 10 Hz RMSTFS spectrum
|
| [1] |
曹思远, 袁殿. 高分辨率地震资料处理技术综述[J]. 新疆石油地质, 2016, 37(1):112-119.
|
| [1] |
Cao S Y, Yuan D. A review of high-resolution seismic data processing approaches[J]. Xinjiang Petroleum Geology, 2016, 37(1):112-119.
|
| [2] |
张恒磊, 张云翠, 宋双, 等. 基于Curvelet域的叠前地震资料去噪方法[J]. 石油地球物理勘探, 2008, 43(5):508-513.
|
| [2] |
Zhang H L, Zhang Y C, Song S, et al. Curvelet domain-based prestack seismic data denoise method[J]. Oil Geophysical Prospecting, 2008, 43(5):508-513.
|
| [3] |
王云专, 金兰涛, 龙玉沙. 基于S变换的随机噪声压制方法[J]. 地球物理学进展, 2010, 25(2):562-567.
|
| [3] |
Wang Y Z, Jin L T, Long Y S. The method for attenuating random noise based on S transform[J]. Progress in Geophysics, 2010, 25(2):562-567.
|
| [4] |
胡瑞卿, 何俊杰, 李华飞, 等. 时频域变分模态分解地震资料去噪方法[J]. 石油地球物理勘探, 2021, 56(2):257-264.
|
| [4] |
Hu R Q, He J J, Li H F, et al. Seismic data de-noising method on VMD in time-frequency domain[J]. Oil Geophysical Prospecting, 2021, 56(2):257-264.
|
| [5] |
曲中党, 贺日政, 张训华, 等. 时频域相位滤波在远震接收函数噪声压制中的应用[J]. 地球物理学报, 2017, 60(4):1389-1397.
|
| [5] |
Qu Z D, He R Z, Zhang X H, et al. The time frequency domain phase filter and its application in noise suppression of teleseismic receiver functions[J]. Chinese Journal of Geophysics, 2017, 60(4):1389-1397.
|
| [6] |
朱振宇, 高佳伦, 姜秀娣, 等. 基于三参数小波的频谱分解方法[J]. 石油地球物理勘探, 2018, 53(6):1299-1306.
|
| [6] |
Zhu Z Y, Gao J L, Jiang X D, et al. Spectrum decomposition based on three-parameter wavelet[J]. Oil Geophysical Prospecting, 2018, 53(6):1299-1306.
|
| [7] |
曹军, 王林飞, 葛学胜, 等. 分频道积分技术在苏59气田储层预测中的应用[J]. 工程地球物理学报, 2020, 17(2):154-159.
|
| [7] |
Cao J, Wang L F, Ge X S, et al. Application of frequency-shared trace integration technique to reservoir prediction in Su59 gas field[J]. Chinese Journal of Engineering Geophysics, 2020, 17(2):154-159.
|
| [8] |
乐友喜, 蔡俊雄, 李斌, 等. 同步挤压小波变换在储层预测中的应用研究[J]. 地球物理学进展, 2018, 33(6):2498-2506.
|
| [8] |
Yue Y X, Cai J X, Li B, et al. Application research of synchrosqueezing wavelet transform in the reservoir prediction[J]. Progress in Geophysics, 2018, 33(6):2498-2506.
|
| [9] |
杨亚迪, 曾庆才, 郭晓龙, 等. 基于匹配追踪算法的高精度页岩气“甜点”识别[J]. 科学技术与工程, 2017, 17(4):180-185.
|
| [9] |
Yang Y D, Zeng Q C, Guo X L, et al. High-precision seismic prediction of shale gas sweet spots based on matching pursuit algorithm[J]. Science Technology and Engineering, 2017, 17(4):180-185.
|
| [10] |
李振春, 刁瑞, 韩文功, 等. 线性时频分析方法综述[J]. 勘探地球物理进展, 2010, 33(4):239-246.
|
| [10] |
Li Z C, Diao R, Han W G, et al. Review on linear time frequency analysis methods[J]. Progress in Exploration Geophysics, 2010, 33(4):239-246.
|
| [11] |
李传辉, 张繁昌, 印兴耀. 三种线性时频分析方法的影响因素及精度分析[J]. 石油天然气学报:江汉石油学院学报, 2010, 32(4):239-242.
|
| [11] |
Li C H, Zhang F C, Yin X Y. The influential factors and accuracy of three time-freqency analyses[J]. Journal of Oil and Gas Technology:J. JPI, 2010, 32(4):239-242.
|
| [12] |
Qian S, Chen D. Discrete Gabor transform[J]. IEEE Transactions on Signal Processing, 1993, 41(7):2429-2439.

|
| [13] |
Sinha S, Routh P, Anno P. Instantaneous spectral attributes using scales in continuous-wavelet transform[J]. Geophysics, 2009, 74(2):WA137-WA142.

|
| [14] |
李思源, 徐天吉. 基于Wigner-Ville分布于Chrip-Z变换的高分辨率时频分析方法[J]. 石油地球物理勘探, 2022, 57(1):168-175.
|
| [14] |
Li S Y, Xu T J. A new high-resolution time-freqency method based on Wigner-Ville distribution and Chrip-Z transform[J]. Oil Geophysical Prospecting, 2022, 57(1):168-175.
|
| [15] |
张晓燕, 彭真明, 张萍, 等. 基于分数阶Wigner-Ville分布的地震信号谱分解[J]. 石油地球物理勘探, 2014, 49(5):839-845.
|
| [15] |
Zhang X Y, Peng Z M, Zhang P, et al. Spectral decomposition of seismic signals based on fractional Wigner-Ville distribution[J]. Oil Geophysical Prospecting, 2014, 49(5):839-845.
|
| [16] |
Han J, Van D B M. Empirical mode decomposetion for seismic time-freqency analysis[J]. Geophysics, 2013, 78(2):O9-O19.

|
| [17] |
Wang Y H. Seismic time-frequency spectral decom-position by matching pursuit[J]. Geophysics, 2007, 72(1):V13-V20.

|
| [18] |
Mallat S, Zhang Z. Matching pursuit with time-freqency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(2):3397-3415.

|
| [19] |
Puryear C I, Portniaguine O N, Cobos C M, et al. Constraint least-square spectral analysis:Application to seismic data[J]. Geophysics, 2012, 77(5):V143-V167.

|
| [20] |
李海英, 武国宁, 陈小民. 最小二乘约束下的频谱分析技术及其应用[J]. 地球物理学进展, 2014, 29(6):2685-2689.
|
| [20] |
Li H Y, Wu G N, Chen X M. Least square constraint time frequency method and its application[J]. Progress in Geophysics, 2014, 29(6):2685-2689.
|
| [21] |
田琳, 胡津. 稀疏短时傅里叶变换谱分解方法及应用[J]. 地球物理学进展, 2021, 36(6):2581-2587.
|
| [21] |
Tian L, Hu J. Sparse shot-time Fourier transform spectral decomposition method and its application[J]. Progress in Geophysics, 2021, 36(6):2581-2587.
|
| [22] |
Zhang R, John C. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6):R147-R158.

|
| [23] |
Portniaguine O, Zhdanov M S. Focusing geophysical inversion images[J]. Geophysics, 1999, 64(3):874-887.

|
| [24] |
Portniaguine O, Zhdanov M S. 3D magnetic inversion with data compression and image focusing[J]. Geophysics, 2002, 67(5):1532-1541.

|
| [25] |
Partyka G A, Gridley J A, Lopez J A. Interpretational aspects of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(2):353-360.

|
| [1] |
HUANG Wei, ZHOU Jie, GAO Li-Jun, WANG Sheng-Li, YAN Hai-Tao. The application of frequency division ant tracking based on synchronous extrusion improvement of short time Fourier transform in crack detection[J]. Geophysical and Geochemical Exploration, 2021, 45(2): 432-439. |
| [2] |
HE Wen, CAI Jia-Ming, SONG Zhi-Hua, LI Hai-Yin, ZHANG Hao, HUANG Kong-Zhi, GUAN Yan-Bin. Sedimentary cycle division using peak frequency of time-frequency Teager-Kaiser energy[J]. Geophysical and Geochemical Exploration, 2020, 44(6): 1336-1344. |
|
|
|
|

