|
|
|
| Globally optimized seismic impedance inversion with lateral constraints and its application |
ZHU Jian-Bing1( ), GAO Zhao-Qi2, TIAN Ya-Jun2, LIANG Xing-Cheng2 ), GAO Zhao-Qi2, TIAN Ya-Jun2, LIANG Xing-Cheng2 |
1. Geophysical Research Institute,Shengli Oilfield Branch Company of Sinopec,Dongying 257022,China
2. School of Information and Communications Engineering,Xi'an Jiaotong University,Xi'an 710049,China |
|
|
|
|
Abstract The seismic impedance inversion is nonlinear optimization based on seismic data to obtain wave impedance parameters.The global optimization algorithm independent of the gradient information of objective function is an effective method for seismic impedance inversion.However,this method adopts a trace-by-trace inversion strategy and ignores the spatial correlation of adjacent seismic traces,resulting in poor lateral continuity of the inversion results.Given this,this study proposed a model space initialization method integrating the optimal solution of the bypass to restrict the search space of wave impedance inversion,in order to improve the lateral continuity of inversion results.Based on this,this study proposed a seismic impedance inversion method with lateral constraints based on multi-group variation differential evolution.A case of synthetic seismogram shows that this method has a higher convergence rate and better lateral continuity of inversion results than conventional methods.This method was applied to the inversion of reservoir impedance parameters of a block of the Shengli Oilfield.The obtained inversion results were in good agreement with the logging data and effectively characterize the thickness of reservoir sandstone.
|
|
Received: 01 November 2021
Published: 03 January 2023
|
|
|
|
|
|
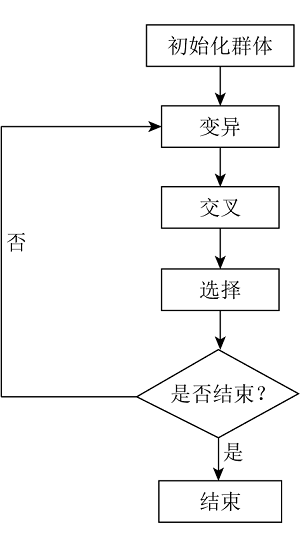
|
Flowchart of MMDE
|

|
Comparison of the search space of different methods
a—the search space of MMDE;b—the search space of the proposed method with lateral constraints
|
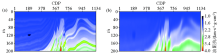
|
Marmousi II impedance model
a—true impedance model;b—the initial impedance model used in inversion
|
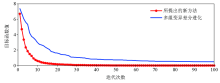
|
Convergence curves of the proposed method and conventional MMDE
|
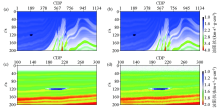
|
Comparison of inverted impedance model of different methods
a—impedance model inverted by the proposed method inversion;b—impedance model inverted by MMDE;c、d—are the enlarged portions of a and b at CDP100~300
|

| 参数 | 多组变异差分进化算法 | 所提出新方法 | | 信噪比SNR/dB | 33.2153 | 36.0658 | | 结构相似性指数SSIM | 0.8682 | 0.9332 |
|
Quantitative comparison of the quality of impedance models obtained by different inversion methods
|
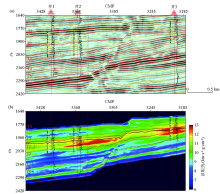
|
Comparison of cross-well sections
a—seismic profile;b—impedance;the black curve at the well point is the impedance calculated from well-log data
|
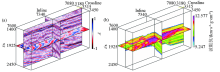
|
Field data example
a—3D poststack seismic data from Shengli oilfield;b—inverted impedance model of the proposed method
|
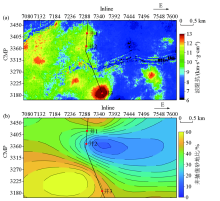
|
Comparison between inverted impedance model and well-log interpretation results
a—impedance model along horizon T2_1;b—well interpolation sand ground ratio profile
|
| [1] |
万晓明, 梁劲, 梁金强, 等. 叠后波阻抗无井反演技术在T研究区天然气水合物分布预测中的应用[J]. 物探与化探, 2016, 40(3):438-444.

|
| [1] |
Wan X M, Liang J, Liang J Q, et al. The application of post-stack impedance inversion without well to the prediction of gas hydrate distribution in T study area[J]. Geophysical and Geochemical Exploration, 2016, 40(3):438-444.

|
| [2] |
孔省吾, 张云银, 沈正春, 等. 波形指示反演在灰质发育区薄互层浊积岩预测中的应用——以牛庄洼陷沙三中亚段为例[J]. 物探与化探, 2020, 44(3):665-671.

|
| [2] |
Kong X W, Zhang Y Y, Shen Z C, et al. The application of waveform inversion prediction of thin turbidite reservoir to calcareous depositional area: A case study of $E_{3}s^{2}_{3}$ in Niuzhuang sag[J]. Geophysical and Geochemical Exploration, 2020, 44(3): 665-671.

|
| [3] |
汪玲玲, 高静怀, 赵谦, 等. 基于矩阵Toeplitz稀疏分解的相对波阻抗反演方法[J]. 地球物理学报, 2017, 60(2):639-654.
|
| [3] |
Wang L L, Gao J H, Zhao Q, et al. Relative acoustic impedance inversion via Toeplitz-Sparse Matrix Factorization[J]. Chinese Journal of Geophysics, 2017, 60(2):639-654.
|
| [4] |
Frank M S, Balanis C A. A conjugate direction method for geophysical inversion problems[J]. IEEE Transactions on Geoscience and Remote Sensing, 1987,(6):691-701.
|
| [5] |
Deift P, Zhou X. A steepest descent method for oscillatory Riemann-Hilbert problems[J]. Appeared in Bulletin of the American Mathematical Society, 1992, 26(1):119-124.
|
| [6] |
Ma X Q. Simultaneous inversion of prestack seismic data for rock properties using simulated annealing[J]. Geophysics, 2002, 67(6):1877-1885.

|
| [7] |
Lagos S R, Sabbione J I, Velis D R. Very fast simulated annealing and particle swarm optimization for microseismic event location[C]// SEG Technical Program Expanded Abstracts 2014, 2014.
|
| [8] |
Donelli M, Franceschini G, Martini A, et al. An integrated multiscaling strategy based on a particle swarm algorithm for inverse scattering problems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(2):298-312.

|
| [9] |
Fernandez Martinez J L, Mukerji T, Garcia Gonzalo E, et al. Reservoir characterization and inversion uncertainty via a family of particle swarm optimizers[J]. Geophysics, 2012, 77(1):M1-M16.

|
| [10] |
Parolai S, Picozzi M, Richwalski S M, et al. Joint inversion of phase velocity dispersion and H/V ratio curves from seismic noise recordings using a genetic algorithm,considering higher modes[J]. Geophysical Research Letters, 2005, 32(1).
|
| [11] |
Govindan R, Kumar R, Basu S, et al. Altimeter-derived ocean wave period using genetic algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 8(2):354-358.

|
| [12] |
Li T, Mallick S. Multicomponent,multi-azimuth pre-stack seismic waveform inversion for azimuthally anisotropic media using a parallel and computationally efficient non-dominated sorting genetic algorithm[J]. Geophysical Journal International, 2015, 200(2):1136-1154.

|
| [13] |
Semnani A, Kamyab M, Rekanos I T. Reconstruction of one-dimensional dielectric scatterers using differential evolution and particle swarm optimization[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4):671-675.

|
| [14] |
Dehmollaian M. Through-wall shape reconstruction and wall parameters estimation using differential evolution[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 8(2):201-205.

|
| [15] |
Pan Z, Wu J, Gao Z, et al. Adaptive differential evolution by adjusting subcomponent crossover rate for high-dimensional waveform inversion[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(6):1327-1331.

|
| [16] |
Li Z, Hao T, Xu Y, et al. A global optimizing approach for waveform inversion of receiver functions[J]. Computers & Geosciences, 2010, 36(7): 871-880.

|
| [17] |
Potter M A, Jong K. A cooperative coevolutionary approach to function optimization[C]// Springer: Parallel Problem Solving from Nature,Heidelberg, 1994.
|
| [18] |
Wang C, Gao J. High-dimensional waveform inversion with cooperative coevolutionary differential evolution algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 9(2):297-301.

|
| [19] |
Gao Z, Pan Z, Gao J. Multimutation differential evolution algorithm and its application to seismic inversion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(6):3626-3636.

|
| [20] |
Gholami A. Nonlinear multichannel impedance inversion by total-variation regularization[J]. Geophysics, 2015, 80(5):R217-R224.

|
| [21] |
Zhang S, Fan X, Li G, et al. Multi-trace blocky reflectivity inversion with anisotropic total variation regularization[C]// SEG Technical Program Expanded Abstracts 2019, 2019.
|
| [22] |
Cheng L, Wang S, Li S, et al. Multi-trace nonstationary sparse inversion with structural constraints[J]. Acta Geophysica, 2020, 68(3):675-685.

|
| [1] |
YUE Hang-Yu, WANG Xiao-Jiang, WANG Lei, CHEN Xiao-Qiang, JIANG Chun-Xiang, LI Pei, ZHANG Bao-Wei. Key techniques for seismic data processing of deep metal deposits:A case study of the Chaganhua molybdenum orefield in Inner Mongolia[J]. Geophysical and Geochemical Exploration, 2022, 46(6): 1315-1326. |
| [2] |
Rui-Qing HU, Yan-Chun WANG, Zhan-Wei YUE, Qi WANG. Feature extraction in wavelet domain and its application to shallow seismic data surface-wave suppression[J]. Geophysical and Geochemical Exploration, 2018, 42(6): 1228-1236. |
|
|
|
|

