|
|
|
| Inversion of magnetic resonance sounding under the condition of surface slope |
LI Fan1( ), ZHOU Ming2, LI Kai-Tian1, LU Kai1, LI Zhen-Yu1( ), ZHOU Ming2, LI Kai-Tian1, LU Kai1, LI Zhen-Yu1( ) ) |
1. Institute of Geophysics & Geomatics, China University of Geosciences(Wuhan), Wuhan 430074,China
2. Guangxi Communications Design Group Co.,Ltd., Nanning 530012,China |
|
|
|
|
Abstract Magnetic resonance sounding is a geophysical exploration method based on the difference of relaxation characteristics of hydrogen proton in geomagnetic field. It can detect the content and distribution of groundwater without damage. In recent years, with the expansion of the application of magnetic resonance sounding, this method is often faced with the detection when the surface has a large slope. When traditional inversion methods are used, inaccurate inversion results often occur. In this paper, the angle between the geomagnetic field vector and the coil is introduced, which is called the effective geomagnetic inclination, and the inversion method of the magnetic resonance sounding under surface slope is given. According to the prior information provided by geological data or other geophysical methods, the distribution of parallel or horizontal layered kernel functions of the magnetic resonance sounding is obtained, so as to carry out the inversion of the NMR signal under the condition of surface slope. In this paper, 1D and 2D aquifer models are constructed with the sloping surface, the corresponding NMR signals are obtained by forward calculation, and the kernel functions calculated by effective geomagnetic inclination and traditional method are used for inversion. The results show that, in the case of surface slope, the traditional inversion method of magnetic resonance sounding will inevitably produce errors, while the kernel function calculated by effective geomagnetic inclination can suppress the influence of surface slope. The validity and feasibility of the method were verified by the inversion of the filed NMR data in Baishuihe landslide area. Therefore, the inversion method based on the effective geomagnetic inclination proposed in this paper can greatly improve the application scope of magnetic resonance sounding.
|
|
Received: 07 May 2020
Published: 27 July 2021
|
|
|
|
Corresponding Authors:
LI Zhen-Yu
E-mail: lifan@cug.edu.cn;zhenyuli626@126.com
|
|
|
|
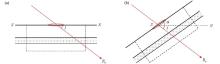
|
Schematic diagram of the angle relationship between the coil and the geomagnetic field
a—horizon;b—inclined surface
|
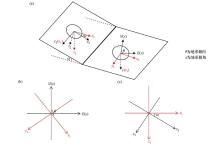
|
Diagram of the coordinate transformation under the condition of horizontal and inclined surface
a—the schematic diagram of angle relationship of horizontal coordinate(x,y,z), auxiliary coordinate(x1,y1,z1) and tilt coordinate (x2,y2,z2);b—the schematic diagram of angle relationship between horizontal coordinate and auxiliary coordinate;c—the schematic diagram of angle relationship between auxiliary coordinate and tilt coordinate
|

|
Cross section of the MRS kernel function under different terrain inclination
a—α=0°;b—α=30°;c—α=45°;d—α=90°;each subplot has been placed according to the real dip angle, and the red coordinate axis is the horizontal coordinate system. The parameters used in calculation are:Tx/Rx is a circle with the radius of 10 m, 2 turns. The underground resistivity is 100 Ω·m, the excitation pulse moment is 10 A·s, the geomagnetic inclination is 45°N, the dip direction is south, and the geomagnetic declination is 0°
|
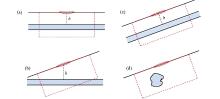
|
Diagram of underground aquifers distribution
a—horizontal aquifers in horizontal terrain; b—horizontal aquifer layers in inclined terrain; c—parallel aquifer layers in inclined terrain; d—2D aquifers distributed along the trend in inclined terrain
|
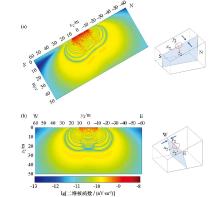
|
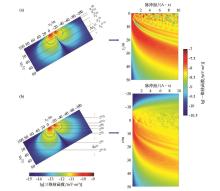
Schematic diagram of 2D kernel function calculation in case of inclined surface
a—the 2D kernel function distributed along the dip direction; b—the 2D kernel function distributed along the trend direction. The attached subplot on the right is the schematic diagram of spatial geometric position;the calculation parameters are:Tx/Rx is a circle with radius of 10 m, 2 turns. The underground resistivity is 100 Ω·m, the terrain dip angle is 30°, the dip direction is south, the geomagnetic inclination is 45°N, and the geomagnetic declination is 0°. The excitation pulse moment is 10 A·s
|
|
Schematic diagram of 1D kernel function calculation in case of inclined surface
a—parallel stratification; b—horizontal stratification
|
|
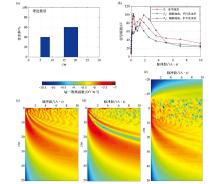
Diagram of 1D aquifer setting and kernel function distribution in condition of surface slope
a—theoretical aquifer model, which represents that the aquifer is located at 5~9 m and 15~21 m underground; b—the relationship between the initial amplitude of NMR signal and the excitation pulse moment of the parallel aquifer, the horizontal aquifer and the aquifer with no topographic inclination; c—kernel function distribution in horizontal terrain; d—kernel function distribution of parallel stratification in inclined terrain; e—kernel function distribution of horizontal stratification in inclined terrain
|
|
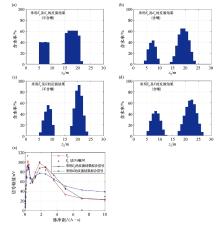
1D inversion result of NMR signal in case of parallel stratification
a~d—the inversion results ofEp using parallel kernel function Kp after topographic correction and the uncorrected kernel function K, respectively; e—the fitting results of inversion data
|
|
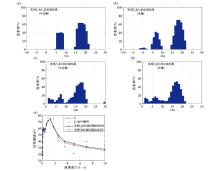
1D inversion result of NMR signal in case of horizontal stratification
a~d—the inversion results ofEh using horizontal kernel function Kh after topographic correction and the uncorrected kernel function K, respectively; e—the fitting results of inversion data
|

|
Diagram of 2D aquifer setting and forward modeling result of NMR signal in case of inclined surface
a—the theoretical aquifer model, the red triangle in the figure represents the position of the center point of theTx/Rx coil; b—the theoretical NMR signal for each coil
|
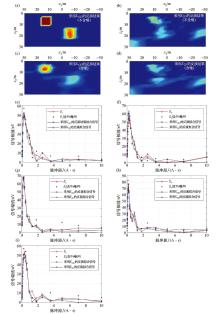
|
2D inversion result of NMR signal in case of inclined surface
a~d—represents the inversion results using the kernel functionKs2D after topographic correction and K2D without topographic correction with or without 5% Gaussian white noise, respectively;e~i—the fitting results of inversion data for each coil
|

|
Geological section of Baishuihe landslide
a—photo of the study area;b—geological section of Baishuihe lanslide
|

|
Comparison of inversion results of Baishuihe landslide by MRS method
a—inversion results of measuring point 01; b—inversion results of measuring point 02;the red dotted line in the figure indicates the position of the landslide mass calibrated by the borehole
|
| [1] |
潘玉玲, 张昌达. 地面核磁共振找水理论和方法 [M]. 武汉: 中国地质大学出版社, 2000.
|
| [1] |
Pan Y L, Zhang C D. Theory and method of surface nuclear magnetic resonance [M]. Wuhan: China University of Geosciences Press, 2000.
|
| [2] |
潘玉玲, 万乐, 袁照令, 等. 核磁共振找水方法的现状和发展趋势[J]. 地质科技情报, 2000, 19(1):105-108.
|
| [2] |
Pan Y L, Wan L, Yuan Z L, et al. Current status and development theory of detecting underground water with nuclear magnetic resonance[J]. Geological Science and Technology Information, 2000, 19(1):105-108.
|
| [3] |
马国凯, 李振宇. 综合物探技术在滑坡监测中的应用研究[J]. 工程地球物理学报, 2016, 13(2):191-195.
|
| [3] |
Ma G K, Li Z Y. The Application of comprehensive geophysical prospecting technology to landslide monitoring[J]. Chinese Journal of Engineering and Geophysics, 2016, 13(2):191-195.
|
| [4] |
Irons T, Quinn M C, Li Y, et al. A numerical assessment of the use of surface nuclear magnetic resonance to monitor internal erosion and piping in earthen embankments[J]. Near Surface Geophysics, 2014, 12(2):325-334.

|
| [5] |
蒋川东, 林君, 秦胜武, 等. 磁共振方法在堤坝渗漏探测中的实验[J]. 吉林大学学报:工学版, 2012, 42(3):858-863.
|
| [5] |
Jiang C D, Lin J, Qin S W, et al. Experiment on dam leakage detection with magnetic resonance sounding[J]. Journal of Jilin University:Earth Science Edition, 2012, 42(3):858-863.
|
| [6] |
鲁恺, 朱源婷, 马国凯, 等. 地面核磁共振方法在石质文物保护中的应用[J]. 文物保护与考古科学, 2018, 30(6):92-97.
|
| [6] |
Lu K, Zhu Y T, Ma G K, et al. Application of surface nuclear magnetic resonance (SNMR) to protection of stone relics[J]. Sciences of Conservation and Archaeology, 2018, 30(6):92-97.
|
| [7] |
潘剑伟, 占嘉诚, 洪涛, 等. 地面核磁共振方法和高密度电阻率法联合找水[J]. 地质科技情报, 2018, 37(3):253-262.
|
| [7] |
Pan J W, Zhan J C, Hong T, et al. Using the combination of SNMR method and multi-electrode resistivity method in detecting groundwater[J]. Geological Science and Technology Information, 2018, 37(3):253-262.
|
| [8] |
Girard J F, Legchenko A, Boucher M, et al. Numerical study of the variations of magnetic resonance signals caused by surface slope[J]. Journal of Applied Geophysics, 2008, 66(3):94-103.

|
| [9] |
Rommel I H M, Yaramanci U. The effect of topography on MRS measurements with separated loops[M]. 3rd Magnetic Resonance Sounding International Workshop: A reality in applied Hydrogeophysics: MRS2006 Proceedings. 2006.
|
| [10] |
Lehmann-Horn J A, Hertrich M, Greenhalgh S A, et al. Three-dimensional magnetic field and NMR sensitivity computations incorporating conductivity anomalies and variable-surface topography[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(10):3878-3891.
|
| [11] |
Greben J M, Meyer R, Kimmie Z. The underground application of magnetic resonance soundings[J]. Journal of Applied Geophysics, 2011, 75(2):220-226.

|
| [12] |
任志平, 李貅, 戚志鹏, 等. 地面核磁共振三维响应影响因素[J]. 物探与化探, 2017, 41(1):92-97.
|
| [12] |
Ren Z P, Li X, Qi Z P, et al. An analysis of factors affecting SNMR 3D response[J]. Geophysical and Geochemical Exploration, 2017, 41(1):92-97.
|
| [13] |
李振宇, 唐辉明, 潘玉玲. 地面核磁共振方法在地质工程中的应用 [M]. 武汉: 中国地质大学出版社, 2006.
|
| [13] |
Li Z Y, Tang H M, Pan Y L. The application of surface nuclear magnetic resonance method in Geological Engineering [M]. Wuhan: China University of Geosciences Press, 2006.
|
| [14] |
Mcelhinny M, Mcfadden P L. The magnetic field of the earth: paleomagnetism, the core, and the deep mantle [M]. New York: Academic Press, 1998.
|
| [15] |
Legchenko A, Valla P. A review of the basic principles for proton magnetic resonance sounding measurements[J]. Journal of Applied Geophysics, 2002, 50(1-2):3-19.

|
| [16] |
Weichman P B, Lavely E M, Ritzwoller M H. Theory of surface nuclear magnetic resonance with applications to geophysical imaging problems[J]. Physical Review E, 2000, 62(1):1290-1312.

|
| [17] |
余永鹏, 李振宇, 龚胜平, 等. 1D SNMR吉洪诺夫正则化反演方法研究[J]. CT理论与应用研究, 2009, 18(2):1-8.
|
| [17] |
Yu Y P, Li Z Y, Gong S P, et al. The research on 1D SNMR inversion by Tikhonov regularization method[J]. CT Theory and Applications, 2009, 18(2):1-8.
|
| [18] |
Mueller-Petke M, Costabel S. Comparison and optimal parameter settings of reference-based harmonic noise cancellation in time and frequency domains for surface-NMR[J]. Near Surface Geophysics, 2014, 12(2):199-210.

|
| [1] |
LIU Bao, YANG Yu-Shan, LIU Tian-You. Metallogenic prospect prediction and 3D geological modeling for the Tonglyushan ore field[J]. Geophysical and Geochemical Exploration, 2023, 47(4): 906-915. |
| [2] |
ZHANG Yang-Yang, DU Wei, WANG Zhi-Shui, MIAO Xu-Huang, ZHANG Xiang. Application of particle swarm algorithm based on Lévy flight in magnetotelluric inversion[J]. Geophysical and Geochemical Exploration, 2023, 47(4): 986-993. |
|
|
|
|

