|
|
|
| A low-rank decomposition-based method for separating gravity and magnetic anomalies and its application |
ZHANG Zi-Wei1,2,3( ), LI Hou-Pu4( ), LI Hou-Pu4( ), ZHANG Heng-Lei1,2, ZHU Dan5 ), ZHANG Heng-Lei1,2, ZHU Dan5 |
1. School of Geophysics and Geomatics, China University of Geosciences(Wuhan), Wuhan 430074, China
2. Key Laboratory of Geological Survey and Evaluation of Ministry of Education, China University of Geosciences (Wuhan), Wuhan 430074, China
3. No. 2 Gas Production Plant, North China Oil and Gas Branch, SINOPEC, Xianyang 712000, China
4. School of Electrical Engineering, Naval University of Engineering, Wuhan 430033, China
5. School of Geosciences, China University of Petroleum (East China), Qingdao 266580, China |
|
|
|
|
Abstract Effectively separating target anomalies while minimizing over- or under-separation remains challenging in gravity and magnetic field separation. In this study, the low-rank decomposition was employed to separate gravity and magnetic anomalies. Additionally, to determine the balance parameters that affect potential field separation, this study proposed an optimal estimation method based on the minimum correlation coefficient. Tests of various separation methods based on theoretical gravity and magnetic anomaly models demonstrate that the proposed method allows for effective separation, significantly reducing under- or over-separation caused by the sliding window average and wavelet analysis methods. The proposed method was applied to the Bouguer gravity anomaly data from a mining area in western China. The separated local anomalies clearly reflected the presence of rock and/or ore bodies with low magnetic susceptibility and high density. Model experiments and field applications demonstrate that the proposed method can enhance the accuracy and practicality of potential field separation.
|
|
Received: 07 April 2024
Published: 26 February 2025
|
|
|
|
|
|

| 模型 | 中心坐标/m | 中心深度/
m | 尺寸/m | 磁化强度/
(A·m-1) | | A:球体 | (300,750) | 50 | r=50 | 2 | | B:球体 | (1 200,750) | 300 | r=100 | 10 | | C:棱柱体 | (600,750) | 1200 | a=500,b=100,
c=100 | 100 |
|
Forward model parameters
|
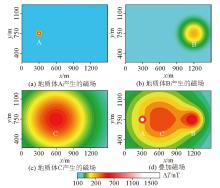
|
The modeled magnetic anomalies
|
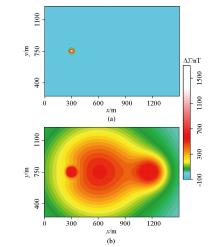
|
The separated residual (a) and regional (b) anomalies by the low-rank decomposition using a balance parameter determined in the previous studies
|
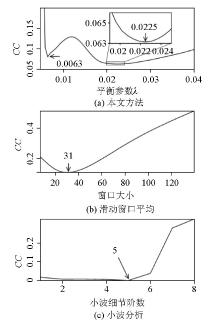
|
The correlation coefficients (CC) between the separated residual and regional fields using different parameters in the mentioned methods
|
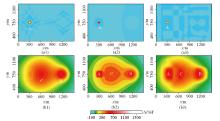
|
The potential field separations using different methods
(a1、b1—the residual anomalies and regional anomalies using the low-rank decomposition with a balance parameter of λ=0.022 5; a2、b2—the residual anomalies and regional anomalies using the sliding window average method with a window size of 31×31; a3、b3—the residual anomalies and regional anomalies using the wavelet analysis method with 5 orders details
|

|
The potential field separations using different methods
(a1、b1—the residual anomalies and regional anomalies using the low-rank decomposition with a balance parameter of λ=0.006 3; a2、b2—the residual anomalies and regional anomalies using the sliding window average method with a window size of 101×101; a3、b3—the residual anomalies and regional anomalies using the wavelet analysis method with 7 orders details)
|
19])
">

|
The separated result of anomalies A, B, and C with different methods(a1、b1、c1—the results using the proposed method; a2、b2、c2 —the results using the sliding window average method; a3、b3、c3—the results using the wavelet analysis method; a4、b4、c4—the results using the method from Zhu et al.[19])
|

| 本文低秩矩阵分解 | 滑动窗口平均 | 小波多尺度分析 | Zhu等[19] | | CC | Err/nT | CC | Err/nT | CC | Err/nT | CC | Err/nT | | 异常A | 0.99 | 30.6 | 0.92 | 201.5 | 0.93 | 131.7 | 0.99 | 64.4 | | 异常B | 0.99 | 21.2 | 0.55 | 226.1 | 0.55 | 171.5 | 0.47 | 201.2 | | 异常C | 1.00 | 29.9 | 0.97 | 110.0 | 0.94 | 109.5 | 0.94 | 198.2 |
|
The correlation coefficients (CC) and the maximum errors (Err) between the separated anomalies and the real anomalies
|

|
Comparison of the separated anomalies A (a), B (b), and C (c) along the profile y=750 m
|
Fig.8a will be used to Fig.11)
">

|
The modeled residual (a), the regional (b), and the total (c) gravity anomalies(P1, P2, and P3 shown in Fig.8a will be used to Fig.11)
|
19])
">

|
The separated residual gravity anomalies (a—the proposed method; b—the sliding window average method; c—the wavelet analysis method; d—the method shown in Zhu et al[19])
|
19])
">

|
The separated regional gravity anomalies(a—the proposed method; b—the sliding window average method; c—the wavelet analysis method; d—the method shown in Zhu et al[19])
|
Fig.8a
">
|
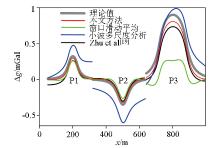
Comparison of the separated anomalies along the profiles P1~P3 as shown in Fig.8a
|
|
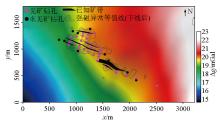
1∶10 000 Bouguer gravity anomaly in the study area covered by the downward continued magnetic anomalies with high values
|
|
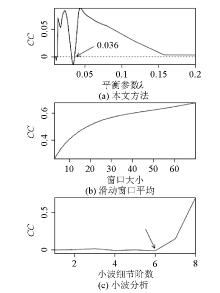
The parameter estimation for the mentioned methods
|
|
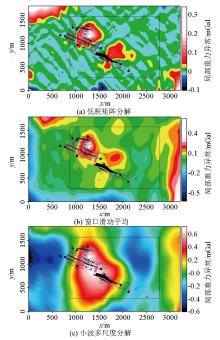
The separated residual gravity anomalies using the mentioned three methods
|

| 低秩矩阵分解 | 滑动窗口平均 | 小波多尺度分析 | | 全区 | 0 | 0.55 | 0.14 | 局部(图14中
黑色线框) | -0.08 | -0.22 | -0.74 |
|
The correlation coefficients (CC) between the separated residual and regional fields using the mentioned methods
|
| [1] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.
|
| [1] |
Guan Z N. Geomagnetic field and magnetic exploration[M]. Beijing: Geological Publishing House, 2005.
|
| [2] |
曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005.
|
| [2] |
Zeng H L. Gravity field and gravity exploration[M]. Beijing: Geological Publishing House, 2005.
|
| [3] |
王正科, 卢琳, 刘花婷. 一种实测重力异常区域场的消除方法[J]. 物探与化探, 2021, 45(6):1569-1577.
|
| [3] |
Wang Z K, Lu L, Liu H T. A way of eliminating the regional field of measured gravity anomalies[J]. Geophysical and Geochemical Exploration, 2021, 45(6):1569-1577.
|
| [4] |
赵文举, 赵荔, 杨战军, 等. 插值切割位场分离方法改进及其在资料处理中的应用[J]. 物探与化探, 2020, 44(4):886-893.
|
| [4] |
Zhao W J, Zhao L, Yang Z J, et al. The improvement of the interpolation cutting potential field separation method and its application to data processing[J]. Geophysical and Geochemical Exploration, 2020, 44(4):886-893.
|
| [5] |
高秀鹤, 于长春, 李行素, 等. 深源矿致异常提取方法对比及应用:以山东齐河—禹城地区航磁数据为例[J]. 现代地质, 2024, 38(1):25-34.
|
| [5] |
Gao X H, Yu C C, Li X S, et al. Comparison and application of extraction methods for aeromagnetic anomaly caused by deep magnetite:A case study of the Qihe-Yucheng ore area,Shandong[J]. Geoscience, 2024, 38(1):25-34.
|
| [6] |
于炳飞, 罗恒, 李端, 等. 金牛火山岩盆地重磁异常综合分析及找矿预测[J]. 地质科技通报, 2021, 41(3):282-299.
|
| [6] |
Yu B F, Luo H, Li D, et al. Comprehensive analysis of gravity and magnetic anomalies in Jinniu volcanic basin for prediction of ore deposits[J]. Bulletin of Geological Science and Technology, 2021, 41(3):282-299.
|
| [7] |
孙争, 王俊, 丁鹏, 等. 一种重力异常向上延拓高度最优化确定方法[J]. 物探与化探, 2023, 47(1):162-170.
|
| [7] |
Sun Z, Wang J, Ding P, et al. Amethod for determining the optimal height for upward continuation of gravity anomalies[J]. Geophysical and Geochemical Exploration, 2023, 47(1):162-170.
|
| [8] |
褚伟, 徐亚, 郝天珧. 基于球面重力反演苏拉威西地区莫霍面结构[J]. 地球物理学报, 2022, 65(6):2198-2209.
|
| [8] |
Chu W, Xu Y, Hao T Y. Moho structure in Sulawesi area based on spherical gravity inversion[J]. Chinese Journal of Geophysics, 2022, 65(6):2198-2209.
|
| [9] |
任朗宁. 二连盆地位场数据处理与构造解释[D]. 长春: 吉林大学, 2019.
|
| [9] |
Ren L N. Data processing and structural interpretation of the potential field in Erlian Basin[D]. Changchun: Jilin University, 2019.
|
| [10] |
陈国军. 频率域滤波在重力异常分离中的研究及应用[D]. 成都: 成都理工大学, 2017.
|
| [10] |
Chen G J. The research and application of frequency domain filtering in gravity anomaly separation[D]. Chengdu: Chengdu University of Technology, 2017.
|
| [11] |
刘天佑, 吴招才, 詹应林, 等. 磁异常小波多尺度分解及危机矿山的深部找矿:以大冶铁矿为例[J]. 地球科学—中国地质大学学报, 2007, 32(1):135-140.
|
| [11] |
Liu T Y, Wu Z C, Zhan Y L, et al. Wavelet multi-scale decomposition of magnetic anomaly and its application in searching for deep-buried minerals in crisis mines:A case study from Daye iron mines[J]. Earth Science—Journal of China University of Geosciences, 2007, 32(1):135-140.
|
| [12] |
孟庆奎, 张文志, 高维, 等. 重力位场小波多尺度分解性质的分析与应用[J]. 物探与化探, 2022, 46(4):946-954.
|
| [12] |
Meng Q K, Zhang W Z, Gao W, et al. Property analysis and application of multi-scale wavelet decomposition of gravity potential field[J]. Geophysical and Geochemical Exploration, 2022, 46(4):946-954.
|
| [13] |
陈召曦. 位场数据的曲波变换与信息提取应用[D]. 北京: 中国地质大学(北京), 2012.
|
| [13] |
Chen Z X. The curvelet Transform and Its Application to Information Extraction for Potential Data[D]. Beijing: China University of Geosciences, 2012.
|
| [14] |
罗潇, 王彦国, 邓居智, 等. 位场异常分离方法的对比分析——以江西相山铀多金属矿田为例[J]. 地球物理学进展, 2017, 32(3):1190-1196.
|
| [14] |
Luo X, Wang Y G, Deng J Z, et al. Comparative analysis on the methods of potential field separation:A case study of the Jiangxi Xiangshan uranium polymetallic orefield[J]. Progress in Geophysics, 2017, 32(3):1190-1196.
|
| [15] |
袁雨欣, 胡婷, 王之洋, 等. 求解二阶解耦弹性波方程的低秩分解法和低秩有限差分法[J]. 地球物理学报, 2018, 61(8):3324-3333.
|
| [15] |
Yuan Y X, Hu T, Wang Z Y, et al. Solving second-order decoupled elastic wave equation using low-rank decomposition and low-rank finite differences[J]. Chinese Journal of Geophyics, 2018, 61(8):3324-3333.
|
| [16] |
Kreimer N, Sacchi M D. A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation[J]. Geophysics, 2012, 77(3):113-122.
|
| [17] |
Anvari R, Kahoo A R, Mohammadi M, et al. Seismic random noise attenuation using sparse low-rank estimation of the signal in the time-frequency domain[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(5):1612-1618.
|
| [18] |
朱丹, 刘天佑, 李宏伟. 利用数据低秩性和稀疏性的位场分离[J]. 石油地球物理勘探, 2019, 54(4):925-936.
|
| [18] |
Zhu D, Liu T Y, Li H W. Potential field separation based on the low rank and sparse characteristics[J]. Oil Geophysical Prospecting, 2019, 54(4):925-936.
|
| [19] |
Zhu D, Li H W, Liu T Y, et al. Low-rank matrix decomposition method for potential field data separation[J]. Geophysics, 2020, 85(1):G1-G16.
|
| [20] |
朱丹. 基于矩阵低秩分解理论的位场数据处理方法研究[D]. 武汉: 中国地质大学, 2020.
|
| [20] |
Zhu D. Research on potential field data processing based on low-rank matrix decomposition theory[D]. Wuhan: China University of Geosciences, 2020.
|
| [21] |
彭义刚, 索津莉, 戴琼海, 等. 从压缩传感到低秩矩阵恢复:理论与应用[J]. 自动化学报, 2013, 39(7):981-994.
|
| [21] |
Peng Y G, Suo J L, Dai Q H, et al. From compressed sensing to low-rank matrix recovery:Theory and applications[J]. Acta Automatica Sinica, 2013, 39(7):981-994.
|
| [22] |
杨秀红, 苟田坤, 薛怡, 等. 结合稀疏先验与多模式分解的低秩张量恢复方法[J]. 中国图象图形学报, 2024, 29(4):0922-0938
|
| [22] |
Yang X H, Gou T K, Xue Y, et al. Low-rank tensor recovery using sparse prior and multi-modal tensor factorization[J]. Journal of Image and Graphics, 2024, 29(4):0922-0938
|
| [23] |
徐望明, 邢华松, 方顺, 等. 基于自适应加权低秩矩阵恢复的图像去噪[J]. 华中科技大学学报:自然科学版, 2023, 51(11):83-90.
|
| [23] |
Xu W M, Xing H S, Fang S, et al., Image denoising based on adaptive weighted low-rank matrix recovery[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2023, 51(11):83-90.
|
| [24] |
Chandrasekaran V, Sanghavi S, Parrilo P A, et al. Rank-sparsity incoherence for matrix decomposition[J]. SIAM Journal on Optimization, 2009, 21(2):572-596.
|
| [25] |
Lin Z C, Chen M M, Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. Mathematical Programming, 2010, 181(2):116-127.
|
| [26] |
胡静, 陶洋. 基于RPCA的群稀疏表示人脸识别方法[J]. 重庆邮电大学学报:自然科学版, 2020, 32(3):459-468.
|
| [26] |
Hu J, Tao Y. Group sparse representation face recognition method based on RPCA[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2020, 32(3):459-468.
|
| [27] |
胡静, 陶洋, 郭坦, 等. 基于低秩矩阵恢复的群稀疏表示人脸识别方法[J]. 计算机工程与设计, 2019, 40(12):3588-3593.
|
| [27] |
Hu J, Tao Y, Guo T, et al. Face recognition method by group sparse representation and low rank recovery[J]. Computer Engineering and Design, 2019, 40(12):3588-3593.
|
| [28] |
黄志强. 基于低秩表达的图像去噪算法研究[D]. 武汉: 武汉大学, 2018.
|
| [28] |
Huang Z Q. Research on low rank representation for image denoising[D]. Wuhan: Wuhan University, 2018.
|
| [29] |
郝儒儒. 基于矩阵分解的低秩张量恢复算法及其应用[D]. 大连: 大连理工大学, 2017.
|
| [29] |
Hao R R. Matrix decomposition based low-rank tensor recovery algorithm and its application[D]. Dalian: Dalian University of Technology, 2017.
|
| [30] |
Yu M, Dick J M, Mao J W, et al. Ilvaite as a thermodynamic recorder of multistage retrograde alteration in large Galinge skarn Fe deposit,Western China[J]. Journal of Central South University, 2019, 26(12):3534-3550.
|
| [31] |
宋双, 张恒磊, 向下延拓在深部矿产勘探中的应用———以青海某矿区为例[J]. 物探与化探. 2014, 38 (6):1195-1199
|
| [31] |
Song S., Zhang H.L. The Application of downward continuation to deep mineral exploration:A case study of an ore distrist in QingHai Province[J]. Geophysical and Geochemical Exploration, 2014, 38 (6):1195-1199
|
| [32] |
朱朝吉, 周肇武, 刘天佑, 等. 高精度磁测找矿效果:以青海尕林格矿区为例[J]. 地质与勘探, 2011, 47(2):277-283.
|
| [32] |
Zhu C J, Zhou Z W, Liu T Y, et al. Application of high-precision magnetic survey to prospecting:A case study in the Galinge deposit of Qinghai Province[J]. Geology and Exploration, 2011, 47(2):277-283.
|
| [33] |
王彦国, 田野, 邓居智, 等. 基于噪声扰动下重力二阶垂向导数与归一化磁源强度的重磁相关性分析——以相山铀矿田为例[J]. 石油地球物理勘探, 2023, 58(5):1231-1243.
|
| [33] |
Wang Y G, Tian Y, Deng J Z, et al. Gravity and magnetic correlation analysis based on the second-order vertical derivative of gravity anomaly and normalized source strength of magnetic anomaly with noise disturbance:A case of Xiangshan uranium orefields[J]. Oil Geophysical Prospecting, 2023, 58(5):1231-1243.
|
|
|
|

