信号自适应识别多道反褶积方法

doi:10.11720/wtyht.2024.1497

Abstract
Figure/Table
References
Related Citation (15)

Download: PDF (7987 KB) HTML (1 KB)
Export: BibTeX | EndNote (RIS)

Abstract

Deconvolution plays a critical role in enhancing the resolution of seismic data.However,conventional deconvolution methods, though boosting the high-frequency components of seismic signals,amplify the energy of high-frequency noise,thereby reducing the signal-to-noise ratios(SNRs) of seismic records after deconvolution.The contradiction between resolution and SNRs restricts the ability of existing deconvolution methods to characterize thin-layer structures.Hence,this study proposed a multi-channel deconvolution method for self-adaptive signal recognition.The method extracted seismic signal recognition operators from raw seismic data.It introduced them as spatial regularization constraints into the objective function of multi-channel deconvolution,somewhat achieving high-resolution processing with self-adaptive signal recognition capabilities.Based on the spatial predictability of seismic signals,their recognition operators were estimated and extracted directly from seismic data,demonstrating high adaptability to seismic records.As indicated by the test analysis of the model and actual data,the proposed method can effectively suppress the amplification effect of high-frequency noise during deconvolution,thus improving resolution and maintaining the SNRs of seismic records.

Key words： deconvolution signal recognition high resolution seismic data

Received: 25 January 2024 Published: 08 January 2025

ZTFLH:

P631.4

	Service

	E-mail this article
	Add to my bookshelf
	Add to citation manager
	E-mail Alert
	RSS
	Articles by authors
	Jian-Lei ZHANG
	Peng-Fei WANG
	Yun-Song SUN
	Guo-Fa LI

Cite this article:

Jian-Lei ZHANG,Peng-Fei WANG,Yun-Song SUN, et al. A multi-channel deconvolution method for self-adaptive signal recognition[J]. Geophysical and Geochemical Exploration, 2024, 48(6): 1702-1708.

URL:

https://www.wutanyuhuatan.com/EN/10.11720/wtyht.2024.1497 OR https://www.wutanyuhuatan.com/EN/Y2024/V48/I6/1702

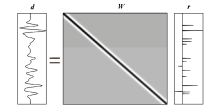
Schematic diagram of convolution process

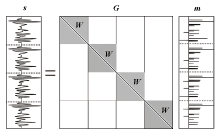
Principle of multi-channel convolution

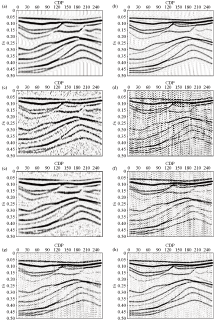
Synthetic seismic data deconvolution results
a—noiseless synthetic seismic data;b—noiseless single channel deconvolution results;c—synthetic seismic data with a SNR of -1 dB;d—single channel deconvolution results affected by noise;e—seismic data after denoising;f—deconvolution of denoised data;g—de-noising the deconvolution results;h—signal adaptive recognition multi-channel deconvolution results

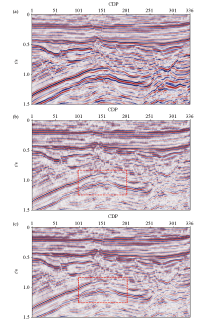
Field seismic data deconvolution results
a—initial seismic data;b—single channel deconvolution result;c—reflection structure constrained multichannel deconvolution result

Local comparison of results processed by different methods
a—local processing results of single channel deconvolution;b—reflection structure constrained multichannel deconvolution local processing results

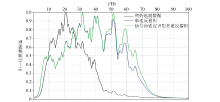
Amplitude spectra of results from different methods

[1]	Lines L R, Ulrych T J. The old and the new in seismic deconvolution and wavelet estimation[J]. Geophysical Prospecting, 1977, 25(3):512-540.
[2]	Oldenburg D W, Scheuer T, Levy S. Recovery of the acoustic impedance from reflection seismograms[J]. Geophysics, 1983, 48(10):1318-1337.
[3]	Yuan S Y, Wang S X. Influence of inaccurate wavelet phase estimation on seismic inversion[J]. Applied Geophysics, 2011, 8(1):48-59.
[4]	Berkhout A J. Least-squares inverse filtering and wavelet deconvolution[J]. Geophysics, 1977, 42(7):1369-1383.
[5]	Cooke D A, Schneider W A. Generalized linear inversion of reflection seismic data[J]. Geophysics, 1983, 48(6):665-676.
[6]	Zhang R, Sen M K, Srinivasan S. Multi-trace basis pursuit inversion with spatial regularization[J]. Journal of Geophysics and Engineering, 2013, 10(3):035012.
[7]	Ma M, Wang S X, Yuan S Y, et al. Multichannel spatially correlated reflectivity inversion using block sparse Bayesian learning[J]. Geophysics, 2017, 82(4):V191-V199.
[8]	Lan T, Liu H, Liu N, et al. Joint inversion of electromagnetic and seismic data based on structural constraints using variational born iteration method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1):436-445.
[9]	Hamid H, Pidlisecky A. Multitrace impedance inversion with lateral constraints[J]. Geophysics, 2015, 80(6):M101-M111.
[10]	Anagaw A Y, Sacchi M D. Edge-preserving seismic imaging using the total variation method[J]. Journal of Geophysics and Engineering, 2012, 9(2):138-146.
[11]	Gholami A. Nonlinear multichannel impedance inversion by total-variation regularization[J]. Geophysics, 2015, 80(5):R217-R224.
[12]	Wang D H, Gao J H. Multichannel seismic impedance inversion with anisotropic total variation regularization[C]// Qingdao:International Geophysical Conference,Society of Exploration Geophysicists and Chinese Petroleum Society, 2017:128.
[13]	Hamid H, Pidlisecky A. Structurally constrained impedance inversion[J]. Interpretation, 2016, 4(4):T577-T589.
[14]	Clapp R G, Biondi B L, Claerbout J F. Incorporating geologic information into reflection tomography[J]. Geophysics, 2004, 69(2):533-546.
[15]	Lelièvre P G, Oldenburg D W. A comprehensive study of including structural orientation information in geophysical inversions[J]. Geophysical Journal International, 2009, 178(2):623-637.
[16]	Zhang Y P, Zhou H, Wang Y F, et al. A novel multichannel seismic deconvolution method via structure-oriented regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60:5910410.
[17]	Pereg D, Cohen I, Vassiliou A A. Multichannel sparse spike inversion[J]. Journal of Geophysics and Engineering, 2017, 14(5):1290-1299.
[18]	McNamara D E. Ambient noise levels in the continental United States[J]. Bulletin of the Seismological Society of America, 2004, 94(4):1517-1527.
[19]	Anvari R, Nazari Siahsar M A, Gholtashi S, et al. Seismic random noise attenuation using synchrosqueezed wavelet transform and low-rank signal matrix approximation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(11):6574-6581.
[20]	Fomel S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6):1946-1960.
[21]	Canales L L. Random noise reduction[C]// SEG Technical Program Expanded Abstracts,Society of Exploration Geophysicists, 1984:329.
[22]	Claerbout J F, Robinson E A. The error in least-squares inverse filtering[J]. Geophysics, 1964, 29(1):118-120.
[23]	Abma R, Claerbout J. Lateral prediction for noise attenuation by t-x and f-x techniques[J]. Geophysics, 1997, 60(6):1887-1896.
[24]	Claerbout J. Multidimensional recursive filters via a helix[J]. Geophysics, 1998, 63(5):1532-1541.