|
|
|
| Seismic impedance optimization inversion combining model inversion with deep learning inversion |
HUANG Wen-Lu( ), YAN Jian-Guo, REN Li-Long, XIE Rui ), YAN Jian-Guo, REN Li-Long, XIE Rui |
| College of Geophysics, Chengdu University of Technology, Chengdu 610059, China |
|
|
|
|
Abstract Based on the combination ofdata- and model-driven approaches, this study expanded the labels of the training set through model inversion results, and added the model inversion objective function to the deep learning algorithm. By constructing a new loss function, this study proposed a seismic impedance optimization inversion method combining model inversion with deep learning inversion. The semi-supervised deep learning network inversion under a pseudo-label was achieved using the RNN network structure. The network inversion results were used as the initial model to participate in the model inversion. The final optimization inversion was completed by continuous iterative optimization of both network and model inversion. The method proposed in this study proves to possess high inversion accuracy and practicability, as demonstrated by the synthesis of the Marmousi model and the actual data.
|
|
Received: 07 July 2023
Published: 19 September 2024
|
|
|
|
|
|
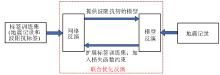
|
Schematic of the optimized inversion process
|
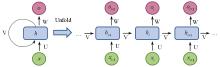
|
Schematic of RNN structure
|
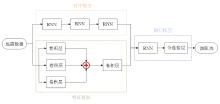
|
Schematic of wave impedance inversion network structure based on deep learning
|
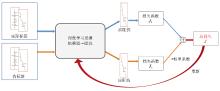
|
Optimize the loss function composition of the inversion
|
|
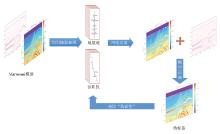
Schematic of how pseudo-labels are generated
|
|
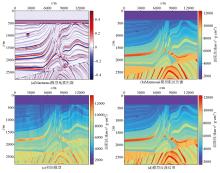
The initial model of model inversion and the results of the inversion
|
|
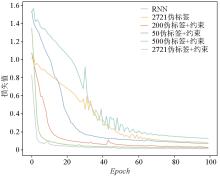
Decline of the loss function
|
|
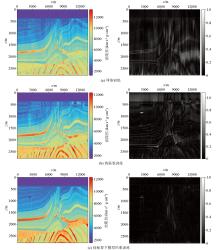
Prediction results(left) and error rate(right) of different inversion methods
|
|
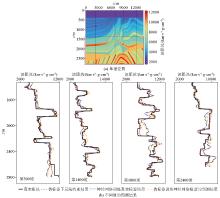
Single trace prediction results of network models with different inversion methods
|

| RNN | 伪标签 | 伪标签+
反演约束 | | 第500道
相对 第1400道
误差 第1800道
第2400道 | 0.1296 | 0.1176 | 0.0547 | | | 0.0671 | 0.0722 | 0.0490 | | | 0.0988 | 0.1054 | 0.0493 | | | 0.0877 | 0.0827 | 0.0441 | | | MSE | 0.0616 | 0.0573 | 0.0158 | | | R2 | 0.9378 | 0.9415 | 0.9839 | |
|
Evaluation effect of the relative error of one trace in the prediction results of different inversion methods
|

|
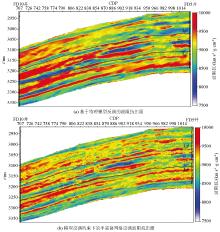
Connecting well profile in the research area
|
|
Comparison of inversion results based on different inversion methods
|
| [1] |
Chen Y K, Chen H M, Xiang K, et al. Geological structure guided well log interpolation for high-fidelity full waveform inversion[J]. Geophysical Journal International, 2016, 207(2):1313-1331.
|
| [2] |
王华忠, 王雄文, 王西文. 地震波反演的基本问题分析[J]. 岩性油气藏, 2012, 24(6):1-9.
|
| [2] |
Wang H Z, Wang X W, Wang X W. Analysis of the basic problems of seismic wave inversion[J]. Lithologic Reservoirs, 2012, 24(6):1-9.
|
| [3] |
蒋星达, 张伟, 杨辉. 地球物理反演问题中的贝叶斯方法研究[J]. 地球与行星物理论评, 2022, 53(2):159-171.
|
| [3] |
Jiang X D, Zhang W, Yang H. The research on Bayesian inference for geophysical inversion[J]. Reviews of Geophysics and Planetary Physics, 2022, 53(2):159-171.
|
| [4] |
邢文军, 曹思远, 陈思远, 等. 基于谱反演方法的叠后纵波阻抗反演[J]. 物探与化探, 2023, 47(2):429-437.
|
| [4] |
Xing W J, Cao S Y, Chen S Y, et al. Post-stack P-wave impedance inversion based on spectral inversion[J]. Geophysical and Geochemical Exploration, 2023, 47(2):429-437.
|
| [5] |
凡友华, 刘雪峰, 陈晓非. 面波频散反演地下层状结构的拟牛顿法[J]. 物探与化探, 2006, 30(5):456-459.
|
| [5] |
Fan Y H, Liu X F, Chen X F. The quasi Newton method in the inversion of the dispersion curve of Rayleigh wave in multilayered media[J]. Geophysical and Geochemical Exploration, 2006, 30(5):456-459.
|
| [6] |
Reichstein M, Camps-Valls G, Stevens B, et al. Deep learning and process understanding for data-driven Earth system science[J]. Nature, 2019, 566:195-204.
|
| [7] |
Yu S W, Ma J W. Deep learning for geophysics:Current and future trends[J]. Reviews of Geophysics, 2021, 59(3):1-36.
|
| [8] |
肖立志. 机器学习数据驱动与机理模型融合及可解释性问题[J]. 石油物探, 2022, 61(2):205-212.
|
| [8] |
Xiao L Z. The fusion of data-driven machine learning with mechanism models and interpretability issues[J]. Geophysical Prospecting for Petroleum, 2022, 61(2):205-212.
|
| [9] |
Das V, Pollack A, Wollner U, et al. Convolutional neural network for seismic impedance inversion[J]. Geophysics, 2019, 84(6):R869-R880.
|
| [10] |
Alfarraj M, AlRegib G. Semisupervised sequence modeling for elastic impedance inversion[J]. Interpretation, 2019, 7(3):SE237-SE249.
|
| [11] |
Biswas R, Sen M K, Das V, et al. Prestack and poststack inversion using a physics-guided convolutional neural network[J]. Interpretation, 2019, 7(3):SE161-SE174.
|
| [12] |
Luo R, Chen H Z, Wang B F. Semisupervised seismic impedance inversion with data augmentation and uncertainty analysis[J]. Geophysics, 2023, 88(4):M213-M224.
|
| [13] |
Su Y Q, Cao D P, Liu S Y, et al. Seismic impedance inversion based on deep learning with geophysical constraints[J]. Geoenergy Science and Engineering, 2023, 225:211671.
|
| [14] |
王蓉, 熊杰, 刘倩, 等. 基于深度神经网络的重力异常反演[J]. 物探与化探, 2022, 46(2):451-458.
|
| [14] |
Wang R, Xiong J, Liu Q, et al. Inversion of gravity anomalies based on a deep neural network[J]. Geophysical and Geochemical Exploration, 2022, 46(2):451-458.
|
| [15] |
吴嵩, 宁晓斌, 杨庭伟, 等. 基于神经网络的探地雷达数据去噪[J]. 物探与化探, 2023, 47(5):1298-1306.
|
| [15] |
Wu S, Ning X B, Yang T W, et al. Neural network-based denoising for ground-penetrating radar data[J]. Geophysical and Geochemical Exploration, 2023, 47(5):1298-1306.
|
| [16] |
卞保力. 基于高密度三维地震河道砂体储层预测方法研究与应用[D]. 成都: 成都理工大学, 2019.
|
| [16] |
Bian B L. Research and application of reservoir prediction method of channel sands based on high density three-dimensional seismic data[D]. Chengdu: Chengdu University of Technology, 2019.
|
| [1] |
WANG Kang, LIU Cai-Yun, XIONG Jie, WANG Yong-Chang, HU Huan-Fa, KANG Jia-Shuai. Seismic wave impedance inversion based on the fully convolutional residual shrinkage network[J]. Geophysical and Geochemical Exploration, 2023, 47(6): 1538-1546. |
| [2] |
HU Wei-Guang, BO Yong, YI Xiao-Lin, XIAO Wei, YOU Sai-Ke, DIAO Zhuo-Nan. A TENTATIVE DISCUSSION ON THE RECOGNITION OF BIOHERMIN YUANBA AREA, EASTERN SICHUANPROVINCE[J]. Geophysical and Geochemical Exploration, 2010, 34(5): 635-642. |
|
|
|
|

