|
|
|
| Fractal model-based 2.5 D finite element modeling of complex resistivity method |
Long Xiu-Jie1( ), Chen Han-Bo2( ), Chen Han-Bo2( ), Mo Ya-Jun1, Ou Xiao-Yi1, Lu Sheng-Hui1 ), Mo Ya-Jun1, Ou Xiao-Yi1, Lu Sheng-Hui1 |
1. Guangxi Geophysical Investigation Institute,Liuzhou 545005,China
2. College of Earth Sciences, Guilin University of Technology,Guilin 541006,China |
|
|
|
|
Abstract This study proposed the variational problem of 2.5D finite element forward modeling of the complex resistivity method and detailed the process of solving stiff matrix of finite equations. The Fractal model was introduced as a research model for studying the equivalent induced polarization anomalies of spectra. Furthermore, the complex conductivity and complex potential of a grid unit were linearly interpolated. Then, to obtain anomalous complex potential, finite element linear equations were solved using the biconjugate gradient stabilized method with incomplete LU decomposition. The results of three typical geoelectric models validated the correctness and accuracy of the algorithm proposed in this study. Furthermore, this study analyzed the abnormal response characteristics of 2.5D complex resistivity under different frequencies.
|
|
Received: 09 July 2021
Published: 17 August 2022
|
|
|
|
Corresponding Authors:
Chen Han-Bo
E-mail: 496178747@qq.com;chenhanbo@glut.edu.cn
|
|
|
|

|
The amplitude (a) and phase (b) of complex resistivity for different frequency exponent
|
|
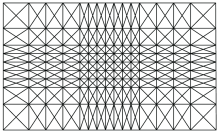
Sketch of finite element mesh
|
|
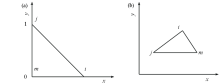
Parent element (a) and sub-element(b) of linear interpolation
|

| n | h/m | ρ0/(Ω·m) | m | δr | τ/μs | τf/ms | η | τ0/ps | 1
2 | 5
∞ | 100
10 | 0.906
0.885 | 4.959
4.877 | 23.43
18.72 | 10
100 | 0.20
0.44 | 1.0
1.0 |
|
parameters of the first model
|
|
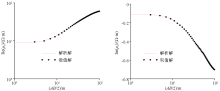
Comparison of 2.5D FEM result with numerical filter wave numerical solution
|

|
Cross section of second model
|

| Kind | ρ0/(Ω·m) | m | δr | τ/μs | τf/ms | η | τ0/ps | 半空间
异常体 | 5200
1470 | 0.906
0.885 | 4.959
4.877 | 23.43
18.72 | 10
100 | 0.20
0.44 | 1.0
1.0 |
|
Fractal parameters of the second model
|
|
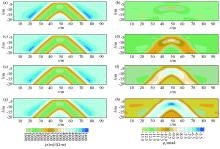
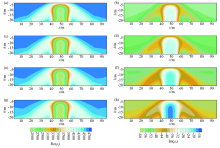
The pseudo section of amplitude and phase of apparent complex resistivity in dipole-dipole array for giving the frequencies
|
|
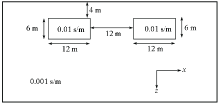
The pseudo section of real and imaginary component of apparent complex resistivity in four-pole array for giving the frequencies
|
|
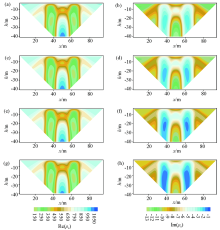
Cross section of second model
|

| Kind | ρ0/
(Ω·m) | m | δr | τ/μs | τf/ms | η | τ0/ps | | 半空间 | 1000 | 0.906 | 4.959 | 23.43 | 10 | 0.20 | 1.0 | 异常体
(左) | 100 | 0.885 | 4.877 | 18.72 | 100 | 0.44 | 1.0 | 异常体
(右) | 100 | 0.885 | 4.877 | 18.72 | 100 | 0.44 | 1.0 |
|
Fractal parameters of the second model
|
|
The pseudo section of real and imaginary component of apparent complex resistivity in four-pole array for giving the frequencies
|
|
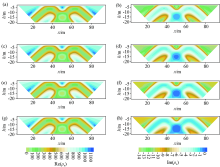
The pseudo section of real and imaginary component of apparent complex resistivity in dipole-dipole array for giving the frequencies
|
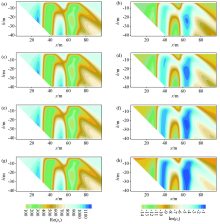
|
The pseudo section of real and imaginary component of apparent complex resistivity in pole-dipole array for giving the frequencies
|
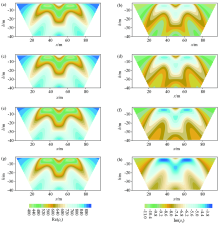
|
The pseudo section of real and imaginary component of apparent complex resistivity in pole-pole array for giving the frequencies
|
| [1] |
杨振威, 郑伟, 李晓斌, 等. 频谱激电法的发展与展望[J]. 物探与化探, 2015, 39(1):22-28.
|
| [1] |
Yang Z W, Zhen W, Li X B, et al. The development and prospect of the spectral induced polarization method[J]. Geophysical and Geochemical Exploration, 2015, 39(1):22-28.
|
| [2] |
罗延钟, 张桂青. 频率域激电法原理[M]. 北京: 地质出版社, 1988.
|
| [2] |
Luo Y Z, Zhang G Q. Principle of frequency domain IP method[M]. Beijing: Geological Publishing House, 1988.
|
| [3] |
罗延钟, 方胜. 视复电阻率频谱的一种近似反演方法[J]. 地球科学, 1986, 11(1) : 9-102.
|
| [3] |
Luo Y Z, Fang S. An approximate invrtsion of the apparent complex resistivity spectrum[J]. Earth Science, 1986, 11(1) : 9-102.
|
| [4] |
张桂青, 崔先文, 罗延钟. 一种反演频谱激电法视频谱求取真参数的方法[J]. 地质与勘探, 1987, 23(4) : 48-54.
|
| [4] |
Zhang G Q, Cui X W, Luo Y Z. The Determination of intrinsic parameters by inversing IP apparent spectrum[J]. Geology and Exploration, 1987, 23(4) : 48-54.
|
| [5] |
刘崧, 官善友, 高鹏飞. 求极化椭球体真 Cole-Cole 参数的联合谱激电反演[J]. 地球物理学报, 1994, 37(S1) : 542-551.
|
| [5] |
Liu S, Guan S Y, Gao P F. Joint sip inversion for estimation of intrinsiccole-cole parameters of apolarizable ellipsoid[J]. Chinese Journal of Geophysice, 1994, 37(S1) : 542-551.
|
| [6] |
Hohmann G W. Three-dimensional induced polarization and electromagnetic modelling[J]. Geophysics, 1975, 40 (2) :309-324.

|
| [7] |
Weller A, Seichter M, Kampke A. Induced-polarization modelling using complex electrical conductivities[J]. Geophys. J. Int., 1996, 127(1):387-398.

|
| [8] |
Oldenburg D W, Li Y. Inversion of induced polarization data[J]. Geophysics, 1994, 59 (9) :1327-1341.

|
| [9] |
Rocha B R P, Habashy T M. Fractal geometry, porosity and complex resistivity. I: From rough pore interfaces to hand specimens, in: Developments in Petrophysics[M], London: Geological Society Publishing House, London, 1995.
|
| [10] |
柳建新, 蒋鹏飞, 童孝忠, 等. 不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J]. 中南大学学报:自然科学版, 2009, 40(2):484 -491.
|
| [10] |
Liu J X, Jiang P F, Tong X Z, et al. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of Central South University: Science and Technology, 2009, 40(2):484 -491.
|
| [1] |
ZENG Bo, LIU Shuo, YANG Jun, FENG De-Shan, YUAN Zhong-Ming, LIU Jie, WANG Xun. Influence of surface undulations on GPR-based underground pipeline detection[J]. Geophysical and Geochemical Exploration, 2023, 47(4): 1064-1070. |
| [2] |
YANG Tian-Chun, HU Feng-Ming, YU Xi, FU Guo-Hong, LI Jun, YANG Zhui. Analysis and application of the responses of the frequency selection method of telluric electricity field[J]. Geophysical and Geochemical Exploration, 2023, 47(4): 1010-1017. |
|
|
|
|

