|
|
|
| Density interface inversion method in spherical coordinates and its application in the South China mainland |
WANG Xiang1,2( ), GUO Liang-Hui1 ), GUO Liang-Hui1 |
1.School of Geophysics and Information Technology, China University of Geosciences (Beijing), Beijing 100083, China
2.Kunming Natural Resources Comprehensive Survey Center of China Geological Survey, Kunming 650000, China |
|
|
|
|
Abstract The density interface inversion method has been playing an important role in the oil and gas exploration, regional structure inference studies as well as crustal crystal basement surface and Moho undulations researches. Most of the density interface inversion methods are generally based on the Cartesian coordinate system. When large regional or even global scale data are dealt with, the influence of earth curvature cannot be ignored, and the density interface inversion method based on Tesseroid model of spherical coordinate system needs to be considered. However, due to the limitations of calculation accuracy and efficiency, the existing density interface inversion method based on Tesseroid cannot be well applicable to the surface gravity observation data. In this paper, on the basis of previous studies, a density interface inversion method of spherical coordinate system suitable for surface observation data is proposed. Firstly, the gravity Gauss-Legendre integral formula in the spherical coordinate system is simplified to improve the forward calculation efficiency. Then, an optimized adaptive subdivision algorithm is introduced to enhance the calculation accuracy. According to the previous forward calculation and by using Cordell iterative optimization algorithm, the authors propose a density interface inversion method for the surface observation data in the spherical coordinate system. The proposed inversion method in this paper can be verified through the synthetic data test. The inversion results show that the proposed method can overcome the limitation of calculating precision and efficiency of the surface observation data. In addition, the inversion results based on spherical coordinate system are better than those based on cartesian coordinate system. Finally, tests on real data from South China mainland verify the feasibility of the presented methods. The results show that Moho depth rises gradually from the west to the east, with the western part uplifting dramatically and the eastern part uplifting gently. Between Wuling Mountain and Guizhou-Guangxi border, there is an obvious NNE-Moho step.
|
|
Received: 17 February 2020
Published: 26 October 2020
|
|
|
|
|
|
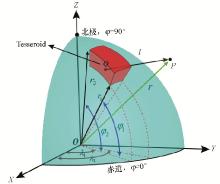
|
The sketch of Tesseroid model
|
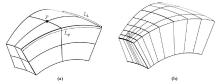
|
Sketch of discretization of Tesseroid
a—routine discretization shown that the tesseroid had a uniform division. Lφ, Lλ are the dimensions of the tesseroid’s top surface;b—adaptive discretization shown that a fine division of the tesseroid close the computation point and a coarser division further away
|
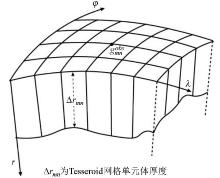
|
The forward model of tesseroid
|
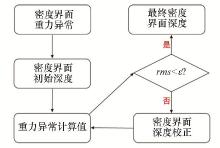
|
The flow chart for Cordell iterative approach
|
|
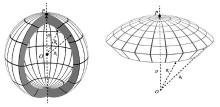
The images of spherical shell models
a—inside view of a shell;b—side view of a shell
|
|
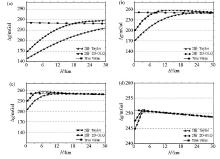
The gravity anomaly calculated by the Taylor on the different cell size and 2D-GLQ methods based on the different height of observation surface
|

|
The improvement of efficiency of computation by using the method of this paper
a—the Briggs logarithm of Er based on the different value of nφ and nλ;b—the changing trend of T1/T2 when Er get reduced
|

|
The depth of academic interface and its forward result
a—the density interface model graph; b— the gravity anomaly graph of density interface model forward result by the GQL-Plus method of this paper
|
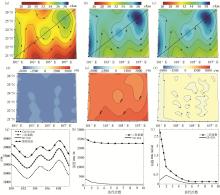
Figure 8(b)
a—Cartesian coordinates;b—two order Taylor;c—2D-GLQ inversion results; d,e,f—respectively are errors of (a), (b), and (c); g—shown the diagonal section comparisons of (a), (b) and (c);h—depth RMS;i—bouguer RMS
">
|
Comparisons of the inversion results from the data of Figure 8(b)
a—Cartesian coordinates;b—two order Taylor;c—2D-GLQ inversion results; d,e,f—respectively are errors of (a), (b), and (c); g—shown the diagonal section comparisons of (a), (b) and (c);h—depth RMS;i—bouguer RMS
|
39];g—The difference of (c) and (e)
">
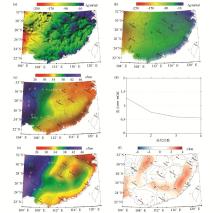
|
Comparisons of the inversion results from measured data in South China
a— The Bouguer anomaly in South China;b—The Moho gravity anomaly in South China by using the low-pass filter;c—The Moho depth in South China by the inversion method of this paper;d—The trend chart of depth RMS;f—The Moho depth in South China[39];g—The difference of (c) and (e)
|
| [1] |
孙德梅, 闵志. 三维密度界面反演的一个近似方法[J]. 物探与化探, 1984,8(2):89-98.

|
| [1] |
Sun D M, Min Z. A technique for approximate inversion of three-dimensional density interface[J]. Geophysical and Geochemical Exploration, 1984,8(2):89-98.

|
| [2] |
Cordell L, Henderson R G. Iterative three-dimensional solution of gravity anomaly data using a digital computer[J]. Geophysics, 1968,33(4):596-601.

|
| [3] |
Silva J B C. Interactive gravity inversion[J]. Geophysics, 2006: 1-9.
|
| [4] |
Zhou X. Gravity inversion of 2D bedrock topography for heterogeneous sedimentary basins based on line integral and maximum difference reduction method[J]. Geophysical Prospecting, 2013,61(1):220-234.

|
| [5] |
Silva J B C, Santos D F, Gomes K P. Fast gravity inversion of basement relief[J]. Geophysics, 2014,79(5):79-91.
|
| [6] |
刘元龙, 王谦身. 用压缩质面法反演重力资料以估算地壳构造[J]. 地球物理学报, 1977,20(1):59-69.
|
| [6] |
Liu Y L, Wang Q S. Inversion of gravity data by use of a method of “compressed mass plane” to estimate crustal structure[J]. Chinese J. Geophys. , 1977,20(1):59-69.
|
| [7] |
江为为, 周立宏, 肖敦清, 等. 东北地区重磁场与地壳结构特征[J]. 地球物理学进展, 2006,21(3):730-738.

|
| [7] |
Jiang W W, Zhou L H, Xiao D Q, et al. The characteristics of crust structure and the gravity and magnetic fields in northeast region of China[J]. Progress in Geophysics, 2006,21(3):730-738.
|
| [8] |
胡立天, 郝天珧. 带控制点的三维密度界面反演方法[J]. 地球物理学进展, 2014,29(6):2498-2503.

|
| [8] |
Hu L T, Hao T Y. The inversion of three-dimensional density interface with control points[J]. Progress in Geophysics, 2014,29(6):2498-2503.

|
| [9] |
Marquardt D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963,11(2):431-441.

|
| [10] |
Chakravarthi V, Sastry S R. GUI based inversion code for automatic quantification of strike limited listric fault sources and regional gravity background from observed bouguer gravity anomalies[J]. Journal Geological Society of India, 2014,83:625-638.
|
| [11] |
Mojica O F, Bassrei A. Regularization parameter selection in the 3D gravity inversion of the basement relief using GCV: A parallel approach[J]. Computers and Geosciences, 2015,82:205-213.

|
| [12] |
关小平. 利用Parker公式反演界面的一种有效方法[J]. 物探化探计算技术, 1991,13(3):236-242.
|
| [12] |
Guan X P. An effective and simple approach of subsurface inversion using Parker’s equation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1991,13(3):236-242.
|
| [13] |
Parker R L. The rapid calculation of potential anomalies[J]. Geophysical Journal Royal Astronomical Society, 1972,37(3):447-455.

|
| [14] |
Oldenburg D W. The inversion and interpretation of gravity anomalies[J]. Geophysics, 1974,39:526-536.

|
| [15] |
Granser H. Three-dimensional interpretation of gravity data from sedimentary basins using an exponential density-depth function[J]. Geophysical Prospecting, 1987,35(9):1030-1041.
|
| [16] |
Guspi F. Noniterative nonlinear gravity inversion[J]. Geophysics, 1993,58(7):935-940.

|
| [17] |
Santos D F, Silva J B C, Martins C M, et al. Efficient gravity inversion of discontinuous basement relief[J]. Geophysics, 2015,80(4):95-106.
|
| [18] |
Shi L, Li Y H, Zhang E H. A new approach for density contrast interface inversion based on the parabolic density function in the frequency domain[J]. Journal of Applied Geophysics, 2015,116:1-9.

|
| [19] |
Asgharzadeh M F, Von Frese R R B, Kim H R, et al. Spherical prism gravity effects by Gauss-Legendre quadrature integration[J]. Geophys. J. Int, 2007,169:1-11.

|
| [20] |
Heck B, Seitz K. A comparison of the Tesseroid prism and pointmass approaches for mass reductions in gravity field modelling[J]. J. Geod., 2007,81(2):121-136.

|
| [21] |
Roussel C, Verdun J, Cali J, et al. Complete gravity field of an ellipsoidal prism by Gauss-Legendre quadrature[J]. Geophys. J. Int., 2015,203:2220-2236.

|
| [22] |
Uieda L, Barbosa V C F, Braitenberg C. Tesseroids: Forward-modeling gravitational fields in spherical coordinates[J]. Geophysics, 2016: 41-48.
|
| [23] |
Uieda L, Barbosa V C F. Fast nonlinear gravity inversion in spherical coordinates with application to the South American Moho[J]. Geophys. J. Int., 2017,208:162-176.

|
| [24] |
Anderson E G. The effect of topography on solutions of stokes' problem[M]. School of Surveying, University of New South Wales, Kensington, NSW, Australia, 1976.
|
| [25] |
Liang Q, Chen C, Li Y. 3-Dinversion of gravity data in spherical coordinates with application to the GRAIL data[J]. J. Geophys. Res. Planets, 2014,119:1359-1373.

|
| [26] |
Zhang Y, Wu Y L, Yan J G, et al. 3D inversion of full gravity gradient tensor data in spherical coordinate system using local north oriented frame[J]. Earth, Planets and Space, 2018,70(58):1-23.

|
| [27] |
梁青. 月球重力异常特征与三维密度成像研究:[D]. 武汉:中国地质大学(武汉), 2010.
|
| [27] |
Liang Q. Gravity anomaly features and 3D density imaging of the moon: [D]. Wuhan:China University of Geosciences (Wuhan), 2010.
|
| [28] |
Wild-Pfeiffer F. A comparison of different mass elements for use in gravity gradiometry[J]. J Geod., 2008,82:637-653.

|
| [29] |
Grombein T, Seitz K, Heck B. Optimized formulas for the gravitational field of a Tesseroid[J]. J. Geodesy, 2013,87:645-660.

|
| [30] |
Shen W B, Deng X L. Evaluation of the fourth-order tesseroid formula and new combination approach to precisely determine gravitational potential[J]. Stud. Geophys. Geod, 2016,60:1. (DOI: 10.1007/s11200-016-0402-y).

|
| [31] |
Guo L H, Shi L, Meng X H, et al. Apparent magnetization mapping in the presence of strong remanent magnetization: The space-domain inversion approach[J]. Geophysics, 2015,81(2):J11-J24.

|
| [32] |
Li Z, Hao T, Xu Y, et al. An efficient and adaptive approach for modeling gravity effects in spherical coordinates[J]. Journal of Applied Geophysics, 2011,73(3):221-231.

|
| [33] |
Bott M H P. The use of rapid digital computing methods for direct gravity interpretation of sedimentary basin[J]. Geophysical Journal Royal Astronomical Society, 1960,3:63-67.

|
| [34] |
Heiskanen W A, Moritz H. Physical geodesy[M]. San Francisco:Freeman, 1967.
|
| [35] |
Vaníček P, Novák P, Martinec Z. Geoid, topography, and the Bouguer plate or shell[J]. J. Geodesy, 2001,75:210-215.

|
| [36] |
Karcol R. Gravitational attraction and potential of spherical shell with radially dependent density[J]. Stud. Geophys. Geod., 2011,55:21-34.

|
| [37] |
舒良树. 华南构造演化的基本特征[J]. 地质通报, 2012,31(7):1035-1053.
|
| [37] |
Shu L S. An analysis of principal features of tectonic evolution in South China Block[J]. Geological Bulletin of China, 2012,31(7):1035-1053.
|
| [38] |
张国伟, 郭安林, 王岳军, 等. 中国华南大陆构造与问题[J]. 中国科学:地球科学, 2013,43(10):1553-1582.
|
| [38] |
Zhang G W, Guo A L, Wang Y J, et al. Tectonics of South China continent and its implications[J]. Science China: Earth Sciences, 2013,43(10):1553-1582.

|
| [39] |
郭良辉, 孟小红, 石磊, 等. 优化滤波方法及其在中国大陆布格重力异常数据处理中的应用[J]. 地球物理学报, 2012,55(12):4078-4088.

|
| [39] |
Guo L H, Meng X H, Shi L, et al. Preferential filtering method and its application to Bouguer gravity anomaly of Chinese continent[J]. Chinese J. Geophys. , 2012,55(12):4078-4088.
|
| [40] |
Hilde T W C, Uyeda S, Kroenke L. Evolution of the western Pacific and its margin[J]. Tectonophysics, 1977,38:145-165.

|
| [41] |
Smith A D. A plate model for Jurassic to recent intraplate volcanism in the Pacific Ocean basin[G]// Foulger G R, Jurdy D M. Plates, plumes, and planetary processes. Geol Soc Am (Spec Papers), 2007,430:471-495.
|
|
|
|

