|
|
|
| A study of fractal singular value decomposition method for controlling factors of coal seam thickness |
Ya-Nan SUN1, Xing LIU2( ), Zhi-Gen ZHAO1 ), Zhi-Gen ZHAO1 |
1. Survey School, Anhui University of Science and Technology, Huainan 232000, China
2. Earth and Environment School, Anhui University of Science and Technology, Huainan 232000, China |
|
|
|
|
Abstract The thickness distribution of coal seams results from the combined control of various geological factors, and the control factors of coal are different in different regions. Previous studies have focused on qualitative comparative analysis, and hence it is very difficult for them to identify accurately the control factors and their distribution. In this study, according to the multi-fractal characteristics and the generalized self-similarity principle of the coal seam thickness spatial distribution, the authors transformed coal seam thickness into feature space and performed singular value decomposition. Based on the fractal law of energy measure and energy spectral density,the authors used the least squares method to fit singular value decomposition figure into multipul lines, determined different inflection points, selected the singular value and the corresponding feature subspace in the first three sections for reconstruction, compared anomalies after reconstruction with various variables that affect the thickness of coal seams, extracted various implicit geological factors for coal control, and thus realized the quantitative analysis of controlling factors of coal seam thickness. The authors analyzed the No. 8 main coal seam in Panji coal mine (peripheral) of Huainan as a study case, detected the fact that the main control factors for the thickness of coal seam in this area are ancient terrain, same sedimentary structure and hydrodynamic conditions in ancient geography, and compared the results with the control factors obtained by the corresponding analysis. The results show the effectiveness of this method in quantitative analysis.
|
|
Received: 09 April 2019
Published: 28 November 2019
|
|
|
|
Corresponding Authors:
Xing LIU
E-mail: 2268190319@qq.com
|
|
|
|
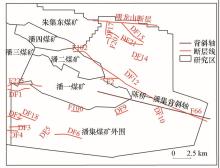
|
Geological map of Panji coal mine(peripheral)
|
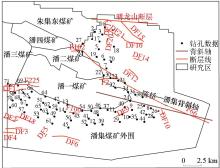
|
Distribution map of 71 drilling points
|

| 平均值 | 最小值 | 最大值 | 标准差 | 变异系数 | 偏度 | 峰度 | Sig. | | 2.28 | 0.55 | 6.48 | 0.97 | 42.54 | 1.71 | 4.70 | 0.056 |
|
The result of K-S normal test
|
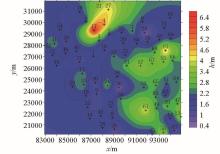
|
The equivalent figure of M8H
|
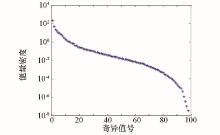
|
The figure of M8H singular value with energy density
|
|
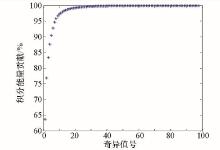
The M8H integral energy contribution figure of singular values
|

|
M8H figure of fractal singular value decomposition
|
|
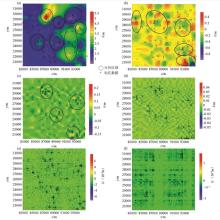
The anomaly figure of M8H
a—anomaly reconstruction of first segment singular value and corresponding subspace;b—anomaly reconstruction of second segment singular value and corresponding subspace;c—anomaly reconstruction of third segment singular value and corresponding subspace;d—anomaly reconstruction of fourth segment singular value and corresponding subspace;e—anomaly reconstruction of fifth segment singular value and corresponding subspace;f—anomaly reconstruction of sixth segment singular value and corresponding subspace
|
|
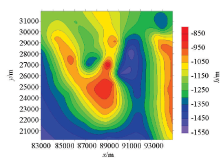
The equivalent figure of M8DG
|
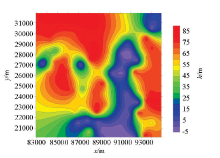
|
The equivalent figure of SXH
|
|
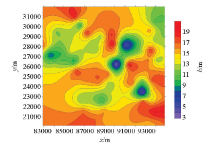
The equivalent figure of XSHZH
|
|
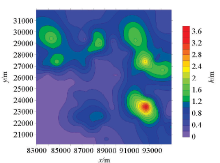
The equivalent figure of XSHZYB
|

| SXH | XSHZH | XSHZYB | M8DG | M8H | | SXH | 1.000 | 0.309 | -0.175 | 0.635 | 0.206 | | XSHZH | 0.309 | 1.000 | -0.298 | 0.238 | 0.233 | | XSHZYB | -0.175 | -0.298 | 1.000 | -0.128 | 0.090 | | M8DG | 0.635 | 0.238 | -0.128 | 1.000 | -0.046 | | M8H | 0.206 | 0.233 | 0.090 | -0.046 | 1.000 |
|
Correlation between variables
|

| 成分1 | 成分2 | | SXH | 0.867 | -0.140 | | XSHZH | 0.240 | -0.659 | | XSHZYB | -0.047 | 0.896 | | M8DG | 0.921 | -0.072 | | M8H | 0.020 | 0.047 |
|
Composition matrix of coal thickness in the first section
|

| 成分1 | 成分2 | | SXH | 0.880 | 0.129 | | XSHZH | 0.332 | 0.704 | | XSHZYB | -0.194 | -0.591 | | M8DG | 0.870 | 0.064 | | M8H | -0.236 | 0.712 |
|
Composition matrix of coal thickness in the second section
|

| 成分1 | 成分2 | | SXH | 0.871 | 0.168 | | XSHZH | 0.303 | 0.724 | | XSHZYB | -0.182 | -0.560 | | M8DG | 0.890 | 0.049 | | M8H | -0.152 | 0.673 |
|
Composition matrix of coal thickness in the third section
|
| [1] |
刘程, 李向东, 杨守国 . 地质构造对煤层厚度的影响研究[J]. 煤矿安全, 2008 ( 5):14-16.
|
| [1] |
Liu C, Li X D, Yang S G . Study on influence of geologic structure on coal seam thickness[J]. Safe in Coal Minesty, 2008,( 5):14-16.
|
| [2] |
李聪聪, 孙顺新, 张光超 , 等. 滇东北上二叠统可采煤层变化规律及控制因素[J]. 中国地质, 2014,41(6):2110-2121.
|
| [2] |
Li C C, Sun S X, Zhang G C , et al. Variation regularity and control factors of the Upper Permian mineable coal seams in northeastern Yunnan Province[J]. Geology in China, 2014,41(6):2110-2121.
|
| [3] |
刘衡秋, 刘钦甫, 彭苏萍 , 等. 淮南煤田第四含煤段砂体的演化特征及对煤层厚度的控制[J]. 煤田地质与勘探, 2005,33(1):7-10.
|
| [3] |
Liu H Q, Liu Q F, Peng S P , et al. Evolvement characteristic of sand bodies in the fourth coal-bearing interval and its control on coal thickness, Huainan coalfield[J]. Coal Geology & Exploration, 2005,33(1):7-10.
|
| [4] |
刘星 . 煤炭资源空间分布分形特征和厚度变化规律分形滤波方法研究[J]. 金属矿山, 2017(10):81-88.
|
| [4] |
Liu X . Fractal Character of Coal Resources Distribution and the Spatial Distribution Law of Coal Thickness based on S-A method[J]. Metal Mine, 2017 ( 10):81-88.
|
| [5] |
曹代勇, 刘钦甫, 彭苏萍 , 等. 超化井田二1煤层厚度变化规律定量研究[J]. 煤田地质与勘探, 1998,26(5):28-32.
|
| [5] |
Cao D Y, Liu Q F, Peng S P , et al. Quantitative analysis on the thickness variation of NO.2-1 coal seam in chaohua mine field[J]. Coal Geology & Exploration, 1998,26(5):28-32.
|
| [6] |
夏玉成, 胡克兴 . 对应分析在控煤因素研究中的应用[J]. 西安矿业学院学报, 1986,37(3):60-65.
|
| [6] |
Xia Y C, Hu K X . Application of correspondence analysis in the study of coal control factors[J]. Journal of Xi’an University of Science & Technology, 1986,37(3):60-65.
|
| [7] |
李庆谋, 成秋明. 分形奇异(特征)值分解方法与地球物理和地球化学异常重建[J]. 地球学报:中国地质大学学报, 2004,29(1):109-118.
|
| [7] |
Li Q M, Cheng Q M . Fractal singular-value (egin-value) decomposition method for geophysical and geochemical anomaly reconstruction[J]. Earth Science:Journal of China University of Geosciences, 2004,29(1):109-118.
|
| [8] |
成秋明 . 多重分形与地质统计学方法用于勘查地球化学异常空间结构和奇异性分析[J]. 地球科学:中国地质大学学报, 2001,26(2):161-166.
|
| [8] |
Cheng Q M . Multifractal and geostatistic methods for characterizing local structure and singularity properties of exploration geochemical anomalies[J]. Earth Science : JournaI of China University of Geosciences, 2001,26(2):161-166.
|
| [9] |
Zuo R G, Cheng Q M, Agterberg F P , et al. Application of singularity mapping technique to identification of loacal anomalies using stream sediment geochemical data, a case study from Gangdese, Tibet, western China[J]. Journal of Geochemical Exploration, 2009,101:225-235.
|
| [10] |
成秋明 . 成矿过程奇异性与矿床多重分形分布[J]. 矿物岩石地球化学通报, 2008,27(3):298-305.
|
| [10] |
Cheng Q M . Singularity of mineralization and multifractal distribution of mineral deposits[J]. BuIletin of Mineralogy,Petrology and Geochemistry, 2008,27(3):298-305.
|
| [11] |
Cheng Q M . Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas[J]. Journal of Geochemical Exploration, 2012,122:55-70.
|
| [12] |
康春玉, 章新华 . 一种基于奇异值分解的自适应降噪方法[J]. 声学技术, 2008,27(3):455-458.
|
| [12] |
Kang C Y, Zhang X H . An adaptive noise reduction method based Oil singularity value decompose[J]. Technical Acoustics, 2008,27(3):455-458.
|
| [13] |
邢琮琮, 吴燕冈, 赵昕 , 等. 奇异值分解 (SVD)在位场数据去噪中的应用[J]. 世界地质, 2016,35(4):1119-1126.
|
| [13] |
Xing C C, Wu Y G, Zhao X , et al. Application of singular value decomposition (SVD) de-noising in potential field data[J]. Global Geology, 2016,35(4):1119-1126.
|
| [14] |
唐步尧, 李智勇, 孙星明 . 一种基于奇异值量化的鲁棒性水印算法[J]. 计算机工程与应用, 2006,( 26):63-67.
|
| [14] |
Tang B Y, Li Z Y, Sun X M . Robust watermarking algorithm based on quantization of sigular value[J]. Computer Engineering and Applications, 2006,( 26):63-67.
|
| [15] |
李志星, 石博强 . 自适应奇异值分解的随机共振提取微弱故障特征[J]. 农业工程学报, 2017,33(11):60-67.
|
| [15] |
Li Z X, Shi B Q . Extracting weak fault characteristics with adaptive singular value decomposition and stochastic resonance[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017,33(11):60-67.
|
| [16] |
于海征 . 基于奇异值分解的数字图像的特征提取[J]. 工程数学学报, 2004,21(8):131-134.
|
| [16] |
Yu H Z . Feature extraction of digital Image on singular value decomposition[J]. Chinese Journal of Engineering Mathematics, 2004,21(8):131-134.
|
| [17] |
陆红艳 . 基于奇异值分解与稀疏表示的人脸识别方法[D]. 南京:南京邮电大学, 2014.
|
| [17] |
Lu H Y . Face recognition based on image sparse representation and singular value decomposition[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2014.
|
| [18] |
卜军, 沈书豪, 谢焰 . 潘集深部勘查区山西组煤层发育及顶底板工程地质特征[J]. 中国煤炭地质, 2017,29(8):43-47.
|
| [18] |
Bu J, Shen S H, Xie Y . Shanxi formation coal seam development and roof,floor engineering geological features in Panji coalmine deep part exploration area[J]. Coal Geology of China, 2017,29(8):43-47.
|
| [19] |
郭鹏飞 . 淮南潘集深部13-1煤层孔隙结构特征分析[D]. 淮南:安徽理工大学, 2017.
|
| [19] |
Guo P F . Study on pore structure characteristics of deep-seated coal seal No.13-1 from Panji Huainan area[D]. Huainan: Anhui University Of Science & Technology, 2017.
|
| [20] |
刘会虎, 兰天贺, 胡宝林 , 等. 淮南潘集外围深部煤层气地球化学特征及成因[J]. 煤炭学报, 2018,43(2):498-506.
|
| [20] |
Liu H H, Lan T H, Hu B L , et al. Geochemical characteristics and its origins of CBM in deep-seated coal seam around Panji mining area of Huainan[J]. Journal of China Coal Society, 2018,43(2):498-506.
|
| [21] |
张小军, 陶明信, 王万春 , 等. 淮南潘集、张集煤矿次生生物气地球化学特征[J]. 天然气工业, 2008,28(7):34-38.
|
| [21] |
Zhang X J, Tao M X, Wang W C , et al. Geochemical behaviors of secondary biogas in Panji and Zhangji coal mines in Huainan coal field[J]. Natural Gas Industry, 2008,28(7):34-38.
|
| [22] |
李庆谋, 刘少华 . GIS环境下地球物理信号的奇异值分解、多维分形特征与应用[J]. 地球物理学进展, 2003,18(1):97-102.
|
| [22] |
Li Q M, Liu S H . Geophysical signal decomposition by singular method and application in GIS[J]. Progress in Geophysics, 2003,18(1):97-102.
|
| [23] |
周顶, 陈永清, 赵彬彬 . 奇异值分解技术及地球化学块体方法在南黄岗—甘珠尔庙成矿带找矿中的应用[J]. 中国地质, 2014,41(2):621-637.
|
| [23] |
Zhou D, Chen Y Q, Zhao B B . The application of singular-Value decomposition (SVD) and geochemical blocks methods to the prospecting in southern Huanggang—Ganzhu’ermiao metalLogenic belt[J]. Geology in China, 2014,41(2):621-637.
|
| [24] |
刘霞, 王运锋 . 基于最小二乘法的自动分段多项式曲线拟合方法研究[J]. 科学技术与工程, 2014,14(3):55-58.
|
| [24] |
Liu X, Wang Y F . Research of automatically piecewise polynomial curve-fitting method based on least-square principle[J]. Science TechnoIogy and Engineering, 2014,14(3):55-58.
|
| [25] |
李晓晖, 袁峰, 贾蔡 , 等. 基于反距离加权和克里金插值的S-A多重分形滤波对比研究[J]. 测绘科学, 2012,37(3):87-89.
|
| [25] |
Li X H, Yuan F, Jia C , et al. Contrastive study of S-A multifractal filtering method based on inverse distance weighted and Kriging interpolation[J]. Science of Surveying and Mapping, 2012,37(3):87-89.
|
| [1] |
Jiu-Qiang JIN, Jin-Long WANG, Gang-Yi XIAO, Jian LI, Mao-Sheng DENG, Zhi-Bo WANG, Jiu-Ming JIANG, Qi WANG, Xin WANG, Sheng-Bo GENG. Airborne gamma ray spectrum mapping effects with NASVD de-noising[J]. Geophysical and Geochemical Exploration, 2018, 42(4): 817-824. |
| [2] |
SU Shi-Long, HE Zheng-Hua, LIU Yu-Lian, ZHANG Hui, GU Yan-Bin, GUO Wei. The impact of explosive excitation weight on the quality of seismic data analysis in city exploration and countermeasures:A case study of CY City in an oilfield of eastern China[J]. Geophysical and Geochemical Exploration, 2015, 39(6): 1160-1166. |
|
|
|
|

