|
|
|
| Seismic surface wave interpolation method based on optimistic wavelet basis |
| Zhi-Nong WANG1, Cheng-Yu SUN1, Dun-Shi WU2 |
1. School of Geosciences,China University of Petroleum,Qingdao 266580,China
2. PetroChina Research Institute of Petroleum Exploration and Development-Northwest,Lanzhou 730020,China |
|
|
|
|
Abstract The surface wave in the real seismic data can be used to invert near surface shear velocity.If the trace interval is large and the spatial sampling rate is not enough,there will be spatial aliasing.This can not only decrease the signal-to-noise ratio of frequency-velocity spectra but also affect the accuracy of dispersion curves and the result of inversion.So it is necessary to do the interpolation of surface wave.This paper presents a seismic surface wave interpolation method based on optimistic wavelet basis.The optimistic wavelet basis bior6.8 which is suitable for interpolation processing can be selected among many wavelet bases commonly used in seismic data processing through the theoretical analysis and the comparison of experimental error.The use of optimistic wavelet basis bior6.8 will increase the accuracy of interpolation.Because the events of surface wave are linear and the slopes of them are larger,this paper uses the linear normal moveout to level the events of surface wave firstly,then carries out the wavelet transform interpolation,and finally uses the inverse linear normal moveout to recover the surface wave.The effectiveness of the proposed method is verified by the interpolation result of theoretical model and real seismic data.After the interpolation,the waveform of the interpolated surface wave records is well recovered. It can improve the signal-to-noise ratio of frequency-velocity spectra,and solve the aliasing problem effectively caused by the undersampling of the surface wave data.
|
|
Received: 04 June 2018
Published: 20 February 2019
|
|
|
|
Corresponding Authors:
Cheng-Yu SUN
|
|
|
|

|
Sketch of second level wavelet transform
|
|
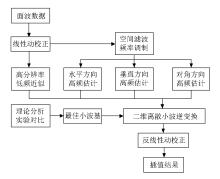
Flow chart of surface wave interpolation
|
|
Interpolation result using optimistic wavelet basis bior6.8
a—original record;b—track record;c—interpolation record;d—interpolation error
|

|
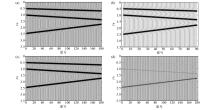
Interpolation error comparison
a—db wavelet basis error;b—sym wavelet basis error;c—bior wavelet basis error
|

|
Wavelet basis bior6.8
a—decomposition of scaling function;b—decomposition of wavelet function;c—reconstruction of scaling function;d—reconstruction of wavelet function
|

|
Filters corresponding to wavelet basis bior6.8
a—decomposition low pass filter;b—decomposition high pass filter;c—reconstructing low pass filter;d—reconstructing high pass filter
|
|
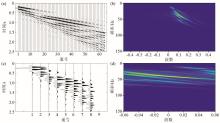
Seismic records and dispersive images before and after extracting traces
a—original record;b—frequency wavenumber spectrum corresponding to the original record;c—track record;d—frequency wavenumber spectrum corresponding to the track record
|

|
Four sub-bands used in 2D wavelet inverse transformation
a—low frequency approximation part;b—high frequency estimation of horizontal direction;c—high frequency estimation of vertical direction;d—high frequency estimation of diagonal direction
|

|
Interpolation result and its FK spectrum
a—interpolation results;b—frequency wavenumber spectrum
|
|
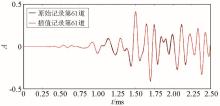
The 61st trace waveform comparison between original record and interpolation result
|

|
Dispersion images comparison
a—frequency velocity spectrum of original recording;b—frequency velocity spectrum of track recording;c—frequency velocity spectrum of interpolation results
|
|
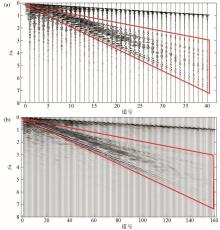
Seismic records before and after interpolation
a—original record;b—interpolation results
|

|
Dispersion images comparison
a—frequency velocity spectrum of original recording;b—frequency velocity spectrum of interpolation results
|
| [1] |
Park C B, Miller R D, Xia J . Multichannel analysis of surface waves[J]. Geophysics, 1999,64(3):800-808.

|
| [2] |
Socco L V, Foti S, Boier O D . Surface-wave analysis for building near-surface velocity models-established approaches and new perspectives[J]. Geophysics, 2010,75(5):A83-A102.
|
| [3] |
伍敦仕, 孙成禹, 林美言 . 基于频率—速度域多重信号分类的面波高分辨率频散成像方法[J]. 石油物探, 2017,56(1):141-149.

|
| [3] |
Wu D S, Sun C Y, Lin M Y . High resolution dispersion imaging of surface waves based on signal classification in frequency-velocity domain[J]. Geophysical Prospecting for Petroleum, 2017,56(1):141-149.
|
| [4] |
夏江海, 高玲利, 潘雨迪 , 等. 高频面波方法的若干新进展[J]. 地球物理学报, 2015,58(8):2591-2605.

|
| [4] |
Xia J H, Gao L L, Pan Y D , et al. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 2015,58(8):2591-2605.
|
| [5] |
姜福豪, 李培明, 张翊孟 , 等. 多道面波频散分析在实际大炮数据中的应用[J]. 石油地球物理勘探, 2018,53(1):17-24.

|
| [5] |
Jiang F H, Li P M, Zhang Y M , et al. Frequency dispersion analysis of MASW in real seismic data[J]. Oil Geophysical Prospecting, 2018,53(1):17-24.
|
| [6] |
国九英, 周兴元, 俞寿朋 . F-X域等道距道内插[J]. 石油地球物理勘探, 1996,31(1):28-34.

|
| [6] |
Guo J Y, Zhou X Y, Yu S P . Iso-interval trace interpolation in F-X domain[J]. Oil Geophysical Prospecting, 1996,31(1):28-34.
|
| [7] |
国九英, 周兴元 . F-K域等道距道内插[J]. 石油地球物理勘探, 1996,31(2):211-218.
|
| [7] |
Guo J Y, Zhou X Y . Iso-spaced trace interpolation in F-K domain[J]. Oil Geophysical Prospecting, 1996,31(2):211-218.
|
| [8] |
周聪, 刘江平, 曾祥芝 , 等. 小波变换在面波插值中的应用[J]. 中南大学学报:自然科学版, 2012,43(11):4395-4403.
|
| [8] |
Zhou C, Liu J P, Zeng X Z , et al. Application of wave transform on Rayleigh wave onterpolation[J]. Journal of Central South University:Science and Technology, 2012,43(11):4395-4403.
|
| [9] |
李庆忠 . 地震信号内插与噪声剔除(一)[J]. 地球物理学报, 1987,30(5):514-531.
|
| [9] |
Li Q Z . Seismic signal interpolation and noise deletion(1)[J]. Chinese Journal of Geophysics, 1987,30(5):514-531.
|
| [10] |
李庆忠 . 地震信号内插与噪声剔除(二)[J]. 地球物理学报, 1988,31(3):329-341.

|
| [10] |
Li Q Z . Seismic signal interpolation and noise deletion(2)[J]. Chinese Journal of Geophysics, 1988,31(3):329-341.
|
| [11] |
Spitz S . Seismic trace interpolation in the f-x domain[J]. Geophysics, 1991,56(6):785-794.

|
| [12] |
Wang Z L, Li Y D. Trace interpolation using wavelet transform [C]//Expanded Abstracts of the 64 th Annual SEG Meeting.Los Angles:Society of Exploration Geophysicists , 1994,13:729-730.
|
| [13] |
Hindriks C O H, Schonewille M A, Duijndam A J W. Efficient reconstruction of irregularly sampled seismic data in two dimensions [C]//The 58 th Conference of the EAGE , 1996.
|
| [14] |
Duijndam A J W, Schonewille M A, Hindriks C O H . Reconstruction of band-limited signals,irregularly sampled along one spatial direction[J]. Geophysics, 1999,64(2):524-538.

|
| [15] |
高静怀, 汪文秉, 朱光明 , 等. 地震资料处理中小波函数的选取研究[J]. 地球物理学报, 1996,39(3):392-400.

|
| [15] |
Gao J H, Wang W B, Zhu G M , et al. On the choice of wavelet functions for seismic data processing[J]. Chinese Journal of Geophysics, 1996,39(3):392-400.
|
| [16] |
王西文, 高静怀, 李幼铭 . 高分辨地震资料处理中导数小波函数的构造[J]. 石油物探, 2000,39(2):64-71.

|
| [16] |
Wang X W, Gao J H, Li Y M . Construction of derivative wavelet function in high resolution seismic data processing[J]. Geophysical Prospecting for Petroleum, 2000,39(2):64-71.
|
| [17] |
王西文, 刘全新, 高静怀 , 等. 地震资料在小波域的分频处理与重构[J]. 石油地球物理勘探, 2001,36(1):78-85.

|
| [17] |
Wang X W, Liu Q X, Gao J H , et al. Frequency-shared processing and reconstitution of seismic data in wavelet domain[J]. Oil Geophysical Prospecting, 2001,36(1):78-85.
|
| [18] |
Porsani M J . Seismic trace interpolation using half-step prediction filters[J]. Geophysics, 1999,64(5):1461-1467.

|
| [19] |
Herrmann F. Optimal seismic imaging with curvelets [C]//Expanded Abstracts of the 69 th Annual SEG Meeting,Society of Exploration Geophysicists , 2003.
|
| [20] |
Herrmann F. Curvelet imaging and processing:an overview [C]//CSEG National Convention, 2004.
|
| [21] |
Hennenfent G, Herrmann F, Neelamani R. Sparseness-constrained seismic deconvolution with curvelets [C]//CSEG Annual Conference Proceedings, 2005.
|
| [22] |
Candes E, Demanet L, Donoho D . Fast discrete curvelet transforms[J]. Multiscale Modeling and Simulation, 2006,5(3):861-899.

|
| [23] |
Donoho D . Compressed sensing[J]. IEEE Transactions on Information Theory, 2006,52(4):1289-1306.

|
| [24] |
张华, 陈小宏, 杨海燕 . 地震信号去噪的最优小波基选取方法[J]. 石油地球物理勘探, 2011,46(1):70-75.

|
| [24] |
Zhang H, Chen X H, Yang H Y . Optimistic wavelet basis selection in seismic signal noise elimination[J]. Oil Geophysical Prospecting, 2011,46(1):70-75.
|
| [25] |
Nazari Siahsar M A, Gholtashi S, Abolghasemi V , et al. Simultaneous denoising and interpolation of 2D seismic data using data-driven non-negative dictionary learning[J]. Signal Processing, 2017,6(17):309-321.
|
| [26] |
Kim B, Jeong S, Byun J , et al. An efficient interpolation approach for insufficient 3D field data[J]. Exploration Geophysics, 2018,49(1):58-67.

|
|
|
|
