|
|
|
| Implicit generation of complex geological surface models based on scalar coordinates |
LIU Pei-Gang1( ), YUAN Hao1, XUE Kai-Xin1, LI Zhao-Liang2,3, LI Zong-Min1 ), YUAN Hao1, XUE Kai-Xin1, LI Zhao-Liang2,3, LI Zong-Min1 |
1. College of Computer Science and Technology, China University of Petroleum (East China), Qingdao 266580, China
2. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China
3. Key Laboratory of Airborne Geophysics and Remote Sensing Geology, Ministry of Land and Resources, Beijing 100083, China |
|
|
|
|
Abstract The construction and presentation of a geological modelprove to be ahot topic and challenge in research on 3D geological modelling. Given the large scale, involvement of complex surfaces, and insufficient geological constraints of geological body data, this study achieved the rapid construction of a large-scale geological surface model using the domain decomposition-based implicit generation method. Initially, implicit functionswere constructed by taking radial basis functions as the kernel functions.Then, the distribution functions of various domainswere solved in parallel usinganoverlapping domain decompositionmethod, reducing the spatiotemporalcost and accelerating the solving process.Subsequently, normal vectors were extracted to generate control pointsand formconstraints on surface fluctuation, thereby effectively controlling the model boundaries. The experimental results indicate that the method proposed in this study can significantly improve the efficiency associated with the solving of distribution functionswhile ensuring the high quality of the model. This study effectively solves the problem of balance between efficiency and precision in geological modeling and provides methodological support for the refinement of geological surfaces.
|
|
Received: 27 December 2023
Published: 22 April 2025
|
|
|
|
|
|
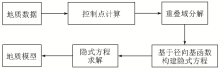
|
Flowchart for model construction
|
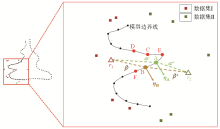
|
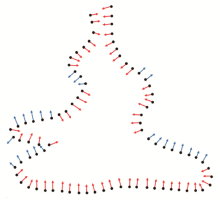
Normal correction method
|
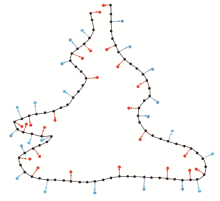
|
2D schematic of control points (red for control points inside the model, blue for control points outside the model)
|
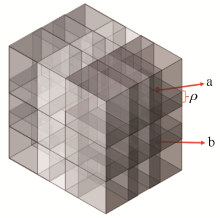
|
Domain overlap
(ρ denotes domain overlap)
|

|
Longitudinal section
|
|
Cross section
|
|
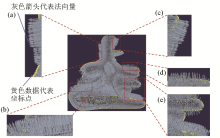
Normal vectors for fixed viewpoints
(a~e represent the amplification effect of the normal vector pointing towards the external area of the model)
|
|
Schematic diagram of normal vector section with fixed viewpoint
|
Fig.7)
">
|
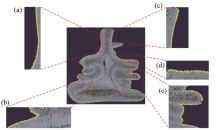
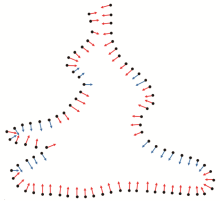
Corrected normal vector
(a~e represent the amplification effect after correcting the normal vector in the corresponding region of Fig.7)
|
|
Schematic diagram of the corrected normal vector section
|
|
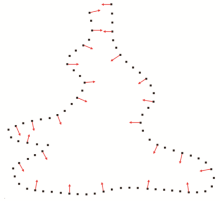
Random selection of normal vectors
(a~e are the region amplification effects of random normal vector screening)
|
|
Schematic of a randomly selected section of a normal vector
|
|
Normal vector extremum selection
(a~e are the region amplification effects of normal vector extremum screening)
|
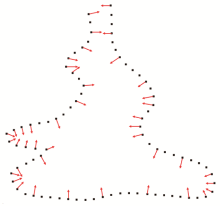
|
Schematic of normal vector extreme value selection cuts
|
|
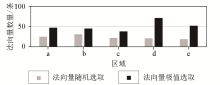
Number of normal vectors in the region of random and extreme selection of normal vectors
|

| 方法 | 矩阵阶数 | | Surfe | (4×N)2 | | 本文方法 | (N/10)2 |
|
Matrix complexity comparison
|

| 方法 | 不同数据量的运行时间 | | 1000 | 3200 | 5000 | 11000 | 50000 | | Surfe | 90 s | 40 min | 2.5 h | 22 h | | 本文方法
(非并行) | 0.91 s | 19.45 s | 29.72 s | 67.58 s | 268.3 s | 本文方法
(并行) | 0.35 s | 3.3 s | 5.2 s | 15.8 s | 120.6 s |
|
Run time comparison
|
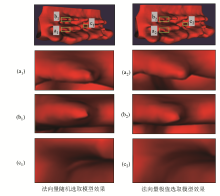
|
Comparison of the results of random and extreme value selection of normal vectors
(a~c are locally enlarged areas)
|

| 参数 | 数据量 | | 1000 | 3200 | 5000 | 11000 | | 运行时间/s | 0.35 | 3.3 | 5.2 | 15.8 | | 平均曲率/10-4 | 8.921 | 4.972 | 3.519 | 1.377 |
|
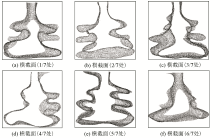
Mean curvature of the model for different data volumes
|
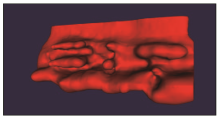
|
Model effect for 1 000 data points
|
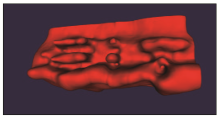
|
Model effect for 3 200 data points
|
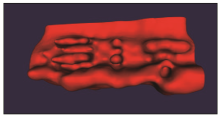
|
Model effect for 5 000 data points
|

|
Model effect for 11 000 data points
|
| [1] |
苗晋祥, 吴继臣, 朱学立, 等. 三维地质建模技术的发展历史与未来展望[G]// 河南地球科学通报2008年卷(下册),河南省地质调查院, 2008.
|
| [2] |
Houlding S. 3D geoscience modeling:Computer techniques for geological characterization[M]. Berlin: Springer-Verlag, 1994.
|
| [3] |
Mallet J L. Discrete modeling for natural objects[J]. Mathematical Geology, 1997, 29(2):199-219.
|
| [4] |
Caumon G, Tertois A L, Zhang L. Elements for stochastic structural perturbation of stratigraphic models[C]// EAGE Conference on Petroleum Geostatistics, 2007.
|
| [5] |
Cherpeau N, Caumon G, Caers J, et al. Method for stochastic inverse modeling of fault geometry and connectivity using flow data[J]. Mathematical Geosciences, 2012, 44(2):147-168.
|
| [6] |
Aydin O, Caers J K. Quantifying structural uncertainty on fault networks using a marked point process within a Bayesian framework[J]. Tectonophysics, 2017, 712:101-124.
|
| [7] |
Grose L, Laurent G, Aillères L, et al. Inversion of structural geology data for fold geometry[J]. Journal of Geophysical Research:Solid Earth, 2018, 123(8):6318-6333.
|
| [8] |
Thornton J M, Mariethoz G, Brunner P. A 3D geological model of a structurally complex Alpine region as a basis for interdisciplinary research[J]. Scientific Data, 2018, 5:180238.
|
| [9] |
Renaudeau J, Irakarama M, Laurent G, et al. Implicit modelling of geological structures:A Cartesian gridmethod handling discontinuities with ghostpoints[C]// WIT Transactions on Engineering Sciences,Boundary Elements and other Mesh Reduction Methods XLI, 2018.
|
| [10] |
Manchuk J G, Deutsch C V. Boundary modeling with moving least squares[J]. Computers & Geosciences, 2019, 126:96-106.
|
| [11] |
Schaaf A, de la Varga M, Wellmann F, et al. Constraining stochastic 3D structural geological models with topology information using approximate Bayesian computation in GemPy 2.1[J]. Geoscientific Model Development, 2021, 14(6):3899-3913.
|
| [12] |
Irakarama M, Laurent G, Renaudeau J, et al. Finite difference implicit structural modeling of geological structures[J]. Mathematical Geosciences, 2021, 53(5):785-808.
|
| [13] |
李兆亮, 王林飞, 熊盛青, 等. 基于轮廓线三维矿体表面重建的一种改进算法[J]. 物探与化探, 2019, 43(1):118-124.
|
| [13] |
Li Z L, Wang L F, Xiong S Q, et al. An improved algorithm for surface reconstruction of 3D orebody based on contour line[J]. Geophysical and Geochemical Exploration, 2019, 43(1):118-124.
|
| [14] |
Fernández O, Munoz J A, Arbués P, et al. Three-dimensional reconstruction of geological surfaces:An example of growth strata and turbidite systems from the Ainsa basin (Pyrenees,Spain)[J]. Bulletin of the American Association of Petroleum Geologists, 2004, 88(8):1049-1068.
|
| [15] |
Perrin M, Zhu B T, Rainaud J F, et al. Knowledge-driven applications for geological modeling[J]. Journal of Petroleum Science and Engineering, 2005, 47(1/2):89-104.
|
| [16] |
Vidal-Royo O, Muñoz J A, Hardy S, et al. Structural evolution of Pico del Águila anticline (External Sierras,southern Pyrenees) derived from sandbox,numerical and 3D structural modelling techniques[J]. Geologica Acta, 2013, 11(1):1-26.
|
| [17] |
Cowan E J, Beatson R K, Fright W R, et al. Rapid Geological Modelling[C]// Australian Institute of Geoscientists,Applied Structural Geology for Mineral Exploration and Mining,International Symposium. Kalgoorlie: 2002.
|
| [18] |
Wilde B J, Deutsch C V. Kriging and simulation in presence of stationary domains:Developments in boundary modeling[M]. Dordrecht: Springer Netherlands, 2012.
|
| [19] |
Wellmann F, Caumon G. 3D Structural geological models:Concepts,methods,and uncertainties[M]. Amsterdam: Elsevier, 2018.
|
| [20] |
李兆亮, 潘懋, 韩大匡, 等. 储层精细构造模型三维网格化技术[J]. 科学技术与工程, 2017, 17(26):36-42.
|
| [20] |
Li Z L, Pan M, Han D K, et al. 3D gridding technology of reservoir fine structure model[J]. Science Technology and Engineering, 2017, 17(26):36-42.
|
| [21] |
Liu X Y, Li A B, Chen H, et al. 3D modeling method for dome structure using digital geological map and DEM[J]. ISPRS International Journal of Geo-Information, 2022, 11(6):339.
|
| [22] |
Lajaunie C, Courrioux G, Manuel L. Foliation fields and 3D cartography in geology:Principles of a method based on potential interpolation[J]. Mathematical Geology, 1997, 29(4):571-584.
|
| [23] |
Frank T, Tertois A L, Mallet J L. 3D-reconstruction of complex geological interfaces from irregularly distributed and noisy point data[J]. Computers & Geosciences, 2007, 33(7):932-943.
|
| [24] |
Calcagno P, Chilès J P, Courrioux G, et al. Geological modelling from field data and geological knowledge Part I.Modelling method coupling 3D potential-field interpolation and geological rules[J]. Physics of the Earth and Planetary Interiors, 2008, 171(1-4):147-157.
|
| [25] |
Caumon G. Towards stochastic time-varying geological modeling[J]. Mathematical Geosciences, 2010, 42(5):555-569.
|
| [26] |
Yang L, Hyde D, Grujic O, et al. Assessing and visualizing uncertainty of 3D geological surfaces using level sets with stochastic motion[J]. Computers & Geosciences, 2019, 122:54-67.
|
| [27] |
Mallet J L. Space-time mathematical framework for sedimentary geology[J]. Mathematical Geology, 2004, 36(1):1-32.
|
| [28] |
Caumon G, Gray G, Antoine C, et al. Three-dimensional implicit stratigraphic model building from remote sensing data on tetrahedral meshes:Theory and application to a regional model of La popa basin,NE Mexico[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3):1613-1621.
|
| [29] |
Hillier M, De Kemp E, Schetselaar E. 3D form line construction by structural field interpolation (SFI) of geologic strike and dip observations[J]. Journal of Structural Geology, 2013, 51:167-179.
|
| [30] |
Ardeshiri-Lajimi S, Yazdani M, Assadi L A. Control of fault lay-out on seismic design of large underground Caverns[J]. Tunnelling and Underground Space Technology, 2015, 50:305-316.
|
| [31] |
Grose L, Ailleres L, Laurent G, et al. LoopStructural 1.0:Time-aware geological modelling[J]. Geoscientific Model Development, 2021, 14(6):3915-3937.
|
| [32] |
Pereira P E C, Rabelo M N, Ribeiro C C, et al. Geological modeling by an indicator Kriging approach applied to a limestone deposit in Indiara city-Goiás[J]. REM-International Engineering Journal, 2017, 70(3):331-337.
|
| [33] |
Hamdi M, Zagrarni M F, Djamai N, et al. 3D geological modeling for complex aquifer system conception and groundwater storage assessment:Case of Sisseb El Alem Nadhour Saouaf basin,northeastern Tunisia[J]. Journal of African Earth Sciences, 2018, 143:178-186.
|
| [34] |
Chen G X, Zhu J, Qiang M Y, et al. Three-dimensional site characterization with borehole data—A case study of Suzhou area[J]. Engineering Geology, 2018, 234:65-82.
|
| [35] |
Zhang Q, Zhu H H. Collaborative 3D geological modeling analysis based on multi-source data standard[J]. Engineering Geology, 2018, 246:233-244.
|
| [36] |
Gonçalves Í G, Kumaira S, Guadagnin F. A machine learning approach to the potential-field method for implicit modeling of geological structures[J]. Computers & Geosciences, 2017, 103:173-182.
|
| [37] |
Tseng Y H, Wang S. Semiautomated building extraction based on CSG model-image fitting[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(2):171-180.
|
| [38] |
Vollgger S A, Cruden A R, Ailleres L, et al. Regional dome evolution and its control on ore-grade distribution:Insights from 3D implicit modelling of the Navachab gold deposit,Namibia[J]. Ore Geology Reviews, 2015, 69:268-284.
|
| [39] |
Wang J M, Zhao H, Bi L, et al. Implicit 3D modeling of ore body from geological boreholes data using Hermite radial basis functions[J]. Minerals, 2018, 8(10):443.
|
| [40] |
Hillier M J, Schetselaar E M, de Kemp E A, et al. Three-dimensional modelling of geological surfaces using generalized interpolation with radial basis functions[J]. Mathematical Geosciences, 2014, 46(8):931-953.
|
| [41] |
Hillier M, de Kemp E, Schetselaar E. Implicitly modelled stratigraphic surfaces using generalized interpolation[C]// AIP Conference Proceedings, 2016.
|
| [42] |
Guo J T, Wu L X, Zhou W H, et al. Towards automatic and topologically consistent 3D regional geological modeling from boundaries and attitudes[J]. ISPRS International Journal of Geo-Information, 2016, 5(2):17.
|
| [43] |
Guo J T, Wu L X, Zhou W H, et al. Section-constrained local geological interface dynamic updating method based on the HRBF surface[J]. Journal of Structural Geology, 2018, 107:64-72.
|
| [44] |
Guo J T, Wang J M, Wu L X, et al. Explicit-implicit-integrated 3D geological modelling approach:A case study of the Xianyan Demolition Volcano (Fujian,China)[J]. Tectonophysics, 2020, 795:228648.
|
| [45] |
Guo J T, Wang X L, Wang J M, et al. Three-dimensional geological modeling and spatial analysis from geotechnical borehole data using an implicit surface and marching tetrahedra algorithm[J]. Engineering Geology, 2021, 284:106047.
|
| [1] |
XU Hai-Hong, HAN Xiao-Feng, YUAN Bing-Qiang, ZHANG Chun-Guan, WANG Bao-Wen, ZHAO Fei, DUAN Rui-Feng. Optimization of interpolation parameters for 1∶50 000 regular distribution gravity data based on radial basis function[J]. Geophysical and Geochemical Exploration, 2021, 45(6): 1539-1552. |
| [2] |
LI Jun-Jie, YAN Jia-Bin. Optimal shape parameters of RPIM for resolving point source two-dimensional variational problem[J]. Geophysical and Geochemical Exploration, 2015, 39(6): 1233-1237. |
|
|
|
|

