|
|
|
| A method for predicting the brittleness and fracture parameters of shale gas reservoirs based on prestack direct inversion |
| SHI Xue-Wen1,2, WANG Chang1,2, ZHANG Dong-Jun1,2, FENG Yan-Wen1,2 |
1. Shale Gas Research Institute, Southwest Oil & Gasfield Company,PetroChina, Chengdu 610051, China
2. Sichuan Key Laboratory of Shale Gas Evaluation and Exploitation, Chengdu 610051, China |
|
|
|
|
Abstract The conventional inversion of anisotropic media is often constrained by assumptions of narrow-angle incidence and weak changes in stratigraphic properties.Moreover,the prediction of rock elastic parameters typically involves linear inversion and indirect fitting,leading to less accurate and reliable inversion results of petrophysical parameters for anisotropic formations.Hence,this study derived the petrophysical models of Young's modulus,Poisson's ratio,and fracture parameters for vertical transverse isotropy(VTI) media.Based on the precise VTI reflection coefficient equation,this study proposed a Bayesian anisotropic nonlinear direct inversion method,constrained by the L1 norm,to predict the brittleness and fracture parameters of shale gas reservoirs through direct inversion.The proposed method yielded satisfactory application results in a study area of shale gas in Southwest China,offering a novel technique for characterizing shale gas reservoirs.
|
|
Received: 22 January 2025
Published: 07 August 2025
|
|
|
|
|
|

| E/GPa | σ | Vp/
(m·s-1) | Vs/
(m·s-1) | ρ/
(kg·m-3) | δN | δT | | 上层页岩 | 21.28 | 0.272 | 3268 | 1829 | 2500 | 0.248 | 0.090 | | 下层页岩 | 33.27 | 0.160 | 3678 | 2339 | 2620 | 0.056 | 0.024 |
|
The double-layer model 1 of gas-bearing shales
|

| E/GPa | σ | Vp/
(m·s-1) | Vs/
(m·s-1) | ρ/
(kg·m-3) | δN | δT | | 上层页岩 | 17.47 | 0.256 | 2960 | 1695 | 2420 | 0.181 | 0.068 | | 下层页岩 | 9.57 | 0.324 | 2430 | 1240 | 2350 | 0.104 | 0.032 |
|
The double-layer model 2 of gas-bearing shales
|
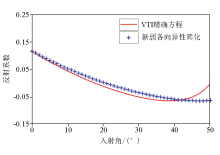
|
The accuracy analysis result of reflection coefficient equations based on double-layer gas-bearing shales model 1
|
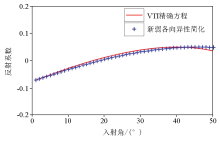
|
The accuracy analysis result of reflection coefficient equations based on double-layer gas-bearing shales model 2
|

| 流程 | 描述 | | 步骤1 | 初始化算法,设置马尔可夫链的数量及每条马尔可夫链的最大循环数 | | 步骤2 | 选择初始模型作为首次迭代的模型,并以此作为每条马尔可夫链的初始状态 | | 步骤3 | 在每条马尔可夫链中,由特定均值和方差的建议分布生成一个新的候选模型 | | 步骤4 | 根据所建立的后验概率目标函数,计算新的候选模型的接受概率 | | 步骤5 | 以一定概率接受新的候选模型 | | 步骤6 | 返回固定状态下的值作为单个马尔可夫链预测的结果,并以此计算每条马尔科夫链的候选模型及接受情况 | | 步骤7 | 取多此循环后稳定的多条马尔科夫链的平均值作为最终的反演结果 |
|
Solution flow of McMC algorithm nonlinear optimization
|
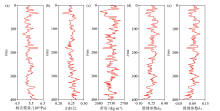
|
The rock physical models to be inverted
|
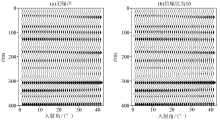
|
Forward synthetic seismogram
|

|
The inversion results at the synthesized seismogram of noise free
|
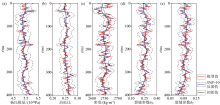
|
The inversion results at the synthesized seismogram with signal to noise ratio(SNR) equals 10
|
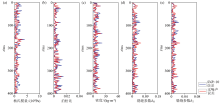
|
The absolute values of the error between the inversion results and the real models
|
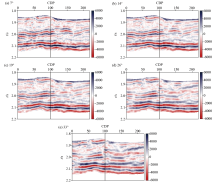
|
The actual pre-stack cross seismic data profiles
|
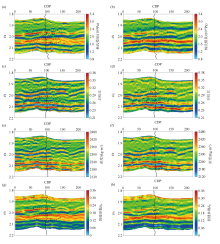
|
The nonlinear inversion results(left) and indirect fitting results from conventional linear inversion(right) elastic parameters of actual pre-stack seismic profiles
|
|
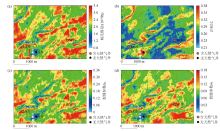
Interlayer slices of nonlinear actual pre-stack seismic inversion results of brittleness and fractural parameters
|
| [1] |
董大忠, 王玉满, 李新景, 等. 中国页岩气勘探开发新突破及发展前景思考[J]. 天然气工业, 2016, 36(1):19-32.
|
| [1] |
Dong D Z, Wang Y M, Li X J, et al. Breakthrough and prospect of shale gas exploration and development in China[J]. Natural Gas Industry, 2016, 36(1):19-32.
|
| [2] |
邹才能, 杨智, 崔景伟, 等. 页岩油形成机制、地质特征及发展对策[J]. 石油勘探与开发, 2013, 40(1):14-26.
|
| [2] |
Zou C N, Yang Z, Cui J W, et al. Formation mechanism,geological characteristics and development strategy of nonmarine shale oil in China[J]. Petroleum Exploration and Development, 2013, 40(1):14-26.
|
| [3] |
Zong Z Y, Yin X Y, Wu G C. Elastic impedance parameterization and inversion with Young's modulus and Poisson's ratio[J]. Geophysics, 2013, 78(6):N35-N42.
|
| [4] |
Grana D. Bayesian linearized rock-physics inversion[J]. Geophysics, 2016, 81(6):D625-D641.
|
| [5] |
de Figueiredo L P, Grana D, Bordignon F L, et al. Joint Bayesian inversion based on rock-physics prior modeling for the estimation of spatially correlated reservoir properties[J]. Geophysics, 2018, 83(5):M49-M61.
|
| [6] |
Chen H Z, Innanen K A, Chen T S. Estimating P- and S-wave inverse quality factors from observed seismic data using an attenuative elastic impedance[J]. Geophysics, 2018, 83(2):R173-R187.
|
| [7] |
Zhang F, Li X Y. Generalized approximations of reflection coefficients in orthorhombic media[J]. Journal of Geophysics and Engineering, 2013, 10(5):054004.
|
| [8] |
Sondergeld C H, Rai C S. Elastic anisotropy of shales[J]. The Leading Edge, 2011, 30(3):324-331.
|
| [9] |
张广智, 陈娇娇, 陈怀震, 等. 基于页岩岩石物理等效模型的地应力预测方法研究[J]. 地球物理学报, 2015, 58(6):2112-2122.
|
| [9] |
Zhang G Z, Chen J J, Chen H Z, et al. Prediction for in situ formation stress of shale based on rock physics equivalent model[J]. Chinese Journal of Geophysics, 2015, 58(6):2112-2122.
|
| [10] |
刘建伟, 张云银, 曾联波, 等. 非常规油藏地应力和应力甜点地球物理预测——渤南地区沙三下亚段页岩油藏勘探实例[J]. 石油地球物理勘探, 2016, 51(4):792-800,7.
|
| [10] |
Liu J W, Zhang Y Y, Zeng L B, et al. Geophysical prediction of stress and stress desserts in unconventional reservoirs:An example in Bonan area[J]. Oil Geophysical Prospecting, 2016, 51(4):792-800,7.
|
| [11] |
Plessix R E, Bork J. Quantitative estimate of VTI parameters from AVA responses[J]. Geophysical Prospecting, 2000, 48(1):87-108.
|
| [12] |
侯栋甲, 刘洋, 任志明, 等. 基于贝叶斯理论的VTI介质多波叠前联合反演[J]. 石油物探, 2014, 53(3):294-303.
|
| [12] |
Hou D J, Liu Y, Ren Z M, et al. Multi-wave prestack joint inversion in VTI media based on Bayesian theory[J]. Geophysical Prospecting for Petroleum, 2014, 53(3):294-303.
|
| [13] |
Lu J, Wang Y, Chen J Y, et al. Joint anisotropic amplitude variation with offset inversion of PP and PS seismic data[J]. Geophysics, 2018, 83(2):N31-N50.
|
| [14] |
Lang K, Yin X Y, Zong Z Y, et al. Anisotropic nonlinear inversion based on a novel PP wave reflection coefficient for VTI media[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023,61:5913613.
|
| [15] |
Bakulin A, Grechka V, Tsvankin I. Estimation of fracture parameters from reflection seismic data,Part II:Fractured models with orthorhombic symmetry[J]. Geophysics, 2000, 65(6):1803-1817.
|
| [16] |
Schoenberg M. Elastic wave behavior across linear slip interfaces[J]. The Journal of the Acoustical Society of America, 1980, 68(5):1516-1521.
|
| [17] |
Schoenberg M. Reflection of elastic waves from periodically stratified media with interfacial SLIP[J]. Geophysical Prospecting, 1983, 31(2):265-292.
|
| [18] |
Zoeppritz K, Erdbebnenwellen V. On the reflection and penetration of seismic waves through unstable layers[J]. Gottinger Nachrichten, 1919(1):66-84.
|
| [19] |
Rüger A. Reflection coefficients and azimuthal AVO analysis in anisotropic media[M]. Tulsa: Society of Exploration Geophysicists, 2002.
|
| [20] |
Graebner M. Plane-wave reflection and transmission coefficients for a transversely isotropic solid[J]. Geophysics, 1992, 57(11):1512.
|
| [1] |
HAN Lei, LI Jing-Ye, GENG Wei-Heng, WANG Yong-Ping, YANG Qi-Yu, ZHANG Yu-Ning. A method for calculating the P-to-S-wave velocity ratio through direct inversion of prestack multi-component seismic data based on the L1-2 norm constraint[J]. Geophysical and Geochemical Exploration, 2025, 49(3): 620-630. |
| [2] |
WANG Shu, WANG Rui, YANG Jia-Yi, ZHAO Wei-Sheng, LIAO Jian. High-resolution direct inversion of Poisson's impedance and fracture parameters using prestack seismic anisotropy data based on the non-stationary convolution model[J]. Geophysical and Geochemical Exploration, 2025, 49(3): 642-652. |
|
|
|
|
