基于Shearlet变换的三维地震数据重建

doi:10.11720/wtyht.2025.1271

Abstract
Figure/Table
References
Related Citation (3)

Download: PDF (6054 KB) HTML (1 KB)
Export: BibTeX | EndNote (RIS)

Abstract

Seismic data collected in the field frequently suffer from missing values due to constraints of acquisition cost or terrain. Data reconstruction is a critical step in seismic data preprocessing. Based on the compressed sensing theoretical framework, this study subsampled synthesized data using the 2D random undersampling technique. Then, the 3D seismic data were divided into a series of time slices. By introducing the sparse Shearlet transform and using the convex set projection (POCS) algorithm, this study conducted sequential data reconstruction for various time slices. As a result, a Shearlet transform-based time-domain 3D seismic data reconstruction method was developed. Numerical experiments and measured results demonstrate that the proposed reconstruction method exhibits a higher signal-to-noise ratio, a higher computational speed, and better effects than a Curvelet transform-based approach.

Key words： Shearlet transform seismic data reconstruction compression sensing convex set projection algorithm

Received: 26 June 2024 Published: 22 April 2025

ZTFLH:

P631.4

	Service

	E-mail this article
	Add to my bookshelf
	Add to citation manager
	E-mail Alert
	RSS
	Articles by authors
	Wei-Hong HUANG
	Hua ZHANG
	Zhao-Qi WU
	Meng-Xue DAI
	Xing-Yue BAO
	Wei-Long JIANG
	Xiu-Quan QIU

Cite this article:

Wei-Hong HUANG,Hua ZHANG,Zhao-Qi WU, et al. 3D seismic data reconstruction based on Shearlet transform[J]. Geophysical and Geochemical Exploration, 2025, 49(2): 394-403.

URL:

https://www.wutanyuhuatan.com/EN/10.11720/wtyht.2025.1271 OR https://www.wutanyuhuatan.com/EN/Y2025/V49/I2/394

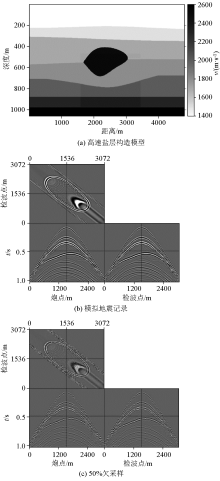
Synthesize data and corresponding speed model

Reconstructed SNR curves of the index and the new threshold model

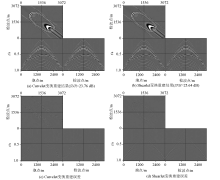
The reconstructed results and error by Curvelet and Shearlet

Reconstructed SNR curves by Curvelet and Shearlet

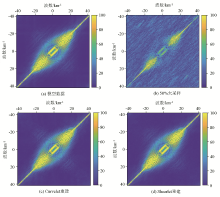
f-k spectrum of 2D random under-sampling reconstruction results

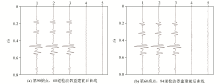
Single channel display of reconstruction results and errors
1—original record;2—Curvelet reconstruction results;3—Shearlet reconstruction results;4—Curvelet errors; 5—Shearlet errors

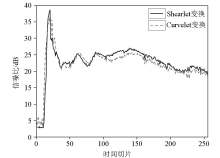
Reconstruction results of curved and shear wave bases and SNR of each time slice

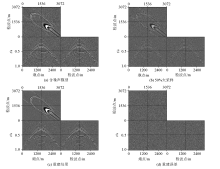
Reconstruction results of two-dimensional random under-sampling of noisy data and its error diagram

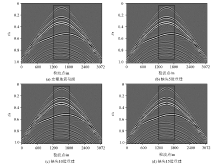
Continuous missing seismic trace reconstruction

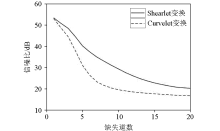
Continuous missing trace number and reconstructed SNR

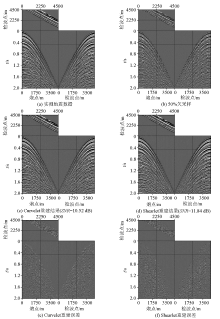
Reconstruction results of measured data

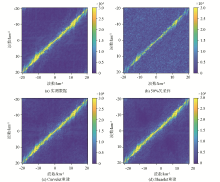
f-k spectrum of reconstructed measured data

[1]	霍志周, 熊登, 张剑锋. 地震数据重建方法综述[J]. 地球物理学进展, 2013, 28(4):1749-1756.
[1]	Huo Z Z, Xiong D, Zhang J F. The overview of seismic data reconstruction methods[J]. Progress in Geophysics, 2013, 28(4):1749-1756.
[2]	孟小红, 郭良辉, 张致付, 等. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建[J]. 地球物理学报, 2008, 51(1):235-241.
[2]	Meng X H, Guo L H, Zhang Z F, et al. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform[J]. Chinese Journal of Geophysics, 2008, 51(1):235-241.
[3]	Naghizadeh M, Sacchi M D. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J]. Geophysics, 2010, 75(6):WB189-WB202.
[4]	Gao J J, Sacchi M D, Chen X H. A fast reduced-rank interpolation method for prestack seismic volumes that depend on four spatial dimensions[J]. Geophysics, 2013, 78(1):V21-V30.
[5]	Ma J W. Three-dimensional irregular seismic data reconstruction via low-rank matrix completion[J]. Geophysics, 2013, 78(5):V181-V192.
[6]	蒋润, 李振春, 孙小东. 人工智能地震数据重建方法现状分析[J]. 地球物理学进展, 2023, 38(5):2047-2062.
[6]	Jiang R, Li Z C, Sun X D. Recent research status of seismic data reconstruction by artificial intelligence methods[J]. Progress in Geophysics, 2023, 38(5):2047-2062.
[7]	Yang P L, Gao J H, Chen W C. Curvelet-based POCS interpolation of nonuniformly sampled seismic records[J]. Journal of Applied Geophysics, 2012, 79:90-99.
[8]	Chen Y K, Chen X H, Wang Y F, et al. The interpolation of sparse geophysical data[J]. Surveys in Geophysics, 2019, 40(1):73-105.
[9]	Zwartjes P, Gisolf A. Fourier reconstruction with sparse inversion[J]. Geophysical Prospecting, 2007, 55(2):199-221.
[10]	郭刚明, 时立彩, 高生军, 等. 小波变换在地震资料处理中的应用效果分析[J]. 石油物探, 2003, 42(2):237-239,270.
[10]	Guo G M, Shi L C, Gao S J, et al. Application of wavelet transform in seismic data processing[J]. Geophysical Prospecting for Petrole, 2003, 42(2):237-239,270.
[11]	王本锋, 陈小宏, 李景叶, 等. POCS联合改进的Jitter采样理论曲波域地震数据重建[J]. 石油地球物理勘探, 2015, 50(1):20-28,13-14.
[11]	Wang B F, Chen X H, Li J Y, et al. Seismic data reconstruction based on POCS and improved Jittered sampling in the curvelet domain[J]. Oil Geophysical Prospecting, 2015, 50(1):20-28,13-14.
[12]	张华, 陈小宏. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 2013, 56(5):1637-1649.
[12]	Zhang H, Chen X H. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese Journal of Geophysics, 2013, 56(5):1637-1649.
[13]	Liu J C, Chou Y X, Zhu J J. Interpolating seismic data via the POCS method based on shearlet transform[J]. Journal of Geophysics and Engineering, 2018, 15(3):852-876.
[14]	Kong D H, Peng Z M. Seismic random noise attenuation using shearlet and total generalized variation[J]. Journal of Geophysics and Engineering, 2015, 12(6):1024-1035.
[15]	Guo K H, Kutyniok G, Labate D. Sparse multidimensional representations using anisotropic dilation and shear operators[J]. Wavelets and Splines, 2006:189-201.
[16]	Tekalp A M, Ozkan M K, Sezan M I. High-resolution image reconstruction from lower-resolution image sequences and space-varying image restoration[C]// [Proceedings] ICASSP-92:1992 IEEE International Conference on Acoustics,Speech,and Signal Processing. March 23-26,1992,San Francisco,CA,USA.IEEE, 1992:169-172.
[17]	Stark H, Oskoui P. High-resolution image recovery from image-plane arrays,using convex projections[J]. Journal of the Optical Society of America A,Optics and Image Science, 1989, 6(11):1715-1726.
[18]	Youla D C, Webb H. Image restoration by the method of convex projections:Part 1 theory[J]. IEEE Transactions on Medical Imaging, 1982, 1(2):81-94.
[19]	Ozkan M K, Tekalp A M, Sezan M I. POCS-based restoration of space-varying blurred images[J]. IEEE Transactions on Image Processing, 1994, 3(4):450-454.
[20]	Patti A J, Sezan M I, Murat Tekalp A. Superresolution video reconstruction with arbitrary sampling lattices and nonzero aperture time[J]. IEEE Transactions on Image Processing, 1997, 6(8):1064-1076.
[21]	Bregman L M. The method of successive projection for finding a common point of convex sets[J]. Dokl.akad.nauk Sssr, 1965, 6(3):487-490.
[22]	Gao J J, Chen X H, Li J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3):229-238.
[23]	Candès E, Demanet L, Donoho D, et al. Fast discrete curvelet transforms[J]. Multiscale Modeling & Simulation, 2006, 5(3):861-899.
[24]	Candes E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2):21-30.