|
|
|
| Bayesian prestack seismic stochastic inversion based on the exact Zoeppritz equation |
NIU Li-Ping1( ), HU Hua-Feng1, ZHOU Dan1, ZHENG Xiao-Dong2, GENG Jian-Hua3,4,5 ), HU Hua-Feng1, ZHOU Dan1, ZHENG Xiao-Dong2, GENG Jian-Hua3,4,5 |
1. SINOPEC Geophysical Research Institute Co.,Ltd.,Nanjing 211103,China
2. Research Institute of Petroleum Exploration and Development,PetroChina,Beijing 100083,China
3. State Key Laboratory of Marine Geology,Tongji University,Shanghai 200092,China
4. School of Ocean and Earth Science,Tongji University,Shanghai 200092,China
5. Research Center for Marine Resources,Tongji University,Shanghai 200092,China |
|
|
|
|
Abstract The prestack seismic inversion method based on the exact Zoeppritz equation is challenged by seismic data with low signal-to-noise ratios(SNRs).The Markov chain Monte Carlo(MCMC) simulation is a heuristic global optimization algorithm that can achieve effective prestack nonlinear inversion of elastic parameters.The conventional MCMC-based prestack inversion method,which characterizes the statistical properties of elastic parameters via the Gaussian distribution,has significant limitations when applied to complex lithologic reservoirs.Besides,due to the influence of the huge parameter space of subsurface models and the noise in seismic data,the MCMC search process for the posterior probability distribution of elastic parameters is very sensitive to local extrema,making it difficult to obtain stable and accurate results from MCMC-based prestack inversion.This study proposed an improved MCMC-based elastic parameter inversion method to address the challenges faced by the prestack inversion based on the exact Zoeppritz equation under the conditions of actual complex reservoirs and seismic data with low SNRs.First,the method reduced the complexity of the posterior probability distribution by transforming the parameters to be inverted into the perturbations of the model parameters using a low-frequency model (LFM) constraint.Then,the seismic forward modeling process was constrained by taking the logarithm of the likelihood function and utilizing an LFM.Finally,a multi-chain algorithm based on random subspace sampling was employed to perform global optimization for the prestack nonlinear inversion problems,thus avoiding premature convergence of the sampling process to local extrema.As indicated by the tests on the simulated data with low SNRs and the actual data,the method proposed in this study can yield more accurate and stable inversion results while providing credible and quantitative uncertainty estimates for the inversion results.
|
|
Received: 25 November 2022
Published: 26 February 2024
|
|
|
|
|
|
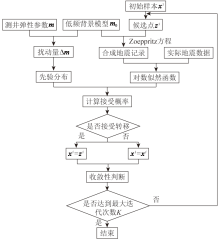
|
Flow chart of stochastic sampling for the elastic parameter perturbations
|

|
Real well logs of elastic parameters and the corresponding LFMs
|

|
Crossplots of the elastic parameters and the corresponding probability density contours obtained by fitting with Gaussian mixture distributions
|

|
Crossplots of elastic parameter perturbations and the corresponding probability density contours obtained by fitting with Gaussian distributions
|
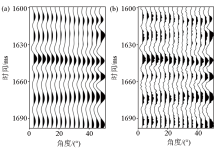
|
The synthetic seismic angle gathers
a—no noise;b—S/N is 3
|

|
The inversion results of the elastic parameters with noisy seismic data
|
R ^ with the number of iterations
">
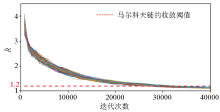
|
The variation of convergence diagnostic with the number of iterations
|

|
Statistical histogram of the sampling results for the elastic parameter perturbations at time 1630 ms
|

|
Statistical histogram of the sampling results for the elastic parameter perturbations at time 1672 ms
|
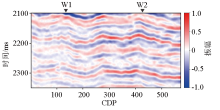
|
Poststack seismic section
|

|
Actual seismic angle gathers at different CDP
|

|
Low-frequency model
a—P-velocity;b—S-velocity;c—density
|

|
Crossplots of elastic parameter perturbations at well locations and the corresponding probability density contours obtained by fitting with Gaussian distributions
|
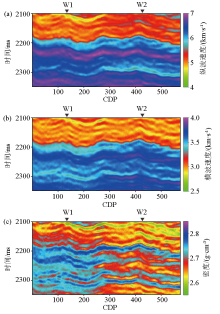
|
Inverted results of elastic parameters
a—P-velocity;b—S-velocity;c—density
|

|
Inverted results at well W1
a—P-velocity;b—S-velocity;c—density;d—the seismic angle gather at well
|

|
Inverted results at well W2
a—P-velocity;b—S-velocity;c—density;d—the seismic angle gather at well
|

|
Post standard deviation of elastic parameters
a—P-velocity;b—S-velocity and;c—density
|
R ^ with the number of iterations at different CDP
">

|
The variation of convergence diagnostic with the number of iterations at different CDP
|
| [1] |
Zoeppritz K. On the reflection and propagation of seismic waves[J]. Gottinger Nachrichten, 1919, 1(5):66-84.
|
| [2] |
Aki K, Richards P G. Quantitative seismology:Theory and methods[M]. San Francisco: W H Freeman,1980.
|
| [3] |
Shuey R T. A simplification of the Zoeppritz equations[J]. Geophysics, 1985, 50(4):609-614.

|
| [4] |
Wiggins R, Kenny G S, McClure C D. Common-depth method for determining and displaying the shear-velocity reflectivities of a geologic formation[J]. The Journal of the Acoustical Society of America, 1986, 79(2):589-590.
|
| [5] |
Mallick S. A simple approximation to the P-wave reflection coefficient and its implication in the inversion of amplitude variation with offset data[J]. Geophysics, 1993, 58(4):544-552.

|
| [6] |
Fatti J L, Smith G C, Vail P J, et al. Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9):1362-1376.

|
| [7] |
Goodway B, Chen T W, Downton J. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters;“λρ”,“μρ”,&“λ/μ fluid stack”,from P and S inversions[C]// SEG Technical Program Expanded Abstracts 1997,Society of Exploration Geophysicists, 1997:183-186.
|
| [8] |
Gray D, Goodway B, Chen T W. Bridging the gap:Using AVO to detect changes in fundamental elastic constants[C]// SEG Technical Program Expanded Abstracts 1999,Society of Exploration Geophysicists, 1999:852-855.
|
| [9] |
程彦, 董守华, 赵伟, 等. Zoeppritz方程近似解拟合精确解影响因素[J]. 物探与化探, 2010, 34(4):523-527.
|
| [9] |
Cheng Y, Dong S H, Zhao W, et al. The analysis of influencing factors between Zoeppritz approximate solution and exact solution[J]. Geophysical and Geochemical Exploration, 2010, 34(4):523-527.
|
| [10] |
Innanen K A, Mahmoudian F. Characterizing the degree of amplitude-variation-with-offset nonlinearity in seismic physical modelling reflection data[J]. Geophysical Prospecting, 2015, 63(1):133-140.

|
| [11] |
Vernik L. Seismic petrophysics in quantitative interpretation[M].Society of Exploration Geophysicists, 2016.
|
| [12] |
刘福平, 孟宪军, 王玉梅, 等. 反演纵横波速度的Jacobian矩阵及精确计算方法[J]. 中国科学:地球科学, 2010, 11(11):1608-1616.
|
| [12] |
Liu F P, Meng X J, Wang Y M, et al. Jacobian matrix for inversion of P- wave velocity and its accurate calculation method[J]. Scientia Sinica:Terrae, 2010, 40(11):1608-1616.

|
| [13] |
Zhi L X, Chen S Q, Li X Y. Joint AVO inversion of PP and PS waves using exact Zoeppritz equation[C]// SEG Technical Program Expanded Abstracts 2013,Society of Exploration Geophysicists,2013.
|
| [14] |
Zong Z Y, Yin X Y, Wu G C. Multi-parameter nonlinear inversion with exact reflection coefficient equation[J]. Journal of Applied Geophysics, 2013, 98:21-32.

|
| [15] |
Zhi L X, Chen S Q, Li X Y. Amplitude variation with angle inversion using the exact Zoeppritz equations:Theory and methodology[J]. Geophysics, 2016, 81(2):N1-N15.

|
| [16] |
Yin X Y, Cheng G S, Zong Z Y. Non-linear AVO inversion based on a novel exact PP reflection coefficient[J]. Journal of Applied Geophysics, 2018, 159:408-417.

|
| [17] |
张凌远, 张宏兵, 尚作萍, 等. 基于Zoeppritz方程的叠前和叠后混合多参数非线性地震反演[J]. 石油地球物理勘探, 2021, 56(1):164-171.
|
| [17] |
Zhang L Y, Zhang H B, Shang Z P, et al. Nonlinear multi-parameter hybrid inversion of prestack and post-stack seismic data based on Zoeppritz equation[J]. Oil Geophysical Prospecting, 2021, 56(1):164-171,11.
|
| [18] |
Mallick S, Adhikari S. Amplitude-variation-with-offset and prestack-waveform inversion:A direct comparison using a real data example from the Rock Springs Uplift,Wyoming,USA[J]. Geophysics, 2015, 80(2):B45-B59.

|
| [19] |
冉然, 宋建国. 基于Zoeppritz方程的纵横波模量反演[J]. 物探与化探, 2017, 41(4):707-714.
|
| [19] |
Ran R, Song J G. Compressional and shear modulus inversion based on Zoeppritz equation[J]. Geophysical and Geochemical Exploration, 2017, 41(4):707-714.
|
| [20] |
Gholami A, Aghamiry H S, Abbasi M. Constrained nonlinear amplitude variation with offset inversion using Zoeppritz equations[J]. Geophysics, 2018, 83(3):R245-R255.

|
| [21] |
Riedel M, Dosso S E, Beran L. Uncertainty estimation for amplitude variation with offset(AVO) inversion[J]. Geophysics, 2003, 68(5):1485-1496.

|
| [22] |
White J. Computer model inversion and uncertainty quantification in the geosciences[D]. Tampa: University of South Florida, 2014.
|
| [23] |
张广智, 王丹阳, 印兴耀, 等. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报, 2011, 54(11):2926-2932.
|
| [23] |
Zhang G Z, Wang D Y, Yin X Y, et al. Study on prestack seismic inversion using Markov chain Monte Carlo[J]. Chinese Journal of Geophysics, 2011, 54(11):2926-2932.
|
| [24] |
印兴耀, 孔栓栓, 张繁昌, 等. 基于差分进化算法的叠前AVO反演[J]. 石油地球物理勘探, 2013, 48(4):591-596,676,503.
|
| [24] |
Yin X Y, Kong S S, Zhang F C, et al. Prestack AVO inversion based on the differential evolution algorithm[J]. Oil Geophysical Prospecting, 2013, 48(4):591-596,676,503.
|
| [25] |
Grana D, Fjeldstad T, Omre H. Bayesian Gaussian mixture linear inversion for geophysical inverse problems[J]. Mathematical Geosciences, 2017, 49(4):493-515.

|
| [26] |
de Figueiredo L P, Grana D, Roisenberg M, et al. Gaussian mixture Markov chain Monte Carlo method for linear seismic inversion[J]. Geophysics, 2019, 84(3):R463-R476.
|
| [27] |
Aleardi M, Salusti A. Markov chain Monte Carlo algorithms for target-oriented and interval-oriented amplitude versus angle inversions with non-parametric priors and non-linear forward modellings[J]. Geophysical Prospecting, 2020, 68(3):735-760.
|
| [28] |
Pan X P, Zhang G Z, Zhang J J, et al. Zoeppritz-based AVO inversion using an improved Markov chain Monte Carlo method[J]. Petroleum Science, 2017, 14(1):75-83.

|
| [29] |
Vrugt J A. Markov chain Monte Carlo simulation using the DREAM software package:Theory,concepts,and MATLAB implementation[J]. Environmental Modelling & Software, 2016, 75:273-316.
|
| [30] |
Tarantola A. Inverse problem theory[M]. Elsevier Science,1987.
|
| [31] |
Niu L P, Ma J Q, Geng J H, et al. Mixture density network applied to reservoir parameter inversion in Bohai Oil field[C]// New Orleans: SEG Technical Program Expanded Abstracts 2015,Society of Exploration Geophysicists, 2015:2806-2810.
|
| [32] |
Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equation of State Calculations by Fast Computing Machines[J]. The Journal of Chemical Physics, 1953, 21(6):1087-1092.

|
| [33] |
Gelman A, Rubin D B. Inference from iterative simulation using multiple sequences[J]. Statistical Science, 1992, 7(4):457-472.
|
|
|
|

