|
|
|
| Methods for wavenumber-domain transform calculation and DEXP-based quantitative interpretation of third-order gradient tensor anomalies of gravitational potential |
QIU Feng( ) ) |
| Research Institute of Building Materials and Geomechanics, Jiangxi Academy of Water Science and Engineering, Nanchang 330029, China |
|
|
|
|
Abstract Since the current instrumental measurement technology cannot directly measure the third-order gradient tensor of gravitational potential, this study proposed a wavenumber-domain transform calculation method for the third-order gradient tensor of gravitational potential based on the gravity anomaly and gradient tensor data. To verify the correctness of this method, this study computed the third-order gradient tensor anomalies of gravitational potential using a 3D model and compared the wavenumber-domain transform calculation results with the forward modeling results, suggesting that the wavenumber-domain transform calculation method is feasible. Moreover, the wavenumber-domain transform calculation results based on gravitational gradient tensor data were more accurate than those based on gravity anomaly data, yielding a root mean square error not exceeding 1 pMKS. In addition, based on the measured data of the Vinton salt dome area, the third-order gradient tensor data of gravitational potential of this area were obtained using the wavenumber-domain transform calculation method. The obtained data were used for DEXP-based data interpretation, attaining consistent depth and boundary results with the previous research results.
|
|
Received: 01 October 2022
Published: 23 January 2024
|
|
|
|
|
|
|
Geometric schematic diagram of upright cuboid model
|
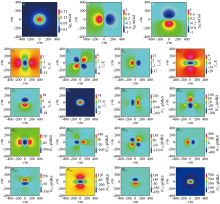
|
The gravity tensor anomalies from first-order to third-order of upright cuboid model
|

|
The deviations between the FFT-derived and model-calculated third-order gradient tensor of gravitational potential from gravity value
|

| 模型的RMS误差/pMKS | 重力位三阶梯度张量 | | Wxxx | Wxxy | Wxxz | | Wxyz | Wxzz | Wyyy | Wyyz | Wyzz | Wzzz | | 不去除边界畸变值 | 7.66 | 0.17 | 10.61 | 0.16 | 0.04 | 7.64 | 7.32 | 10.11 | 7.29 | 14.66 | | 去掉部分边界畸变值 | 2.54 | 0.17 | 0.17 | 0.16 | 0.04 | 2.51 | 2.43 | 0.16 | 2.39 | 0.23 |
|
RMS error between model and FFT third-order gradient tensor of gravitational potential
|

|
The deviations between the FFT-derived and model-calculated third-order gradient tensor of gravitational potential from gravity gradient tensor
|

| 重力位三阶梯度张量 | Wxxx | Wxxy | Wxxz | Wxyy | Wxyz | Wxzz | Wyyy | Wyyz | Wyzz | Wzzz | | 模型的RMS误差/pMKS | 0.15 | 0.14 | 0.47 | 0.14 | 0.04 | 0.06 | 0.15 | 0.47 | 0.06 | 0.90 |
|
RMS error between model and FFT third-order gradient tensor of gravitational potential
|
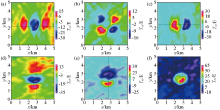
|
Gravity gradient tensor data in Vinton salt dome area after processing
|

|
The third-order gradient tensor data of the gravity level in the Vinton salt dome area obtained by conversion
|

|
DEXP transformation result of the third-order tensor data of gravity potential obtained by wavenumber domain transformation
|
| [1] |
Balakin A B, Daishev R A, Murzakhanov Z G, et al. Laser-interferometric detector of the first,second and third derivatives of the potential of the Earth gravitational field[J]. Izvestiya vysshikh uchebnykh zavedenii,seriya Geologiya i Razvedka, 1997, 1:101-107.
|
| [2] |
DiFrancesco D, Meyer T J, Christensen A, et al. Gravity gradiometry-today and tomorrow[C]// 11th SAGA Biennial Technical Meeting and Exhibition, 2009.
|
| [3] |
Brieden P, Muller J, Flury J, et al. The mission OPTIMA-novelties and benefit[R]. Geotechnologien,Science Report, 2010.
|
| [4] |
Fantino E, Casotto S. Methods of harmonic synthesis for global geopotential models and their first-,second- and third-order gradients[J]. Journal of Geodesy, 2009, 83(7):595-619.

|
| [5] |
Casotto S, Fantino E. Gravitational gradients by tensor analysis with application to spherical coordinates[J]. Journal of Geodesy, 2009, 83(7):621-634.

|
| [6] |
Fukushima T. Numerical computation of spherical harmonics of arbitrary degree and order by extending exponent of floating point numbers:II first-,second-,and third-order derivatives[J]. Journal of Geodesy, 2012, 86(4):271-285.

|
| [7] |
Rosi G, Cacciapuoti L, Sorrentino F, et al. Measurements of the gravity-field curvature by atom interferometry[J]. Physical Review Letters, 2015, 114(1):13001.
|
| [8] |
Rothleitner C, Francis O. Measuring the Newtonian constant of gravitation with a differential free-fall gradiometer:A feasibility study[J]. The Review of Scientific Instruments, 2014, 85(4):469-526.
|
| [9] |
陈钊, 李辉, 邢乐林, 等. 重力垂直梯度非线性变化研究[J]. 大地测量与地球动力学, 2014, 34(2):27-30.
|
| [9] |
Chen Z, Li H, Xing L L, et al. Study on non-linear variation of vertical gradient of gravity[J]. Journal of Geodesy and Geodynamics, 2014, 34(2):27-30.
|
| [10] |
Fedi M. DEXP:A fast method to determine the depth and the structural index of potential fields sources[J]. Geophysics, 2007, 72(1):I1-I11.
|
| [11] |
Fedi M, Abbas M A. A fast interpretation of self-potential data using the depth from extreme points method[J]. Geophysics, 2013, 78(2):E107-E116.
|
| [12] |
杜劲松, 邱峰. 重力位三阶梯度张量及其勘探能力初步分析[J]. 大地测量与地球动力学, 2019, 39(4):331-338.
|
| [12] |
Du J S, Qiu F. Third-order gradient tensor of gravitational potential and its exploration capacity analysis[J]. Geodesy and Geodynamics, 2019, 39(4):331-338.
|
| [13] |
邱峰, 杜劲松, 陈超. 重力异常及其梯度张量DEXP定量解释方法的影响因素分析[J]. 物探与化探, 2020, 44(3):540-549.
|
| [13] |
Qiu F, Du J S, Chen C. Influence factor analysis of quantitative interpretation for gravity anomaly and its gradient tensor by DEXP[J]. Geophysical and Geochemical Exploration, 2020, 44(3):540-549.
|
| [14] |
Mickus K L, Hinojosa J H. The complete gravity gradient tensor derived from the vertical component of gravity:a Fourier transform technique[J]. Journal of Applied Geophysics, 2001, 46(3):159-174.

|
| [15] |
舒晴, 朱晓颖, 周坚鑫, 等. 重力梯度张量分量频率域转换处理方法[J]. 地球物理学进展, 2016. 31(6):2633-2640.
|
| [15] |
Shu Q, Zhu X Y, Zhou J X, et al. Frequency domain transformation method for gravity gradient tensor components[J]. Progress in Geophysics, 2016, 31(6):2633-2640.
|
| [16] |
邱峰, 杜劲松, 陈超. 矩形棱柱体重力位三阶梯度张量正演计算公式[J]. 大地测量与地球动力学, 2019, 39(3):313-316.
|
| [16] |
Qiu F, Du J S, Chen C. Forward modeling formulae for third-order gradient tensor of gravitational potential caused by the right rectangular prism[J]. Journal of Geodesy and Geodynamics, 2019, 39(3):313-316.
|
| [17] |
Li X. Vertical resolution:Gravity versus vertical gravity gradient[J]. The Leading Edge, 2001, 20(8):901-904.

|
| [18] |
Oliveira V C, Barbosa V C F. 3D radial gravity gradient inversion[J]. Geophysical Journal International, 2013, 195(2):883-902.

|
| [19] |
Geng M X, Huang D N, Yang Q J, et al. 3D inversion of airborne gravity-gradiometry data using cokriging[J]. Geophysics, 2014, 79(4):G37-G47.
|
| [20] |
Ennen C. Mapping gas-charged fault blocks around the Vinton Salt Dome,Louisiana using gradiometry data[D]. Houston: University of Houston, 2012.
|
|
|
|

