基于OMAGA-BP算法的高密度电阻率法反演研究

doi:10.11720/wtyht.2023.1560

Abstract
Figure/Table
References
Related Citation (10)

Download: PDF (2754 KB) HTML (1 KB)
Export: BibTeX | EndNote (RIS)

Abstract

High-density resistivity method is widely used in engineering exploration because of its efficient and intuitive features. However, due to the high nonlinearity of the inversion problem, the traditional inversion method has some inaccuracy in describing the boundary of anomalous body. In order to achieve high precision two-dimensional nonlinear inversion imaging with high-density electrical method, to overcome the problem that a large number of saddle points in the parameter space of loss function of BP algorithm affect the calculation accuracy and that it is difficult to assign optimal weight threshold to BP network due to the precocious convergence of general genetic algorithm. In this paper,an Optimum Maintaining Adaptive Genetic Algorithm(OMAGA)is proposed to optimize the BP neural network for high density electrical two-dimensional inversion imaging. Good results have been obtained for the inversion calculation of simulation model data and measured data through this method, it shows that this method has strong generalization ability and high inversion accuracy. This study is helpful for the accurate inversion of high density resistivity method in the future,it is helpful to improve the accuracy of underground target identification.

Key words： optimum maintaining adaptive genetic algorithm BP nerual network high-density electrical method inversion accuracy

Received: 22 November 2022 Published: 23 January 2024

P631

	Service

	E-mail this article
	Add to my bookshelf
	Add to citation manager
	E-mail Alert
	RSS
	Articles by authors
	Xiang-Hao LIU
	Si-Xin LIU
	Ming-Qi HU
	Zhong-Qiu SUN
	Qian WANG

Cite this article:

Xiang-Hao LIU,Si-Xin LIU,Ming-Qi HU, et al. Research on inversion of high-density resistivity method based on OMAGA-BP algorithm[J]. Geophysical and Geochemical Exploration, 2023, 47(6): 1519-1527.

URL:

https://www.wutanyuhuatan.com/EN/10.11720/wtyht.2023.1560 OR https://www.wutanyuhuatan.com/EN/Y2023/V47/I6/1519

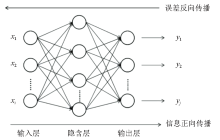
Schematic diagram of three-layer BP neural network structure

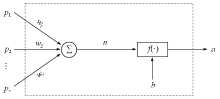
Schematic diagram of single neuron formula

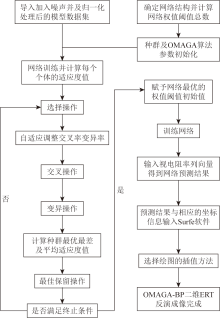
2D OMAGA-BP high-density electrical inversion imaging diagram

Schematic diagram of some resistivity model samples

Performance comparison of three networks trained with simulated data

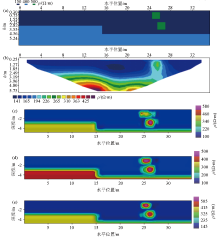
Schematic diagram of the test model and inversion imaging results of different methods
a—schematic diagram of the test resistivity model;b—least-squares inversion result of resistivity model;c—BP inversion result;d—GA-BP inversion result;e—OMAGA-BP inversion result

Bomb shelter and its data acquisition diagram

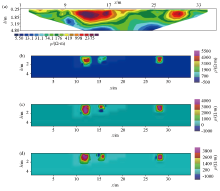
Inversion results of air raid shelter data by four inversion methods
a—least-squares inversion result;b—BP inversion result;c—GA-BP inversion result; d—OMAGA-BP inversion result

[1]	杨文采. 地球物理反演的理论与方法[M]. 北京: 地质出版社,1997.
[1]	Yang W C. Theory and method of geophysical inversion[M]. Beijing: The Geological Publishing House,1997.
[2]	何继善. 电法勘探的发展和展望[J]. 地球物理学报, 1997, 40(S1):308-316.
[2]	He J S. Development and prospect of electrical prospecting method[J]. Chinese Journal of Geophysics, 1997, 40(S1):308-316.
[3]	何门贵, 温永辉. 高密度电阻率法二维反演在工程勘探中的应用[J]. 物探与化探, 2002, 26(2):156-159.
[3]	He M G, Wen Y H. The application of high density resistivity 2D inversion to engineering exploration[J]. Geophysical and Geochemical Exploration, 2002, 26(2):156-159.
[4]	吕惠进, 刘少华, 刘伯根. 高密度电阻率法在地面塌陷调查中的应用[J]. 地球物理学进展, 2005, 20(2):381-386.
[4]	Lyu H J, Liu S H, Liu B G. Application of resistivity tomography survey method in detecting ground subsidence[J]. Progress in Geophysics, 2005, 20(2):381-386.
[5]	Loke M H, Barker R D. Least-squares deconvolution of apparent resistivity pseudosections[J]. Geophysics, 1995, 60(6):1682-1690.
[6]	徐海浪, 吴小平. 电阻率二维神经网络反演[J]. 地球物理学报, 2006, 49(2):584-589.
[6]	Xu H L, Wu X P. 2-D resistivity inversion using the neural network method[J]. Chinese Journal of Geophysics, 2006, 49(2):584-589.
[7]	Raiche A. A pattern recognition approach to geophysical inversion using neural nets[J]. Geophysical Journal International, 1991, 105(3):629-648.
[8]	Calderón-Macías C, Sen M K, Stoffa P L. Artificial neural networks for parameter estimation in geophysics[J]. Geophysical Prospecting, 2000, 48(1):21-47.
[9]	El-Qady G, Ushijima K. Inversion of DC resistivity data using neural networks[J]. Geophysical Prospecting, 2001, 49(4):417-430.
[10]	Stephen J, Manoj C, Singh S B. A direct inversion scheme for deep resistivity sounding data using artificial neural networks[J]. Journal of Earth System Science, 2004, 113(1):49-66.
[11]	Mann C J H. Geophysical applications of artificial neural networks and fuzzy logic[J]. Kybernetes, 2006, 35(3/4):599-600.
[12]	Neyamadpour A, Taib S, Wan-Abdullah W A T W. Using artificial neural networks to invert 2D DC resistivity imaging data for high resistivity contrast regions: A MATLAB application[J]. Computers & Geosciences, 2009, 35(11):2268-2274.
[13]	Neyamadpour A, Wan-Abdullah W A T, Taib S. Inversion of quasi-3D DC resistivity imaging data using artificial neural networks[J]. Journal of Earth System Science, 2010, 119(1): 27-40.
[14]	Neyamadpour A, Wan-Abdullah W A T, Taib S, et al. 3D inversion of DC data using artificial neural networks[J]. Studia Geophysica et Geodaetica, 2010, 54(3):465-485.
[15]	Maiti S, Gupta G, Erram V C,et.al. Inversion of Schlumberger resistivity sounding data from the critically dynamic Koyna region using the Hybrid Monte Carlo-based neural network approach[J]. Nonlinear Processes in Geophysics, 2011, 18(2):179-192.
[16]	张凌云. 高密度电阻率勘探反演的非线性方法研究[D]. 太原: 太原理工大学, 2011.
[16]	Zhang L Y. The study of nonlinear inversion method in high-density resistivity method inversion[D]. Taiyuan: Taiyuan University of Technology, 2011.
[17]	戴前伟, 江沸菠. 基于混沌振荡PSO-BP算法的电阻率层析成像非线性反演[J]. 中国有色金属学报, 2013, 23(10):2897-2904.
[17]	Dai Q W, Jiang F B. Nonlinear inversion for electrical resistivity tomography based on chaotic oscillation PSO-BP algorithm[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(10):2897-2904.
[18]	Dai Q W, Jiang F B, Dong L. Nonlinear inversion for electrical resistivity tomography based on chaotic DE-BP algorithm[J]. Journal of Central South University, 2014, 21(5):2018-2025.
[19]	高明亮, 于生宝, 郑建波, 等. 基于IGA算法的电阻率神经网络反演成像研究[J]. 地球物理学报, 2016, 59(11):4372-4382.
[19]	Gao M L, Yu S B, Zheng J B, et al. Research of resistivity imaging using neural network based on immune genetic algorithm[J]. Chinese Journal of Geophysics, 2016, 59(11):4372-4382.
[20]	Wu X X, Liu J G. A new early stopping algorithm for improving neural network generalization[C]// 2009 Second International Conference on Intelligent Computation Technology and Automation.Changsha,China,IEEE, 2009:15-18.
[21]	Dauphin Y N, Pascanu R, Gulcehre C, et al. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization[C]// Proceedings of the 27^th International Conference on Neural Information Processing Systems, 2014.
[22]	恽为民, 席裕庚. 遗传算法的全局收敛性和计算效率分析[J]. 控制理论与应用, 1996, 13(4): 455-460.
[22]	Hun W M, Xi Y G. The analysis of global convergence and computational efficiency for genetic algorithm[J]. Control Theory & Applications, 1996, 13(4):455-460.
[23]	Chen L, Gallet A, Huang S S, et al. Probabilistic cracking prediction via deep learned electrical tomography[J]. Structural Health Monitoring, 2022, 21(4): 1574-1589.
[24]	Bishop C M. Training with noise is equivalent to tikhonov regularization[J]. Neural Computation, 1995, 7(1):108-116.
[25]	An Z. The effects of adding noise during backpropagation training on a generalization performance[J]. Neural Computation, 1996, 8(3):643-674.