|
|
|
| A 1D inversion system of the ground-based loop-source transient electromagnetic method |
ZHANG Wen-Bo( ), ZHANG Ying, LI Jian-Hui( ), ZHANG Ying, LI Jian-Hui( ) ) |
| Institute of Geophysics and Geomatics, China University of Geosciences (Wuhan), Wuhan 430074, China |
|
|
|
|
Abstract The processing and interpretation of the data derived using the transient electromagnetic (TEM) method are still mainly conducted through one-dimensional (1D) inversion presently. Therefore, developing an efficient and stable 1D inversion system with complete functions is greatly significant for further promoting the applications of the ground-based loop-source TEM method in China. This study developed such an inversion system, which involves four methods, namely minimum-structure inversion, Occam's inversion, laterally constrained inversion (LCI), and spatially constrained inversion (SCI). The first two methods are based on the Gauss-Newton method, and the others are based on the damped least-square method. This 1D inversion system was applied to detect the occurrence forms of the basalt rock masses in the Narenbaolige coalfield in Inner Mongolia. Then, the results derived from the minimum-structure inversion and Occam's inversion used in the 1D inversion system were compared with those obtained using the commercial software IX1D. As shown in the 2D pseudosection maps of resistivity obtained by these inversion methods, the basalt rock masses have similar occurrence forms and consistent resistivity range. Compared with drilling data, these 1D inversion results clearly reflected the distribution patterns of basalt rock masses in the Narenbaolige coalfield except for the upwelling channels of magmas. Afterward, the LCI and SCI were also applied to the coalfield. The results indicate a decrease in the resistivity differences of the basalt rock masses between adjacent survey points and an increase in the continuity of the interfaces between the basalts and sedimentary rocks.
|
|
Received: 24 December 2021
Published: 03 January 2023
|
|
|
|
Corresponding Authors:
LI Jian-Hui
E-mail: zhwb_000@126.com;ljhiiicumt@126.com
|
|
|
|
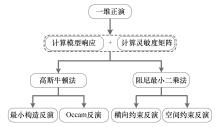
|
The framework of the 1D inversion system
|
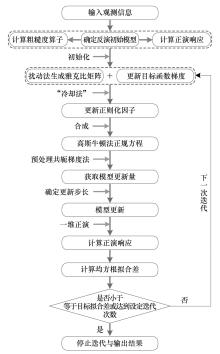
|
The flow chart for the 1D minimum-structure inversion
|
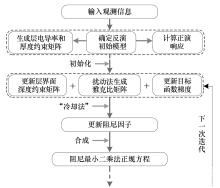
|
The flow chart for the 1D LCI and SCI
|
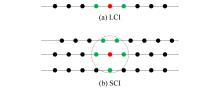
|
The diagram showing the observation points used as constrained points in the LCI and SCI
|

|
The distribution diagram of measuring points in the Narenbaolige coalfield
|
|
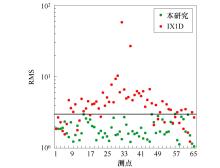
The comparison of RMS for IX1D software and the minimum-structure inversion method presented here
|

|
The section view stitched from the single-point 1D inversion models for survey line 160
|

|
The plane view of the 1D minimum-structure inversion results (z=0 m)
|

|
The section view stitched from LCI inversion models for survey line 160
|

|
The plane view of the LCI results (z=0 m, α=β=1 000)
|

|
The section view stitched from SCI inversion models for survey line 160
|

|
The plane view of the SCI results (z=0 m, α=β=10)
|

|
The plane view of the SCI results (z=0 m,α=β=100)
|

|
The plane view of the SCI results (z=0 m, α=β=1 000)
|
| [1] |
Auken E, Christiansen A V, Kirkegaard C, et al. An overview of a highly versatile forward and stable inverse algorithm for airborne, ground-based and borehole electromagnetic and electric data[J]. Exploration Geophysics, 2015, 46(3): 223-235.

|
| [2] |
殷长春, 刘云鹤, 熊彬. 地球物理三维电磁反演方法研究动态[J]. 中国科学:地球科学, 2020, 50(3):432-435.
|
| [2] |
Yin C C, Liu Y H, Xiong B. Status and prospect of 3D inversions in EM geophysics[J]. Science China Earth Sciences, 2020, 50(3): 432-435.
|
| [3] |
Smith J T, Booker J R. Magnetotelluric inversion for minimum structure[J]. Geophysics, 1988, 53(12): 1565-1576.

|
| [4] |
李帝铨, 王光杰, 底青云, 等. 基于遗传算法的CSAMT最小构造反演[J]. 地球物理学报, 2008, 51(4):1234-1245.
|
| [4] |
Li D Q, Wang G J, Di Q Y, et al. The application of genetic algorithm to CSAMT inversion for minimum structure[J]. Chinese Journal of Geophysics, 2008, 51(4): 1234-1245.
|
| [5] |
Constable S C, Parker R L, Constable C G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300.

|
| [6] |
Auken E, Christiansen A V. Layered and laterally constrained 2D inversion of resistivity data[J]. Geophysics, 2004, 69(3): 752-761.

|
| [7] |
Viezzoli V, Christiansen A V, Auken E, et al. Quasi-3D modeling of airborne TEM data by spatially constrained inversion[J]. Geophysics, 2008, 73(3): 105-113.
|
| [8] |
Farquharson C G, Oldenburg D W. Inversion of time-domain electromagnetic data for a horizontally layered earth[J]. Geophysical Journal International, 1993, 114(3): 433-442.

|
| [9] |
Farquharson C G, Oldenburg D W, Li Y G. An approximate inversion algorithm for time-domain electromagnetic surveys[J]. Journal of Applied Geophysics, 1999, 42(2): 71-80.

|
| [10] |
Yang D K, Oldenburg D W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit[J]. Geophysics, 2012, 77(2): B23-B34.

|
| [11] |
Scholl C, Helwig S L, Tezkan B, et al. 1-D multimodel joint inversion of TEM-data over multidimensional structures[J]. Geophysical Journal International, 2009, 176(1): 81-94.

|
| [12] |
Sudha, Tezkan B, Siemon B. Appraisal of a new 1D weighted joint inversion of ground based and helicopter-borne electromagnetic data[J]. Geophysical Prospecting, 2014, 62(3): 597-614.

|
| [13] |
Haroon A, Adrian J, Bergers R, et al. Joint inversion of long-offset and central-loop transient electromagnetic data: Application to a mud volcano exploration in Perekishkul, Azerbaijan[J]. Geophysical Prospecting, 2015, 63(2): 478-494.

|
| [14] |
Yogeshwar P, Küpper M, Tezkan B, et al. Innovative boat-towed transient electromagnetics—Investigation of the Furnas volcanic lake hydrothermal system, Azores[J]. Geophysics, 2020, 85(2): E41-E56.

|
| [15] |
Auken E, Christiansen A V, Jacobsen L H, et al. A resolution study of buried valleys using laterally constrained inversion of TEM data[J]. Journal of Applied Geophysics, 2008, 65(1): 10-20.

|
| [16] |
Kirkegaard C, Auken E. A parallel, scalable and memory efficient inversion code for very large-scale airborne electromagnetics surveys[J]. Geophysical Prospecting, 2015, 63(2): 495-507.

|
| [17] |
殷长春, 邱长凯, 刘云鹤, 等. 时间域航空电磁数据加权横向约束反演[J]. 吉林大学学报:地球科学版, 2016, 46(1):254-261.
|
| [17] |
Yin C C, Qiu C K, Liu Y H, et al. Weighted laterally-constrained inversion of time-domain airborne electromagnetic data[J]. Journal of Jilin University:Earth Science Edition, 2016, 46(1): 254-261.
|
| [18] |
殷长春, 朱姣, 邱长凯, 等. 航空电磁拟三维模型空间约束反演[J]. 地球物理学报, 2018, 61(6):2537-2547.
|
| [18] |
Yin C C, Zhu J, Qiu C K, et al. Spatially constrained inversion for airborne EM data using quasi-3D models[J]. Chinese Journal of Geophysics, 2018, 61(6): 2537-2547.
|
| [19] |
齐彦福, 殷长春, 王若, 等. 多通道瞬变电磁m序列全时正演模拟与反演[J]. 地球物理学报, 2015, 58(7):2566-2577.
|
| [19] |
Qi Y F, Yin C C, Wang R, et al. Multi-transient EM full-time forward modeling and inversion of m-sequences[J]. Chinese Journal of Geophysics, 2015, 58(7): 2566-2577.
|
| [20] |
Li J F, Liu Y H, Yin C C, et al. Fast imaging of time-domain airborne EM data using deep learning technology[J]. Geophysics, 2020, 85(5): E163-E170.

|
| [21] |
Li Z H, Huang Q H, Xie X B, et al. A generic 1D forward modeling and inversion algorithm for TEM sounding with an arbitrary horizontal loop[J]. Pure and Applied Geophysics, 2016, 173(8): 2869-2883.

|
| [22] |
Li M X, Cheng J L, Wang P, et al. Transient electromagnetic inversion based on the PSO-DLS combination algorithm[J]. Exploration Geophysics, 2019, 50(5): 472-480.

|
| [23] |
孙怀凤, 张诺亚, 柳尚斌, 等. 基于L1范数的瞬变电磁非线性反演[J]. 地球物理学报, 2019, 62(12):4860-4873.
|
| [23] |
Sun H F, Zhang N Y, Liu S B, et al. L1-norm based nonlinear inversion of transient electromagnetic data[J]. Chinese Journal of Geophysics, 2019, 62(12): 4860-4873.
|
| [24] |
Key K. 1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers[J]. Geophysics, 2009, 74(2): 9-20.
|
| [25] |
Anderson W L. Fourier cosine and sine transforms using lagged convolutions in double-precision (subprograms DLAGF0/DLAGF1)[R]. U.S. Geological Survey, 1983:83-320.
|
| [26] |
李建慧, 朱自强, 刘树才, 等. 基于Gaver-Stehfest算法的矩形发射回线激发的瞬变电磁场[J]. 石油地球物理勘探, 2011, 46(3):489-492.
|
| [26] |
Li J H, Zhu Z Q, Liu S C, et al. Rectangular loop transient electromagnetic field expressed by Gaver-Stehfest algorithm[J]. Oil Geophysical Prospecting, 2011, 46(3): 489-492.
|
| [27] |
Li J H, Farquharson C G, Hu X Y. Three effective inverse Laplace transform algorithms for computing time-domain electromagnetic responses[J]. Geophysics, 2016, 81(2): E113-E128.

|
| [28] |
Aster R C, Borchers B, Thurber C H. Parameter Estimation and Inverse Problems[M]. Amsterdam: Elsevier Academic Press, 2005.
|
| [29] |
Haber E. Computational methods in geophysical electromagnetics[M]. Philadelphia: SIAM. 2015.
|
| [30] |
李建慧. 基于矢量有限单元法的大回线源瞬变电磁法三维数值模拟[D]. 长沙: 中南大学, 2011.
|
| [30] |
Li J H. 3D numerical simulation for transient electromagnetic field excited by large Source loop based on vector finite element method[D]. Changsha: Central South University, 2011.
|
| [1] |
YOU Xi-Ran, ZHANG Ji-Feng, SHI Yu. Artificial neural network-based transient electromagnetic imaging[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1206-1214. |
| [2] |
QUE Ze-Sheng, LI Guan-Chao, HU Ying, JIAN Rui-Min, LIU Bing. GIS-based assessment of the radioactivity levels and risks of soil environment[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1336-1347. |
|
|
|
|

