|
|
|
| Random noise attenuation of common offset gathers by f-x low-rank matrix approximation with nonconvex regularization |
SHI Zhan-Zhan1( ), PANG Su2,3, WANG Yuan-Jun4, CHI Yue-Long2,3, ZHOU Qiang2,3 ), PANG Su2,3, WANG Yuan-Jun4, CHI Yue-Long2,3, ZHOU Qiang2,3 |
1. School of Artificial Intelligence, Leshan Normal University, Leshan 614000, China
2. The Engineering and Technical College, Chengdu University of Technology, Leshan 614000, China
3. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China
4. School of Land and Resources, China West Normal University, Nanchong 637002, China |
|
|
|
|
Abstract Random noise attenuation played an important role in the seismic data processing. The low-rank estimation of the seismic signal in the time-frequency domain is essentially a trace-by-trace process, which cannot exploit the channel-to-channel coherence of the signal. We propose a novel random noise attenuation based on f-x low-rank matrix approximation with nonconvex regularization. Firstly, the noisy seismic data is transformed into the f-x domain by Fourier transform. Then, the time-frequency method is employed to decompose each discrete frequency slice. Finally, we estimate the sparse low-rank matrix from the obtained noisy matrix. This method enables the denoising of non-stationary signals by exploiting the spectral differences between signal and noise. Compared with the common shot and mid-point gathers, the common offset gather is characterized by flat events, which basically satisfies the assumption of linear events for f-x domain denoising, and it is suggested that the proposed algorithm should be applied to the common offset gather. Synthetic and real data sets demonstrate the performance of our proposed method in random noise suppression and preserving more useful energy.
|
|
Received: 24 September 2021
Published: 03 January 2023
|
|
|
|
|
|
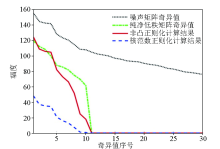
|
Comparison of standard nuclear norm and nonconvex regularizations
|
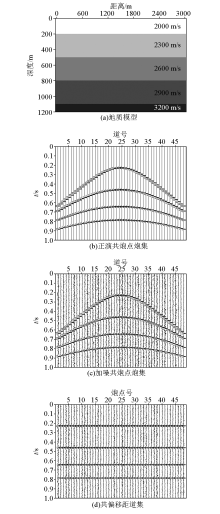
|
Geological model and seismic data forwarding
|

|
Denoised results and noise sections in the common offset gathers
|
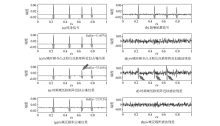
|
Comparison of the three denoising algorithms in the common offset gathers with a single trace
|
|
Comparison of denoising results of two domains in common shot gathers
|

|
Field seismic data
|
|
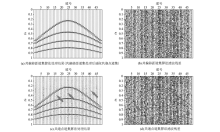
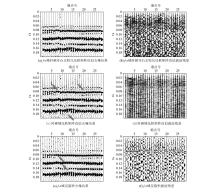
Comparison of denoising algovithms for common offset gathers of the field data
|

|
Comparison of the field data’s denoising results of the two domains in common shot gathers
|
| [1] |
Yilmaz Öz. Seismic data analysis[J]. Society of Exploration Geophysicists, 2001.
|
| [2] |
刘剑, 秦飞龙. 改进的小波阈值法及其在地震数据降噪处理中的应用[J]. 物探与化探, 2020, 44(4): 784.

|
| [2] |
Liu J, Qin F L. The application of the improved wavelet threshold method to seismic data de-noising[J]. Geophysical and Geochemical Exploration, 2020, 44(4): 784-789.

|
| [3] |
孙永壮, 李键, 秦德文, 等. 三维边缘保持滤波方法在海上地震数据噪声压制中的应用研究——以东海某凹陷为例[J]. 物探与化探, 2021, 45(3): 692-701.

|
| [3] |
Sun Y Z, Li J, Qin D W, et al. The application of 3D edge-preserving de-noising methods based on structure oriented in a complex faults block:A case study of C oilfield in East China Sea[J]. Geophysical and Geochemical Exploration, 2021, 45(3):692-701.

|
| [4] |
Rasoul A, Mokhtar M, Roshandel K A, et al. Random noise attenuation of 2D seismic data based on sparse low-rank estimation of the seismic signal[J]. Computers & Geosciences, 2020, 135:104376.

|
| [5] |
Sheriff R E, Geldart L P. Exploration seismology[M]. Cambridge: Cambridge University Press, 1995.
|
| [6] |
Canales L L. Random noise reduction[C]// 54th Annual International Meeting. Atlanta:SEG, 1984:525-572.
|
| [7] |
Chen Y K, Ma J T. Random noise attenuation by f-x empirical-mode decomposition predictive filtering[J]. Geophysics, 2014, 79(3): 81-91.
|
| [8] |
Ray A, Jon C. Lateral prediction for noise attenuation by t-x and f-x techniques[J]. Geophysics, 1995, 60(6): 1887-1896.

|
| [9] |
Maïza B, Mirko V B. Random and coherent noise attenuation by empirical mode decomposition[J]. Geophysics, 2009, 74(5): 89-98.
|
| [10] |
王亚娟, 李怀良, 庹先国, 等. 一种集成经验模态分解的样本熵阈值微地震信号降噪方法[J]. 物探与化探, 2019, 43(5): 1083-1089.

|
| [10] |
Wang Y J, Li H L, Tuo X G, et al. A denoising method for microseismic signal based on the ensemble empirical mode decomposition of sample entropy threshold[J]. Geophysical and Geochemical Exploration, 2019, 43(5): 1083-1089.

|
| [11] |
Liu W, Duan Z Y. Seismic signal denoising using f-x variational mode decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(8): 1313-1317.

|
| [12] |
Rasoul A, Roshandel K A, Mokhtar M, et al. Seismic random noise attenuation using sparse low-rank estimation of the signal in the time-frequency domain[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(5): 1612-1618.
|
| [13] |
Cai H P, He Z H, Huang D J. Seismic data denoising based on mixed time-frequency methods[J]. Applied Geophysics, 2011, 8(4): 319-327.

|
| [14] |
Amir N S M, Saman G, Roshandel K A, et al. Sparse time-frequency representation for seismic noise reduction using low-rank and sparse decomposition[J]. Geophysics, 2016, 81(2): 117-124.
|
| [15] |
Oliveira M S, Henriques M V C, Leite F E A, et al. Seismic denoising using curvelet analysis[J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(5): 2106-2110.

|
| [16] |
Deng L, Yuan S Y, Wang S X. Sparse bayesian learning-based seismic denoise by using physical wavelet as basis functions[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 1993-1997.

|
| [17] |
Bing P P, Liu W, Zhang Z H. A robust random noise suppression method for seismic data using sparse low-rank estimation in the time-frequency domain[J]. IEEE Access, 2020, 8: 183546-183556.

|
| [18] |
Gao J J, Aaron S, Sacchi M D. Parallel matrix factorization algorithm and its application to 5D seismic reconstruction and denoising[J]. Geophysics, 2015, 80(6): 173-187.
|
| [19] |
Nadia K, Sacchi M D. A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation[J]. Geophysics, 2012, 77(3): 113-122.
|
| [20] |
Xu P C, Lu W K, Wang B F. Seismic interference noise attenuation by convolutional neural network based on training data generation[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(4): 741-745.

|
| [21] |
Yu S W, Ma J W, Wang W L. Deep learning for denoising[J]. Geophysics, 2019, 84(6): 333-350.
|
| [22] |
Zhang M, Liu Y, Chen Y K. Unsupervised seismic random noise attenuation based on deep convolutional neural network[J]. IEEE Access, 2019, 7: 179810-179822.
|
| [23] |
梁立锋, 刘秀娟, 张宏兵, 等. 超参数对GRU-CNN混合深度学习弹性阻抗反演影响研究[J]. 物探与化探, 2021, 45(1): 133-139.

|
| [23] |
Liang L F, Liu X J, Zhang H B, et al. A study of the effect of hyperparameters GRU-CNN hybrid deep learning EI inversion[J]. Geophysical and Geochemical Exploration, 2021, 45(1): 133-139.

|
| [24] |
Meng F L, Fan Q Y, Li Y. Self-supervised learning for seismic data reconstruction and denoising[J]. IEEE Geoscience and Remote Sensing Letters, 2021: 1-5.
|
| [25] |
Stephen A. Generative adversarial networks in seismic data processing[M]// Society of Exploration Geophysicists, 2018:1991-1995.
|
| [26] |
Vicente O, Mauricio S. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis[J]. Geophysics, 2011, 76(3): 25-32.
|
| [27] |
Chen Y K, Zhou Y T, Chen W, et al. Empirical low-rank approximation for seismic noise attenuation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8): 4696-4711.

|
| [28] |
Cai J F, Candès E J, Shen Z W. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982.

|
| [29] |
Ankit P, Selesnick I W. Enhanced low-rank matrix approximation[J]. IEEE Signal Processing Letters, 2016, 23(4): 493-497.

|
| [30] |
Lu C Y, Zhu C M, Xu C Y, et al. Generalized singular value thresholding[J]. arXiv e-prints, 2015,(12).
|
| [31] |
Rick C. Nonconvex splitting for regularized low-rank+sparse decomposition[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5810-5819.

|
| [32] |
Gu S H, Zhang L, Zuo W M, et al. Weighted nuclear norm minimization with application to image denoising[C]// 2014 IEEE Conference on Computer Vision and Pattern recognition, 2014.
|
| [33] |
Zhang S A, Yin P H, Xin J. Transformed schatten-1 iterative thresholding algorithms for low rank matrix completion[J]. arXiv e-prints, 2015: 1506-4444.
|
| [34] |
Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627.

|
| [35] |
Ewout V B, Michael P F. Probing the pareto frontier for basis pursuit solutions[J]. Siam J. Sci. Comput., 2008, 31(2): 890-912.

|
|
|
|

