|
|
|
| Joint Euler deconvolution of multi-component gravity gradient data and software design |
SUN Bo-Xuan1( ), HOU Zhen-Long1( ), HOU Zhen-Long1( ), Zhou Wen-Yue2, GONG En-Pu1, Zheng Yu-Jun1, CHENG Hao1 ), Zhou Wen-Yue2, GONG En-Pu1, Zheng Yu-Jun1, CHENG Hao1 |
1. School of Resources and Civil Engineering, Northeastern University, Shenyang 110819, China
2. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China |
|
|
|
|
Abstract Compared with Euler deconvolution, joint Euler deconvolution of multi-component gravity gradient data features higher calculation accuracy and inversion resolution. To eliminate the divergent solutions of calculation, different screening methods must be used in the application of joint Euler deconvolution of multi-component gravity gradient data, making the calculation process cumbersome. It is evident that effective screening methods and developing a piece of easy-to-use and visual software can improve the accuracy, convenience, and effects of the joint Euler deconvolution of multi-component gravity gradient data. Therefore, this study proposed the joint Euler deconvolution of gravity gradient data with the constraint of edge detection based on correlation coefficients. Moreover, on the design principles of the intuitive interfaces, practical functions, and concise codes, this study designed a software system with functions such as data/file management, two-dimensional/three-dimensional visualization, edge detection, and joint Euler deconvolution of multi-component gravity gradient data using Python language and its function library to meet the requirements of algorithm flow and functions. The accuracy of calculations and the practicability of the software have been verified through a theoretical model and tests of measured data, proving that the software designed in this study can improve the application effects.
|
|
Received: 03 September 2021
Published: 03 January 2023
|
|
|
|
Corresponding Authors:
HOU Zhen-Long
E-mail: 960143992@qq.com;houzhenlong@mail.neu.edu.cn
|
|
|
|

|
Visualization of edge detection results(the red wireframe in the figure indicates the boundary of the cube)
a—THDR; b—EDT; c—ASM; d—EEDT; e—NEDT; f—TILT
|
|
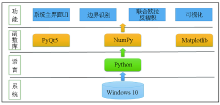
Software architecture diagram
|

|
Main interface of software
|
|
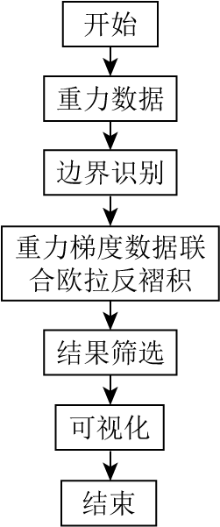
Flow chart of algorithm
|
|
File preview window
|
|
Data operation window
|
|
Window of file storage path selection
|
|
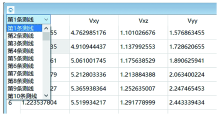
Line switching window
|
|
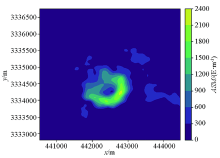
Edge detection result diagram from software
|
|
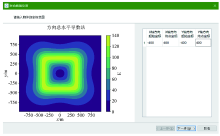
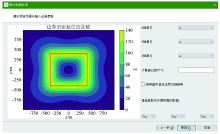
Delimit the geological body range input interface
|
|
Joint Euler deconvolution of multiple gravity gradiometry tensors calculation parameters input interface
|
|
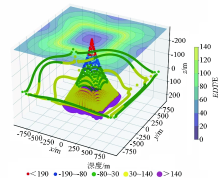
Preliminary calculation results of joint Euler deconvolution of multiple gravity gradiometry tensors
|
|
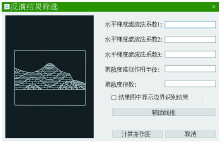
Results filtering standard input interface
|
|
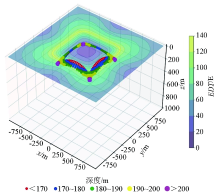
Visualization of joint Euler deconvolution of multiple gravity gradiometry tensors results
|

|
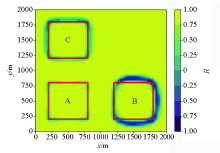
Contour figure of gravity data and gravity gradient data(the red wireframe in the figure indicates the boundary of the cube)
|
|
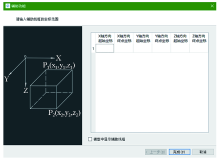
Auxiliary wireframe coordinate input interface
|

| 模型 | 中心位置/
(m,m,m) | 尺寸大小/
(m,m,m) | 剩余密度/
(g·cm-3) | | A | 1500, 500, 150 | 600×600×100 | 1 | | B | 500, 1500, 450 | 600×600×100 | 1 | | C | 500, 500, 750 | 600×600×100 | 1 |
|
|
|
|
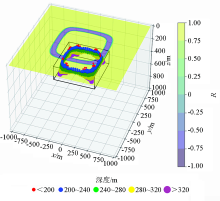
Visualization of edge detection(the red wireframe in the figure indicates the boundary of the cube)
|
|
Screened results of joint Euler deconvolution of multiple gravity gradiometry tensors
|

|
Calculation results of joint Euler deconvolution of multiple gravity gradiometry tensors of Vinton Dome data
a—3D display; b—z-direction view
|
| [1] |
Hou Z L, Wei X H, Huang D N. Fast density inversion solution for full tensor gravity gradiometry data[J]. Pure and Applied Geophysics, 2016, 173(2): 509-523.

|
| [2] |
汤井田, 史庆斌, 胡双贵, 等. 基于重力梯度张量曲率的边界识别[J]. 地球物理学报 2019, 62(5):1872-1884.
|
| [2] |
Tang J T, Shi Q B, Hu S G, et al. Edge detection based on curvature of gravity gradient tensors[J]. Chinese Journal of Geophysics, 2019, 62(5): 1872-1884.
|
| [3] |
张琦. 重力梯度数据的边界识别与深度成像方法研究[D]. 长春: 吉林大学, 2019.
|
| [3] |
Zhang Q. The study on edge detection and depth imaging method for gravity gradient data[D]. Changchun: Jilin University, 2019.
|
| [4] |
郑玉君, 侯振隆, 巩恩普, 等. 基于深度加权的多分量重力梯度数据联合相关成像方法[J]. 吉林大学学报:地球科学版, 2020, 50(4):1197-1210.
|
| [4] |
Zheng Y J, Hou Z L, Gong E P, et al. Correlation imaging method with joint multiple gravity gradiometry data based on depth weighting[J]. Journal of Jilin University:Earth Science Edition, 2020, 50(4): 1197-1210.
|
| [5] |
Thompson D T. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47(1): 31-37.

|
| [6] |
Cooper G R J. Euler Deconvolution with improved accuracy and multiple different structural indices[J]. Journal of China University of Geosciences, 2008, 19(1):72-76.

|
| [7] |
Petar S, Alan R. Euler deconvolution of gravity anomalies from thick contact/fault structures with extended negative structural index[J]. Society of Exploration Geophysicists, 2010, 75(6): 151-158.
|
| [8] |
Wang J, Meng X H, Li F. New improvements for lineaments study of gravity data with improved Euler inversion and phase congruency of the field data[J]. Journal of Applied Geophysics, 2017, 136: 326-334.

|
| [9] |
Eric N N, Koumetio F, Victor J, et al. Gravity study of the Douala sub-basin (Cameroon) using Euler 3D deconvolution, source edge detection (SED) and special function analysis[J]. SN Applied Sciences, 2019, 1(10): 1-17.

|
| [10] |
Zhang C, Mushayandebvu M F, Reid A B, et al. Euler deconvolution of gravity tensor gradient data[J]. Geophysics, 2000, 65(2): 512-520.

|
| [11] |
Majid B, Laust B P. Eigenvector analysis of gravity gradient tensor to locate geologic bodies[J]. Geophysics, 2010, 75(6): 137-149.
|
| [12] |
周文月, 陈昌昕, 侯振隆, 等. 不同高度数据联合欧拉反褶积法研究[J]. 地球物理学报, 2018, 61(8):3400-3409.
|
| [12] |
Zhou W Y, Chen C X, Hou Z L, et al. The study on the joint Euler deconvolution method of different heights[J]. Chinese Journal of Geophysics, 2018, 61(8): 3400-3409.
|
| [13] |
侯振隆, 王恩德, 周文纳, 等. 重力梯度欧拉反褶积及其在文顿盐丘的应用[J]. 石油地球物理勘探, 2019, 54(2):472-479.
|
| [13] |
Hou Z L, Wang E D, Zhou W N, et al. Euler deconvolution of gravity gradiometry data and the application in Vinton Dome[J]. Oil Geophysical Prospecting, 2019, 54(2): 472-479.
|
| [14] |
马国庆, 吴琪, 李丽丽. 重力梯度张量联合欧拉反褶积法研究[J]. 地球物理学进展, 2020, 35(6):2188-2193.
|
| [14] |
Ma G Q, Wu Q, Li L L. Study on the joint Euler deconvolution method of gravity gradient tensor data[J]. Progress in Geophysics, 2020, 35(6): 2188-2193.
|
| [15] |
王林飞, 薛典军, 何辉, 等. 插件技术在GeoProbe地球物理软件平台中的应用[J]. 物探与化探, 2013, 37(3):547-551.
|
| [15] |
Wang L F, Xue D J, He H, et al. The application of the plug-in technology to geophysical software platform (GeoProbe)[J]. Geophysical and Geochemical Exploration, 2013, 37(3): 547-551.
|
| [16] |
Norman S N, James C. Seismic image undersampling-resolution, visibility, and display[J]. Society of Exploration Geophysicists, 2017, 37(1): 37-45.
|
| [17] |
詹毅, 徐少波, 雷娜, 等. 国产大型地震数据处理解释一体化软件GeoEast推广应用实践[J]. 石油科技论坛, 2020, 39(1):67-71.
|
| [17] |
Zhan Y, Xu S B, Lei N, et al. Promote application of GeoEast-large-scale domestic seismic data processing and interpretation integrated software[J]. Oil Forum, 2020, 39(1): 67-71.
|
| [18] |
郑元满, 姚长利, 李泽林, 等. 重磁处理解释系统软件设计与关键实现技术[J]. 地球物理学报, 2019, 62(10):3744-3759.
|
| [18] |
Zheng Y M, Yao C L, Li Z L, et al. Software design and key implementation techniques of gravity and magnetic processing and interpretation system[J]. Chinese Journal of Geophysics, 2019, 62(10): 3744-3759.
|
| [19] |
陈靖, 王万银, 郭文波, 等. 重磁软件架构设计及实现方案研究[J]. 物探与化探, 2020, 44(4):905-913.
|
| [19] |
Chen J, Wang W Y, Guo W B, et al. A study of the design and implementation of gravity and magnetic software[J]. Geophysical and Geochemical Exploration, 2020, 44(4): 905-913.
|
| [20] |
王浩然. 基于并行计算与深度学习算法的大规模重磁数据反演研究[D]. 长春: 吉林大学, 2020.
|
| [20] |
Wang H R. The study on the gravity and magnetic inversion based on parallel computing and deep learning algorithm[D]. Changchun: Jilin University, 2020.
|
| [21] |
张浩平, 付媛媛. VC++调用Matlab实现三维欧拉反褶积运算[J]. 物探化探计算技术, 2006, 28(2):178-181,88.
|
| [21] |
Zhang H P, Fu Y Y. Implementation of 3-D Euler disconvolution by VC++ Calling Matlab[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2006, 28(2): 178-181,88.
|
| [22] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.
|
| [22] |
Guan Z N. Geomagnetic field and magnetic exploration[M]. Beijing: Geological Publishing House, 2005.
|
| [23] |
Miller H G, Singh V. Potential field Tilt-A new concept for location of potential field sources[J]. Journal of Applied Geophysics, 1994, 32: 213-217.

|
| [24] |
Guo C W, Xing Z, Wang L F, et al. Three-directional analytic signal analysis and interpretation of magnetic gradient tensor[J]. Applied Geophysics, 2020, 17(2): 285-296.

|
| [25] |
王万银. 位场总水平导数极值位置空间变化规律研究[J]. 地球物理学报, 2010, 53(9):2257-2270.
|
| [25] |
Wang W Y. Spatial variation law of the extreme value positions of total horizontal derivative for potential field data[J]. Chinese Journal of Geophysics, 2010, 53(9): 2257-2270.
|
| [26] |
Wang W Y, Pan Y, Qiu Z Y. A new edge recognition technology based on the normalized vertical derivative of the total horizontal derivative for potential field data[J]. Applied Geophysics, 2009, 6(3): 226-233.

|
| [27] |
袁园, 黄大年, 余青露. 利用加强水平方向总水平导数对位场全张量数据进行边界识别[J]. 地球物理学报, 2015, 58(7):2556-2565.
|
| [27] |
Yuan Y, Huang D N, Yu Q L. Using enhanced directional total horizontal derivatives to detect the edge of potential-field full tensor data[J]. Chinese Journal of Geophysics, 2015, 58(7): 2556-2565.
|
| [28] |
侯振隆, 王恩德, 唐水亮, 等. 方向总水平导数法的改进和边界识别中的应用[J]. 东北大学学报:自然科学版, 2019, 40(1):104-108.
|
| [28] |
Hou Z L, Wang E D, Tang S L, et al. Improvements of the directional total horizontal derivatives and their application in edge detection[J]. Journal of Northeastern University:Natural Science, 2019, 40(1): 104-108.
|
| [29] |
秦朋波. 重力和重力梯度数据联合反演方法研究[D]. 长春: 吉林大学, 2016.
|
| [29] |
Qin P B. A study on integrated gravity and gravity gradient data in inversion[D]. Changchun: Jilin University, 2016.
|
| [30] |
高秀鹤. 重磁及张量梯度数据三维反演方法研究与应用[D]. 长春: 吉林大学, 2019.
|
| [30] |
Gao X H. The study and application of 3D inversion methods gravity & magnetic their gradient tensor data[D]. Changchun: Jilin University, 2019.
|
| [31] |
周文月. 重磁张量场源空间分布特征反演技术研究[D]. 长春: 吉林大学, 2019.
|
| [31] |
Zhou W Y. Research on inversion technique of distribution characteristics of gravity and magnetic tensor field sources[D]. Changchun: Jilin University, 2019.
|
| [1] |
CHEN Qing, SUN Shuai, DING Cheng-Yi, HUANG Xiao-Yu, CHEN Hao, SHEN Peng, LUO Gang, WEI Yao-Cong. Application of iTilt-Euler deconvolution in gravity data processing and fault system interpretation[J]. Geophysical and Geochemical Exploration, 2021, 45(6): 1578-1587. |
| [2] |
LI Yao, ZHANG Xiao-Jie, LIU Gong-Li, GONG Min. The prediction of Archean buried hill fracture reservoir in BZ-A structure of the Bohai oilfield[J]. Geophysical and Geochemical Exploration, 2021, 45(1): 37-45. |
|
|
|
|

