|
|
|
| Inversion of Rayleigh wave dispersion curves based on the improved sparrow search algorithm |
SUN Xu1( ), JI Zi-Qi2( ), JI Zi-Qi2( ), YANG Qing-Yi1, LIU Bo-Zheng1 ), YANG Qing-Yi1, LIU Bo-Zheng1 |
1. Shandong Electric Power Engineering Consulting Institute Co.,Ltd.,Jinan 250014,China
2. Institute of Geophysics & Geomatics,China University of Geosciences (Wuhan),Wuhan 430074,China |
|
|
|
|
Abstract Nonlinear optimization algorithms can be used to conduct a global search for the optimal solutions within a given parameter range, inherently making them highly competent in performing a global search and escaping from local extrema.In this study,an emerging nonlinear optimization algorithm-the sparrow search algorithm (SSA) was introduced for the inversion of Rayleigh wave dispersion curves.To address the problems of multiple parameters and local extrema, adaptive t-distribution was introduced.The data acquired from the inversion experiment of three theoretical models indicate that the improved SSA has high inversion accuracy,stability,and resistance to random noise compared with the conventional SSA.Furthermore,the improved SSA can yield better performance than particle swarm optimization and differential evolution algorithm due to its capability to achieve a more reasonable balance between the early global search and late local search in the process of iteration.
|
|
Received: 07 September 2021
Published: 03 January 2023
|
|
|
|
Corresponding Authors:
JI Zi-Qi
E-mail: sunxu@sdepci.com;16602715396@163.com
|
|
|
|

层
序
号 | 模型参数 | 搜索范围 | 横波
速度/
(m·s-1) | 纵波
速度/
(m·s-1) | 密度/
(g·cm-3) | 层厚
度/m | 横波
速度/
(m·s-1) | 层厚
度/m | | 1 | 200 | 663 | 1.7 | 2 | 100~300 | 1~3 | | 2 | 300 | 995 | 1.8 | 4 | 150~450 | 2~6 | | 3 | 400 | 1327 | 1.9 | 6 | 200~600 | 3~9 | | 4 | 500 | 1658 | 2.0 | ∞ | 250~750 | ∞ |
|
Parameters and search range of four layer speed increasing model (model A)
|

层
序
号 | 模型参数 | 搜索范围 | 横波
速度/
(m·s-1) | 纵波
速度/
(m·s-1) | 密度/
(g·cm-3) | 层厚
度/m | 横波
速度/
(m·s-1) | 层厚
度/m | | 1 | 300 | 995 | 1.8 | 2 | 150~450 | 1~3 | | 2 | 200 | 663 | 1.7 | 4 | 100~300 | 2~6 | | 3 | 400 | 1327 | 1.9 | 6 | 200~600 | 3~9 | | 4 | 500 | 1658 | 2.0 | ∞ | 250~750 | ∞ |
|
Parameters and search range of four layer model with low velocity interlayer(model B)
|

层
序
号 | 模型参数 | 搜索范围 | 横波
速度/
(m·s-1) | 纵波
速度/
(m·s-1) | 密度/
(g·cm-3) | 层厚
度/m | 横波
速度/
(m·s-1) | 层厚
度/m | | 1 | 200 | 663 | 1.7 | 2 | 100~300 | 1~3 | | 2 | 400 | 1327 | 1.9 | 4 | 200~600 | 2~6 | | 3 | 300 | 995 | 1.8 | 6 | 150~450 | 3~9 | | 4 | 500 | 1658 | 2.0 | ∞ | 250~750 | ∞ |
|
Parameters and search range of four storey model with high-speed interlayer (model C)
|
|
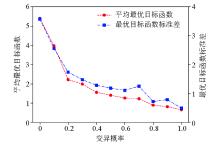
Effect of mutation probability on inversion performance of improved algorithm
|
|
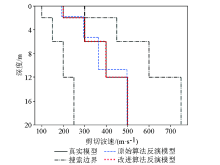
Original algorithm and improved algorithm model of model A
|
|
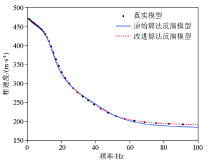
Dispersion curve of original algorithm and improved algorithm of model A
|

| 参数 | 传统算法 | 改进算法 | | 反演均值 | 相对误差/% | 标准差 | 反演均值 | 相对误差/% | 标准差 | | vs1/(m·s-1) | 192.15 | 3.92 | 18.48 | 200.07 | 0.04 | 0.58 | | vs2/(m·s-1) | 295.83 | 1.39 | 44.30 | 299.91 | 0.03 | 1.55 | | vs3/(m·s-1) | 364.19 | 8.95 | 59.81 | 399.72 | 0.07 | 1.94 | | vs4/(m·s-1) | 498.00 | 0.40 | 5.33 | 500.07 | 0.02 | 1.52 | | h1/m | 1.79 | 10.60 | 0.60 | 2.00 | 0.19 | 0.02 | | h2/m | 3.49 | 12.66 | 1.25 | 4.00 | 0.13 | 0.04 | | h3/m | 5.42 | 9.68 | 1.76 | 5.99 | 0.21 | 0.06 |
|
Statistics of inversion results of model A
|
|
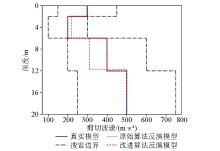
Inversion model of model B
|
|
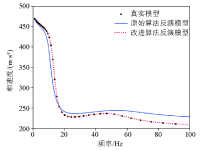
Dispersion curve of inversion model of model B
|
|
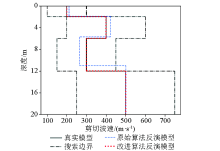
Inversion model of model C
|
|
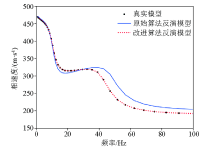
Dispersion curve of inversion model of model C
|

| 参数 | 传统算法 | 改进算法 | | 反演均值 | 相对误差/% | 标准差 | 反演均值 | 相对误差/% | 标准差 | | vs1/(m·s-1) | 293.44 | 2.19 | 64.94 | 300.35 | 0.12 | 2.90 | | vs2/(m·s-1) | 218.18 | 9.09 | 26.81 | 200.29 | 0.15 | 0.92 | | vs3/(m·s-1) | 309.04 | 22.74 | 88.99 | 399.97 | 0.01 | 3.89 | | vs4/(m·s-1) | 499.01 | 0.20 | 4.41 | 500.39 | 0.08 | 1.86 | | h1/m | 2.05 | 2.29 | 0.54 | 1.99 | 0.41 | 0.06 | | h2/m | 3.97 | 0.64 | 1.14 | 4.01 | 0.14 | 0.06 | | h3/m | 5.66 | 5.62 | 1.88 | 6.06 | 1.05 | 0.36 |
|
Statistics of inversion results of model B
|

| 参数 | 传统算法 | 改进算法 | | 反演均值 | 相对误差/% | 标准差 | 反演均值 | 相对误差/% | 标准差 | | vs1/(m·s-1) | 211.19 | 5.60 | 31.14 | 200.01 | 0.00 | 1.05 | | vs2/(m·s-1) | 422.60 | 5.65 | 76.77 | 399.90 | 0.03 | 2.23 | | vs3/(m·s-1) | 264.21 | 11.93 | 60.28 | 299.99 | 0.00 | 1.59 | | vs4/(m·s-1) | 501.12 | 0.22 | 7.05 | 500.14 | 0.03 | 2.61 | | h1/m | 1.92 | 4.22 | 0.30 | 2.00 | 0.05 | 0.01 | | h2/m | 3.81 | 4.66 | 0.61 | 4.00 | 0.03 | 0.02 | | h3/m | 5.27 | 12.17 | 1.47 | 6.00 | 0.01 | 0.03 |
|
Statistics of inversion results of model C
|
|
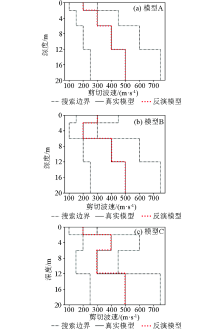
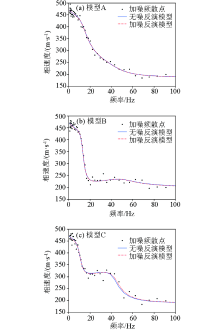
Inversion model with noise
|
|
Inversion results of geological model with or without noise
|

| 模型 | 参数 | 反演均值/(m·s-1) | 相对误差/% | 标准差/(m·s-1) | | 模型A | vs1 | 199.70 | 0.15 | 1.64 | | vs2 | 299.07 | 0.31 | 2.21 | | vs3 | 400.18 | 0.05 | 4.49 | | vs4 | 499.33 | 0.13 | 1.88 | | h1 | 1.98 | 0.88 | 0.07 | | h2 | 4.00 | 0.06 | 0.06 | | h3 | 6.05 | 0.80 | 0.35 | | 模型B | vs1 | 301.03 | 0.34 | 10.48 | | vs2 | 199.26 | 0.37 | 1.81 | | vs3 | 402.53 | 0.63 | 10.56 | | vs4 | 499.18 | 0.17 | 1.35 | | h1 | 2.00 | 0.05 | 0.08 | | h2 | 3.97 | 0.64 | 0.06 | | h3 | 5.95 | 0.79 | 0.19 | | 模型C | vs1 | 200.04 | 0.02 | 2.15 | | vs2 | 398.92 | 0.27 | 5.96 | | vs3 | 297.72 | 0.76 | 4.94 | | vs4 | 499.37 | 0.13 | 2.12 | | h1 | 1.95 | 2.55 | 0.05 | | h2 | 3.92 | 1.89 | 0.10 | | h3 | 5.95 | 0.92 | 0.14 |
|
Statistics of inversion results of three geological models under noise conditions
|

|
Optimal objective function curve and average optimal objective function curve of 30 inversions
a—original sparrow search algorithm;b—particle swarm optimization;c—differential evolution algorithm;d—improved sparrow search algorithm
|

| 算法 | 原始麻雀
搜索算法 | 粒子群
算法 | 差分进
化算法 | 改进麻雀
搜索算法 | | 平均最优目标函数 | 4.85 | 1.64 | 1.08 | 0.85 | | 最优目标函数标准差 | 1.79 | 2.22 | 0.42 | 0.71 | | 平均相对误差/% | 7.16 | 4.47 | 5.47 | 0.27 | | 平均相对标准差/% | 19.45 | 22.17 | 13.76 | 1.88 |
|
Inversion performance statistics of different algorithms
|

| 层序 | 层底深度/m | 地层描述 | | 1 | 0.6 | 素填土:黄褐色,成分主要为黏性土,混少量碎石、煤渣,该层土工程性质极不均一,素填土 | | 2-1 | 2.65 | 粉土:黄褐,稍密—中密,湿—很湿,具触变性,夹粉质黏土、黏土 | | 2-2 | 4.15 | 粉土:黄褐,稍密—中密,湿—很湿,具触变性,夹粉质黏土、黏土、细砂薄层 | | 3-1 | 8.3 | 粉质黏土:黄褐、褐黄等色,可塑状态为主,局部为软塑状态,很湿,夹粉质黏土薄层,含铁锰质结核、有机质及螺壳碎片,混少量小姜石 | | 4-1 | 9.8 | 黏土:灰黑、深灰色,可塑状态为主,局部软塑状态,很湿,含铁锰质结核、螺壳碎片,混粉粒及少量小姜石 | | 4-2 | 11.85 | 黏土:灰黑、深灰色、灰绿等色,硬塑—坚硬状态为主,局部为可塑状态,饱和,夹粉土、粉细砂、中粗砂薄层或透镜体,混姜石 | | 5-1 | 14.65 | 粉细砂:浅黄、黄褐等色,成分为石英、长石,稍密—中密为主,局部松散—稍密,饱和, 混黏性土10%~20%左右,夹粉土薄层 | | 5-2 | 19.9 | 粉细砂:浅黄、黄褐等色,成分为石英、长石,中密—密实为主,局部松散—稍密,饱和,混少量黏性土 | | 5-3 | 3.5 | 粉粗砂:褐黄、黄褐等色,成分为石英、长石,稍密—中密为主,局部松散,饱和,局部相变为中砂、粗砂 |
|
Description of the K41 drill of work area
|

| 层序号 | 模型参数搜索范围 | 横波速度/
(m·s-1) | 泊松比 | 密度/
(g·cm-3) | 层厚
度/m | | 1 | 50~200 | 0.45 | 1.7 | 1~7 | | 2 | 100~400 | 0.45 | 1.8 | 1~7 | | 3 | 150~600 | 0.45 | 1.9 | 1~7 | | 4 | 200~800 | 0.45 | 2.0 | ∞ |
|
Parameters and search range of model
|

| 层序号 | 横波速度/(m·s-1) | 厚度/m | | 1 | 131.88 | 3.77 | | 2 | 205.22 | 4.97 | | 3 | 258.91 | 4.10 | | 4 | 461.91 | +∞ |
|
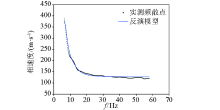
Statistics of inversion results of measured data
|
|
Inversion results of measured data
|
| [1] |
杨成林. 瑞利波法勘探原理及其应用[J]. 物探与化探, 1989, 13(6):465-468.
|
| [1] |
Yang C L. The principle and application of Rayleigh wave exploration method[J]. Geophysical and Geochemical Exploration, 1989, 13(6):465-468.
|
| [2] |
Xia J, Miller R D, Park C B. Estimation of nearsurface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 1999, 64(3): 691-700.

|
| [3] |
祁生文, 孙进忠, 何华. 瑞利波勘探的研究现状及展望[J]. 地球物理学进展, 2002, 17(4):630-662.
|
| [3] |
Qi S W, Sun J Z, He H. Research status and prospect of Rayleigh wave exploration[J]. Progress in Geophysics, 2002, 17(4):630-662.
|
| [4] |
林志平, 林俊宏, 吴柏林, 等. 浅地表地球物理技术在岩土工程中的应用与挑战[J]. 地球物理学报, 2015, 58(8):2664-2680.
|
| [4] |
Lin Z P, Lin J H, Wu B L, et al. Applications and challenges of near surface geophysics in geotechnical engineering[J]. Journal of Geophysics, 2015, 58(8):2664-2680.
|
| [5] |
崔建文. 一种改进的全局优化算法及其在面波频散曲线反演中的应用[J]. 地球物理学报, 2004, 47(3):521-527.
|
| [5] |
Cui J W. An improved global optimization method and its application to the inversion of surface wave dispersion curves[J]. Chinese Journal of Geophysics, 2004, 47(3):521-527.
|
| [6] |
蒋婵君, 周竹生, 敬荣中, 等. 遗传算法在瑞雷面波勘探中的应用[J]. 物化探计算技术, 2010, 32(5):455-513.
|
| [6] |
Jiang C J, Zhou Z S, Jing R Z, et al. Application of Genetic Algorithm in Rayleigh wave exploration[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2010, 32(5):455-513.
|
| [7] |
晋思, 邵嘉琪, 支剑丽, 等. 遗传算法在瑞利波频散曲线反演中的应用研究[J]. 人民长江, 2015, 46(3):31-33.
|
| [7] |
Jin S, Shao J Q, Zhi J L, et al. Application of Genetic Algorithm in inversion of Rayleigh wave dispersion curves[J]. Yangtze River, 2015, 46(3):31-33.
|
| [8] |
彭刘亚, 任川. 基于粒子群算法的瑞利波频散曲线反演研究[J]. 地球物理学进展, 2018, 33(4):1682-1686.
|
| [8] |
Peng L Y, Ren C. Inversion of Rayleigh wave dispersion curve using Particle Swarm Optimization algorithm[J]. Progress in Geophysics, 2018, 33(4): 1682-1686.
|
| [9] |
蔡伟, 宋先海, 袁士川, 等. 利用粒子群优化算法快速、稳定反演瑞利波频散曲线[J]. 石油地球物理勘探, 2018, 53(1):4-34.
|
| [9] |
Cai W, Song X H, Yuan S C, et al. Fast and stable inversion of Rayleigh wave dispersion curve using particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2018, 53(1): 4-34.
|
| [10] |
张晓煜, 李向. 基于粒子群算法的地震预报方法研究[J]. 地震工程学报, 2014, 36(1):69-74.
|
| [10] |
Zhang X Y, Li X. Earchquake prediction method based on Particle Swarm Optimization[J]. China Earthquake Engineering Journal, 2014, 36(1): 69-74.
|
| [11] |
杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6):1172-1227.
|
| [11] |
Yang B, Xiong Z Q, Zhang D Z, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1172-1227.
|
| [12] |
程飞, 刘江平, 毛茂, 等. 参数自适应差分演化算法在面波频散曲线反演中的应用[J]. 岩土工程学报, 2016, 38(1):147-154.
|
| [12] |
Cheng F, Liu J P, Mao M, et al. Self-adapting control parameters-based Differential Evolution Algorithm for inversion of Rayleigh wave dispersion curves[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 147-154.
|
| [13] |
于东凯, 宋先海, 张学强, 等. 蚱蜢算法在瑞利波频散曲线反演中的应用[J]. 石油地球物理勘探, 2019, 54(2):236-301.
|
| [13] |
Yu D K, Song X H, Zhang X Q, et al. Rayleigh wave dispersion inversion based on grasshopper optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(2): 236-301.
|
| [14] |
王天琦, 于东凯, 蔡润. 基于改进蚁群算法在面波频散曲线反演中的应用[J]. 地震工程学报, 2020, 42(6):1523-1533.
|
| [14] |
Wang T Q, Yu D K, Cai R. Application of the improved ant colony algorithm in the inversion of Rayleigh wave dispersion curves[J]. China Earthquake Engineering Journal, 2020, 42(6): 1523-1533.
|
| [15] |
Xue J K, Shen B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
|
|
|
|

