|
|
|
| Optimization of interpolation parameters for 1∶50 000 regular distribution gravity data based on radial basis function |
XU Hai-Hong1,2( ), HAN Xiao-Feng1,2( ), HAN Xiao-Feng1,2( ), YUAN Bing-Qiang3, ZHANG Chun-Guan3, WANG Bao-Wen1,2, ZHAO Fei1,2, DUAN Rui-Feng4 ), YUAN Bing-Qiang3, ZHANG Chun-Guan3, WANG Bao-Wen1,2, ZHAO Fei1,2, DUAN Rui-Feng4 |
1. Xi’an Center of Geological Survey, China Geological Survey, Xi’an 710054, China
2. Key Laboratory of Paleozoic Oil and Gas Geology in North China, Xi’an 710054, China
3. School of Earth Sciences and Engineering, Xi’an Shiyou University, Xi’an 710065, China
4. Shaanxi Geo-mining Geophysical and Geochemical Exploration Team Co. Ltd.,Xi’an 710043, China |
|
|
|
|
Abstract In order to select the optimized interpolation parameters of 1∶50 000 regular distribution gravity data to provide quantitative interpolation basis for data gridding. We take the gravity data of the theoretical model as an example, use the radial basis function method to optimize the interpolation parameters, such as the interpolation kernel function and the search neighborhood, and using the standard deviationindex to evaluate the interpolation results corresponding to different parameters. The results indicate that the natural cubic spline kernel function corresponds to the highest interpolation accuracy, when the R2 parameter is in the first interval (0~1), the interpolation is stable and accurate. The interpolation accuracy is highest when the search neighborhood is elliptical, and the preferred interpolation parameters are as follows: the search radius R1=3 km, R2=4.5 km, the number of sectors to search is 4, the search angle is 32°, the anisotropy ratio is 0.667, the anisotropy angle is 32°, the maximum number of data to use from all sectors is 80, the maximum number of data to use from each sector is 20, the minimum number of data in all sectors (node is blanked if fewer) is 8, the node is blanked if more than 3 sectors are empty.
|
|
Received: 09 February 2021
Published: 21 December 2021
|
|
|
|
Corresponding Authors:
HAN Xiao-Feng
E-mail: honghaibeibei@163.com;daijiadj@163.com
|
|
|
|

模型
编号 | (x,y)角点坐标/m | 顶面埋
深/m | 底面埋
深/m | 密度差
/(g·cm-3) | | 1 | (5104,16963);(3736,16963);(17,13939);(17,12520) | 500 | 1500 | 0.6 | | 2 | (10691,16927);(9092,16927);(4514,11690);(5642,11300) | 600 | 2600 | 0.6 | | 3 | (5750,11259);(4669,11631);(2889,10576);(41,9582);(41,8278);(3152,9324) | 600 | 2600 | 0.6 | | 4 | (15271,16969);(13632,16969);(9272,11182);(10803,10968) | 800 | 3000 | 0.5 | | 5 | (10951,10934);(9419,11152);(5412,8185);(39,5461);(39,3982);(6094,7051) | 800 | 3000 | 0.5 | | 6 | (16972,13434);(16972,14379);(13395,10836);(14274,10796) | 600 | 2100 | 0.5 | | 7 | (14326,10770);(13576,10811);(8905,6189);(1616,307);(4525,1783);(9646,5535) | 600 | 2100 | 0.5 | | 8 | (16954,5371);(16954,7963);(1155,36);(5574,36) | 900 | 3400 | 0.4 |
|
Parameters of the theoretical model
|

|
The model (a) and its theoretical gravity anomaly (b)
|

|
Residual results and curve of the five kernel functions
|

| R2 | 标准偏差 | R2 | 标准偏差 | R2 | 标准偏差 | R2 | 标准偏差 | | 0 | 0.014886 | 2 | 0.014985 | 20 | 0.033150 | 200 | 0.187007 | | 0.018 | 0.014855 | 3 | 0.014956 | 30 | 0.040566 | 300 | 0.200942 | | 0.1 | 0.014847 | 4 | 0.014869 | 40 | 0.043862 | 400 | 0.208563 | | 0.2 | 0.014857 | 5 | 0.014919 | 50 | 0.046008 | 500 | 0.217865 | | 0.3 | 0.014870 | 6 | 0.015109 | 60 | 0.046918 | 600 | 0.220763 | | 0.4 | 0.014882 | 7 | 0.015389 | 70 | 0.050115 | 700 | 0.223089 | | 0.5 | 0.014893 | 8 | 0.015562 | 80 | 0.051539 | 800 | 0.223366 | | 0.6 | 0.014903 | 9 | 0.015653 | 90 | 0.054638 | 900 | 0.225889 | | 0.7 | 0.014912 | 10 | 0.015804 | 100 | 0.057953 | 1000 | 0.227657 | | 0.8 | 0.014920 | | | | | | | | 0.9 | 0.014928 | | | | | | | | 1 | 0.014935 | | | | | | |
|
Residual results of R2 parameters
|

|
Residual curve of R2 parameters
|

| 半径R1=R2 | 标准偏差 | | 6、8、10、11.7、14、16 | 0.014847 |
|
Residual results of search radius in circular neighborhood
|

| 搜索选项 | 对应参数 | | ①搜索扇区个数/个 | 1 | 4 | 8 | | ②从所有扇区使用的最大的数据个数/个 | 64 | 64 | 64 | | ③从每个扇区使用的最大的数据个数/个 | 64 | 16 | 8 | | ④所有扇区的最小数据个数(更少则白化节点)/个 | 8 | 8 | 8 | | ⑤如果空白扇区多于此数则白化节点/个 | 1 | 3 | 7 |
|
Search sectors and search points
|
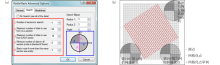
|
Search interface options (a) and search points distribution (b)
|

|
Different search angle icons
|

| 搜索扇区1个 | 搜索扇区4个 | 搜索扇区8个 | | 搜索角度=各向异性角度 | 标准偏差 | 搜索角度=各向异性角度 | 标准偏差 | 搜索角度=各向异性角度 | 标准偏差 | | 0° | 0.014645 | 0° | 0.014847 | 0° | 0.014833 | | 32° | 0.014645 | 32° | 0.014311 | 32° | 0.014827 | | 45° | 0.014645 | 45° | 0.014776 | 45° | 0.014833 | | 90° | 0.014645 | 90° | 0.014847 | 90° | 0.014833 | | 122° | 0.014645 | 122° | 0.014311 | 122° | 0.014827 | | 135° | 0.014645 | 135° | 0.014776 | 135° | 0.014833 |
|
Residual results of different search sectors in circular neighborhood
|

|
Residual curves of different search sectors in circular neighborhood
|

| 参数设置条目 | A组 | B组 | C组 | D组 | E组 | F组 | G组 | | 从所有扇区使用的最大的数据个数 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | | 从每个扇区使用的最大的数据个数 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | | 所有扇区的最小数据个数(更少则白化节点) | 8 | 8 | 8 | 8 | 8 | 8 | 8 | | 如果空白扇区多于此数则白化节点 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
|
Maximum number data of 4 search sectors in circular neighborhood
|

|
Residual results and curve of maximum number data of 4 search sectors in circular neighborhood
|

分
类 | 搜索半径
R1~R2 | 各向异性比
率=R1/R2 | 各向异性角度=搜索角度 | | 0° | 32° | 45° | 90° | 122° | 135° | | A类 | 6~12 | 0.5 | 0.015916 | 0.018210 | 0.016184 | 0.014729 | 0.014776 | 0.014756 | | B类 | 6~9 | 0.667 | 0.014668 | 0.015528 | 0.015483 | 0.014895 | 0.014786 | 0.014899 | | C类 | 9~6 | 1.5 | 0.014873 | 0.014765 | 0.014852 | 0.014689 | 0.015694 | 0.015587 | | D类 | 12~6 | 2 | 0.014672 | 0.014756 | 0.014723 | 0.015882 | 0.019098 | 0.016929 |
|
Residual results of different parameters of 1 search sector in elliptical neighborhood
|

分
类 | 搜索半径
R1~R2 | 各向异性比
率=R1/R2 | 各向异性角度=搜索角度 | | 0° | 32° | 45° | 90° | 122° | 135° | | A类 | 6~12 | 0.5 | 0.015553 | 0.020861 | 0.015845 | 0.014718 | 0.014723 | 0.014730 | | B类 | 6~9 | 0.667 | 0.014799 | 0.014106 | 0.015380 | 0.014883 | 0.014755 | 0.014870 | | C类 | 9~6 | 1.5 | 0.014850 | 0.014735 | 0.014825 | 0.014822 | 0.014330 | 0.015475 | | D类 | 12~6 | 2 | 0.014660 | 0.014698 | 0.014702 | 0.015532 | 0.021106 | 0.016584 |
|
Residual results of different parameters of 4 search sectors in elliptical neighborhood
|

分
类 | 搜索半径
R1~R2 | 各向异性比
率=R1/R2 | 各向异性角度=搜索角度 | | 0° | 32° | 45° | 90° | 122° | 135° | | A类 | 6~12 | 0.5 | 0.015604 | 0.016997 | 0.017085 | 0.014793 | 0.014747 | 0.014735 | | B类 | 6~9 | 0.667 | 0.014908 | 0.014409 | 0.015404 | 0.014794 | 0.014797 | 0.014857 | | C类 | 9~6 | 1.5 | 0.014764 | 0.014758 | 0.014822 | 0.014924 | 0.014575 | 0.015488 | | D类 | 12~6 | 2 | 0.014721 | 0.014718 | 0.014715 | 0.015600 | 0.017782 | 0.017769 |
|
Residual results of different parameters of 8 search sectors in elliptical neighborhood
|

|
Residual curves of different parameters of 1 search sector in elliptical neighborhood
|

|
Residual curves of different parameters of 4 search sectors in elliptical neighborhood
|

|
Residual curves of different parameters of 8 search sectors in elliptical neighborhood
|

|
Residual results and curve of maximum number data of 4 search sectors in elliptical neighborhood
|

|
Residual results and curve of same search radius in circular neighborhood
|

|
Map of the interpolation points distribution with the same search radius
|

|
Residual results and curve of different search radius in elliptical neighborhood
|

|
Map of the interpolation points distribution with the different search radius
|
| [1] |
张伟, 覃庆炎, 简兴祥. 自然邻点插值算法及其在二维不规则数据网格化中的应用[J]. 物探化探计算技术, 2011, 33(3):291-295.
|
| [1] |
Zhang W, Qin Q Y, Jian X X. Natural neighbour interpolation and its application to 2D grid of irregular data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2011, 33(3):291-295.
|
| [2] |
向文. 重力插值方法研究[J]. 地壳形变与地震, 1997, 17(2):59-64.
|
| [2] |
Xiang W. Research on interpolation methods in gravity field[J]. Crustal Deformation and Earthquake, 1997, 17(2):59-64.
|
| [3] |
郭良辉, 孟小红, 郭志宏, 等. 地球物理不规则分布数据的空间网格化法[J]. 物探与化探, 2005, 29(5):438-442.
|
| [3] |
Guo L H, Meng X H, Guo Z H, et al. Gridding methods of geophysical irregular data in space domain[J]. Geophysical and Geochemical Exploration, 2005, 29(5):438-442.
|
| [4] |
王万银, 邱之云. 一种稳定的位场数据最小曲率网格化方法研究[J]. 地球物理学进展, 2011, 26(6):2003-2010.
|
| [4] |
Wang W Y, Qiu Z Y. The research to a stable minimum curvature gridding method in potential data processing[J]. Progress in Geophysics, 2011, 26(6):2003-2010.
|
| [5] |
陈耀坤, 张益民, 曹绪宏, 等. 大面积物探数据的网格化处理方法[J]. 地质与勘探, 1984(3):34-41.
|
| [5] |
Chen Y K, Zhang Y M, Cao X H, et al. Grid processing method of large area geophysical data[J]. Geology and Prospecting, 1984 (3):34-41.
|
| [6] |
郭志宏. 一种实用的等值线型数据网格化方法[J]. 物探与化探, 2001, 25(3):203-208.
|
| [6] |
Guo Z H. A practical contour type data gridding technique[J]. Geophysical and Geochemical Exploration, 2001, 25(3):203-208.
|
| [7] |
李振海, 汪海洪. 重力数据网格化方法比较[J]. 大地测量与地球动力学, 2010, 30(1):140-144.
|
| [7] |
Li Z H, Wang H H. Comparison among methods for gravity data gridding[J]. Journal of Geodesy and Geodynamics, 2010, 30(1):140-144.
|
| [8] |
中华人民共和国国土资源部. DZ/T 0004—2015重力调查技术规范(1∶50000)[S]. 北京: 地质出版社, 2015.
|
| [8] |
Ministry of Land and Resources of the People's Republic of China. DZ/T 0004—2015 The technical specification for gravity survey (1∶50000)[S]. Beijing: Geological Publishing House, 2015.
|
| [9] |
王兆国, 程顺有, 刘财. 地球物理勘探中几种二维插值方法的误差分析[J]. 吉林大学学报:地球科学版, 2013, 43(6):1997-2004.
|
| [9] |
Wang Z G, Cheng S Y, Liu C. Error analysis of several two-dimensional interpolation methods in the geophysical exploration[J]. Journal of Jilin University:Earth Science Edition, 2013, 43(6):1997-2004.
|
| [10] |
许海红, 卢进才, 李玉宏, 等. 基于Surfer的1∶50000规则测网重力数据网格化方法选取——以银额盆地赛汉陶来区块重力资料为例[J]. 地球物理学进展, 2015, 30(6):2566-2573.
|
| [10] |
Xu H H, Lu J C, Li Y H, et al. Selection of gridding methods for 1∶50000 regular-grid gravity data based on surfer—A case from gravity data in Saihantaolai block of Yin’e basin[J]. Progress in Geophysics, 2015, 30(6):2566-2573.
|
| [11] |
王玉敏, 冯宁, 姚敏. 地球物理数据网格化参数的确定及模型的选择[J]. 山东国土资源, 2015, 31(10):86-90.
|
| [11] |
Wang Y M, Feng N, Yao M. The Determination about the grid parameters of geophysical data and the selection about the grid model[J]. Shandong Land and Resources, 2015, 31(10):86-90.
|
| [12] |
王美丁, 马见青, 樊金生. 基于Surfer软件的数据网格化方法探析[J]. 工程地球物理学报, 2017, 14(6):694-700.
|
| [12] |
Wang M D, Ma J Q, Fan J S. The discussion on the geophysical data gridding based on the surfer software[J]. Chinese Journal of Engineering Geophysics, 2017, 14(6):694-700.
|
| [13] |
高艳芳, 陈实, 冯斌. 交叉验证在离散数据网格化时的应用[J]. 物探化探计算技术, 2012, 34(5):619-621.
|
| [13] |
Gao Y F, Chen S, Feng B. Using cross validation in gridding[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2012, 34(5):619-621.
|
| [14] |
杜红悦, 张浚哲, 宫辉力. DEM产品数据质量分析研究与系统实现[J]. 测绘科学, 2009, 34(4):191-194.
|
| [14] |
Du H Y, Zhang J Z, Gong H L. Research of DEM quality-precision analysis and system implementation[J]. Science of Surveying and Mapping, 2009, 34(4):191-194.
|
| [15] |
张锦明, 游雄, 万刚. 径向基函数算法中插值参数对DEM精度的影响[J]. 武汉大学学报·信息科学版, 2013, 38(5):608-612.
|
| [15] |
Zhang J M, You X, Wan G. Effects of interpolation parameters in multi-log radial basis function on DEM accuracy[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5):608-612.
|
| [16] |
张锦明, 游雄, 万刚. DEM插值参数优选的试验研究[J]. 测绘学报, 2014, 43(2):178-185,192.
|
| [16] |
Zhang J M, You X, Wan G. Experimental research on optimization of DEM interpolation parameters[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2):178-185, 192.
|
| [17] |
白世彪, 王建, 常直杨. Surfer10地学计算机制图[M]. 北京: 科学出版社, 2012.
|
| [17] |
Bai S B, Wang J, Chang Z Y. Surfer10 Geoscience Computer Mapping [M]. Beijing: Science Press, 2012.
|
| [18] |
高艳芳. 离散数据网格化参数的确定和数学模型的选择——以Surfer7.0、Mapgis6.0为例[J]. 地质与勘探, 2002, 38(S):139-142.
|
| [18] |
Gao Y F. Specifying the parameters of gridding and choosing gridding algorithm[J]. Geology and Prospecting, 2002, 38(S):139-142.
|
| [19] |
张志厚, 徐世浙, 余海龙, 等. 位场向下延拓的迭代法的扩边方法[J]. 浙江大学学报:工学版, 2013, 47(5):918-924.
|
| [19] |
Zhang Z H, Xu S Z, Yu H L, et al. Study of extending methods of iteration of downward continuation in potential field[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(5):918-924.
|
| [20] |
吴太旗, 黄谟涛, 欧阳永忠, 等. 高精度海洋重力异常格网插值技术研究[J]. 测绘科学, 2008, 33(5):70-72.
|
| [20] |
Wu T Q, Huang M T, Ouyang Y Z, et al. The study of high precision interpolation technology in marine gravity anomaly[J]. Science of Surveying and Mapping, 2008, 33(5):70-72.
|
| [21] |
宁津生, 李金文, 晁定波. 各向异性局部重力场计算的谱方法[J]. 武汉测绘科技大学学报, 1998, 23(3):227-229,278.
|
| [21] |
Ning J S, Li J W, Chao D B. The spectral methods for computation of non-isotropic local gravity field[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(3):227-229, 278.
|
|
|
|

