|
|
|
| Interpolation of potential-field data by Projection Onto Convex Sets algorithm with generalized exponential threshold and based on Discrete Cosine Transform |
AI Han-Bing( ), WANG Yan-Guo( ), WANG Yan-Guo( ) ) |
| School of Geophysical and Measurement-Control Technology, East China University of Technology,Nanchang 330013, China |
|
|
|
|
Abstract Data filling or interpolation is a fundamental and vital problem of potential-field data processing. Some data cannot be measured when some places are unable to reach, such as rivers, or cliffs. If we want to acquire the missing data for better subsequent processing, we need to interpolate or fill in the missing data. Hence, this article introduces the Discrete Cosine Transform (DCT) method into the Projection Onto Convex Sets (POCS) algorithm to tackle this problem, and a generalized exponential threshold attenuation method is also given. Finally, model tests and practical applications show that the POCS algorithm with generalized exponential threshold and based on DCT has the advantages of high accuracy, small filling or interpolating traces and the noise standard of the filled data are closer to real situation.
|
|
Received: 04 January 2021
Published: 21 December 2021
|
|
|
|
Corresponding Authors:
WANG Yan-Guo
E-mail: 1724178612@qq.com;wangyg8503@126.com
|
|
|
|
10]
">
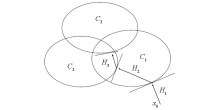
|
The mechanism of POCS method[10]
|
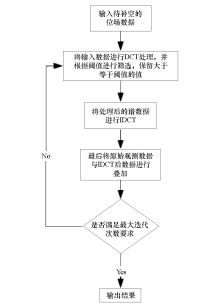
|
The flow-process diagram of POCS method to interpolate based on DCT
|

| 模型编号 | 模型类型 | x方向范围/m | y方向范围/m | z方向范围/m | 密度/(g·cm-3) | | Model 1 | 圆柱体 | -200~200 | -190~-110 | 10~90 | 2 | | Model 2 | 棱柱体 | -50~50 | -50~50 | 20~400 | -2 | | Model 3 | 棱柱体 | -200~0 | 100~200 | 30~1000 | 2 | | Model 4 | 球体 | 100~200 | 100~200 | 10~110 | 2 |
|
Model parameters
|
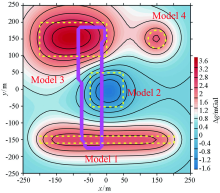
|
Forward gravity anomaly with complete data and the target zone (pink part)
|
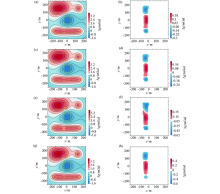
|
Results of interpolation using conventional methods and the differences with the original data
a、b—interpolated result of Kriging and its residuo;c、d—interpolated result of radial basis function and its residuo;e、f—interpolated result of inverse distance to a power and its residuo;g、h—interpolated result of minimum curvature and its residuo
|

| 处理方法 | 均方根误差/mGal | | 克里金法 | 0.123 | | 径向基函数法 | 0.113 | | 反距离加权法 | 0.285 | | 最小曲率法 | 0.217 |
|
RMS errors of interpolating data using different conventional interpolation methods
|

|
The relationship between the errors of interpolating data by using POCS with different threshold models and the total number of iterations
|
|
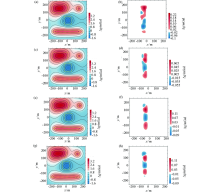
Results of interpolation using POCS method with linear and exponential threshold and the difference with the original data (K=800)
a、b—interpolated result using linear threshold and its residuo;c、d—interpolated result using exponential threshold (Para=0.5) and its residuo;e、f—interpolated result using exponential threshold (Para=1) and its residuo;g、h—interpolated result using exponential threshold (Para=2) and its residuo
|
Fig. 3
">
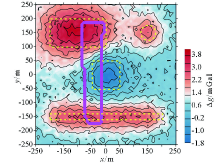
|
Gravity anomaly and missing site after adding 30% random noise of Fig. 3
|
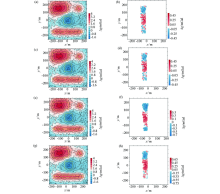
|
Results of interpolating noise-corrupted data using conventional interpolation methods and the difference with the original noise-free data
a、b—interpolated result of Kriging and its residuo;c、d—interpolated result of radial basis function and its residuo;e、f—interpolated result of inverse distance to a power and its residuo;g、h—interpolated result of minimum curvature and its residuo
|

| 插值方法 | 均方根误差/mGal | | 克里金法 | 0.191 | | 径向基函数法 | 0.185 | | 反距离加权法 | 0.315 | | 最小曲率法 | 0.280 |
|
RMS errors of interpolating noise-corrupted data using different conventional interpolation methods
|

|
The relationship between the errors of interpolation data using POCS with different threshold models for the noise-corrupted data and the total number of iterations
|
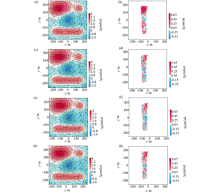
|
Results of interpolation using POCS method with linear and exponential threshold model and the differences with the noise-free data
a、b—interpolated result using linear threshold and its residuo;c、d—interpolated result using exponential threshold (Para=0.5) and its residuo;e、f—interpolated result using exponential threshold (Para=1) and its residuo;g、h—interpolated result using exponential threshold (Para=2) and its residuo
|
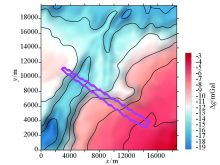
|
Bouguer gravity anomaly of Nenbei Farm in Heilongjiang Province and the target zone (pink part)
|
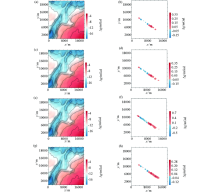
|
Results of interpolation using conventional methods and the differences with the real data
a、b—interpolated result of Kriging and its residuo;c、d—interpolated result of radial basis function and its residuo;e、f—interpolated result of inverse distance to a power and its residuo;g、h—interpolated result of minimum curvature and its residuo
|

| 处理方法名称 | 均方根误差/mGal | | 克里金法 | 0.105 | | 径向基函数法 | 0.091 | | 反距离加权法 | 0.298 | | 最小曲率法 | 0.105 |
|
The errors of interpolation results using conventional methods for the read data
|

|
The relationship between the errors of interpolating data using POCS with different threshold models and the total number of iterations
|

|
Using exponential threshold-based POCS method to interpolate real field data
a—interpolated result (Para=0.5);b—the residuo (K=6500)
|
| [1] |
孙洪泉. 地质统计学及其应用[M]. 北京: 中国矿业大学出版社, 1990.
|
| [1] |
Sun H Q. Geological statistics and its application [M]. Beijing: China University of Mining and Technology Press, 1990.
|
| [2] |
Briggs I C. Machine contouring using minimum curvature[J]. Geophysics, 1974, 39(1):39-48.

|
| [3] |
Cordell L. A scattered equivalent-source method for interpolation and gridding of potential-field data in three dimensions[J]. Geophysics, 1992, 57(4):629-636.

|
| [4] |
郭志宏. 一种使用的等值线型数据网格化方法[J]. 物探与化探, 2001, 25(3):203-208.
|
| [4] |
Guo Z H. A practical contour type data gridding technique[J]. Geophysical and Geochemical Exploration, 2001, 25(3):203-208.
|
| [5] |
闫浩飞, 刘国峰, 薛典军, 等. 基于凸集投影方法的重磁数据规则缺失重建[J]. 地球物理学进展, 2016, 31(5):2192-2197.
|
| [5] |
Yan H F, Liu G F, Xue D J, et al. Reconstruction of gravity/magnetic data with the projection-onto-convex-sets methods[J]. Progress in Geophysics, 2016, 31(5):2192-2197.
|
| [6] |
王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4):1327-1338.
|
| [6] |
Wang W Y, Qiu Z Y, Liu J L, et al. The research to the extending edge and interpolation based on the minimum curvature method in potential field data processing[J]. Progress in Geophysics, 2009, 24(4):1327-1338.
|
| [7] |
王明, 刘前坤, 李芳, 等. 基于热传导模型位场网格数据补空方法研究[J]. 物探与化探, 2015, 39(S1):144-151.
|
| [7] |
Wang M, Liu Q K, Li F, et al. Filling grid dummy values by heat conduction model[J]. Geophysical and Geochemical Exploration, 2015, 39(S1):144-151.
|
| [8] |
曾小牛, 李夕海, 刘继昊, 等. 基于凸集投影的重力数据扩充下延一体化方法[J]. 石油地球物理勘探, 2019, 54(5):1166-1173.
|
| [8] |
Zeng X N, Li X H, Liu J H, et al. An integration of interpolation, edge padding, and downward continuation for gravity data based on the projection onto convex sets[J]. Oil Geophysical Prospecting, 2019, 54(4):1166-1173.
|
| [9] |
曾小牛, 李夕海, 侯维君, 等. 基于凸集投影的重力同时填充扩边和去噪方法[J]. 石油地球物理勘探, 2020, 55(1):197-205.
|
| [9] |
Zeng X N, Li X H, Hou W J, et al. Simultaneous interpolation, edge padding and denoising method for gravity data based on the projection onto convex sets[J]. Oil Geophysical Prospecting, 2020, 55(1):197-205.
|
| [10] |
Gao J J, Chen X H, Li J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3):229-238.

|
| [11] |
张华, 陈小宏. 基于jitter 采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 2013, 56(5):1637-1649.
|
| [11] |
Zhang H, Chen X H. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese J. Geophys., 2013, 56(5):1637-1649.
|
|
|
|

