|
|
|
| Discussion about the theoretical basis of the down-hole method for shear wave velocity test under surface forward and reverse horizontal hammer strikes |
XIAO Yan-Shan1( ), ZHOU Zheng-Hua1( ), ZHOU Zheng-Hua1( ), SU Jie1, WEI Xin2 ), SU Jie1, WEI Xin2 |
1. Collage of Transportation Engineering,Nanjing Tech University,Nanjing 210009,China
2. First Affiliated Hospital,Heilongjiang University of Chinese Medicine,Harbin 150040,China |
|
|
|
|
Abstract The down-hole method under surface horizontal forward and reverse hammer excitation is frequently used for on-site tests of shear wave velocity.Based on the dynamic finite element method,this paper establishes a three-dimensional analysis model of the down-hole method used for shear wave velocity tests under the surface horizontal forward and reverse hammer excitation.Meanwhile,it determines the solutions of the wave response of linear elastic half space under the surface horizontal hammer excitation through explicit stepwise integration of time-domain lumped mass dynamic finite element.Furthermore,it analyzes the waveform characteristics of points at different depths and the rationality of the theoretical basis of shear wave (S-wave) velocity tests under the surface horizontal forward and reverse hammer excitation.As indicated by the results,the theoretical basis of S-wave velocity tests (i.e.,the non-inversion of P-wave onset but inversion of S-wave onset) using the down-hole method under surface horizontal forward and reverse hammer excitation is not tenable.In addition,the numerical simulation results have been further verified reasonable by the analytical solution of the wave motion in the linear elastic half space under the surface horizontal forward and reverse excitation.
|
|
Received: 13 January 2021
Published: 15 December 2021
|
|
|
|
Corresponding Authors:
ZHOU Zheng-Hua
E-mail: 954231383@qq.com;bjsmoc@163.com
|
|
|
|
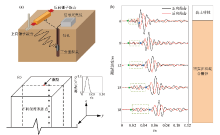
|
Surface level positive and negative percussion hole method S-wave velocity test
a—schematic of downhole seismic method with surface plank source;b—signal traces recorded at different testing depth by downhole seismic method at a site in Beijing;c—3D numerical analysis model of downhole seismic method
|

| vs/(m·s-1) | vp/(m·s-1) | 弹性模量E/Pa | 泊松比μ | ρ/(kg·m-3) | | 200 | 663.3 | 2.204×108 | 0.45 | 1900 |
|
Mechanical parameters of the model
|
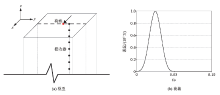
|
3D analysis model(a) and load(b) of S-wave velocity test by hole method under surface horizontal excitation
|
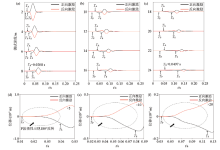
|
Signal traces at different depth observation points in x-direction under the horizontal forward and backward excitation
a、b、c—the original signal traces at different selected depth;d、e、f—amplified waveform of partially signals at observation points with depth of 8 m,16 m,24 m
|

|
Displacements of directly below surface tangential point source with approximate Heaviside unit function
a—approximate Heaviside unit function;b—displacements at depth of 2 m and 8 m in an elastic half-space directly below surface tangential point source with the poisson's ratio of 0.25
|
| [1] |
汪闻韶. 土工地震减灾工程中的一个重要参量——剪切波速[J]. 水利学报, 1994, 15(3):80-83.
|
| [1] |
Wang W S. An important parameter in geotechnical engineering for earthquake disaster mitigation—shear wave velocity[J]. Journal of Hydraulic Engineering, 1994, 15(3):80-83.
|
| [2] |
毕兴锁. 场地剪切波速在岩土工程中的应用[J]. 山西建筑, 1992(1):23-29.
|
| [2] |
Bi X S. Application of site shear wave velocity in geotechnical engineering[J]. Shanxi Architecture, 1992(1):23-29.
|
| [3] |
陈昌军. 场地剪切波波速测试及其应用[J]. 华南地震, 2003, 23(4):81-86.
|
| [3] |
Chen C J. Shear wave velocity testing of building site and its application[J]. South China Journal of Seismology, 2003, 23(4):81-86.
|
| [4] |
Hunter J A, Pullan S E, Burns R A, et al. Downhole seismic logging for high-resolution reflection surveying in unconsolidated overburden[J]. Geophysics, 1998, 63(4):1371-1384.

|
| [5] |
Hunter J A, Benjumea B, Harris J B, et al. Surface and downhole shear wave seismic methods for thick soil site investigations[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(9-12):931-941.

|
| [6] |
Schneider J A, Mayne P W, Rix G J. Geotechnical site characterization in the greater Memphis area using cone penetration tests[J]. Engineering Geology, 2001, 62(1-3):169-184.

|
| [7] |
Kayabasi A, Gokceoglu C. Liquefaction potential assessment of a region using different techniques (Tepebasi,Eskiᶊehir,Turkey)[J]. Engineering Geology, 2018, 246:139-161.

|
| [8] |
Stokoe K H, Joh S H, Woods R D. Some contributions of in situ geophysical measurements to solving geotechnical engineering problems[C]// International site characterization ISC'2 Porto,Portugal, 2004:19-42.
|
| [9] |
Garofalo F, Foti S, Hollender F, et al. InterPACIFIC project:Comparison of invasive and non-invasive methods for seismic site characterization.Part II:Inter-comparison between surface-wave and borehole methods[J]. Soil Dynamics & Earthquake Engineering, 2016, 82:241-254.
|
| [10] |
陈云敏, 吴世明, 曾国熙. 表面波谱分析法及其应用[J]. 岩土工程学报, 1992, 14(3):61-65.
|
| [10] |
Chen Y M, Wu S M, Zeng G X. The spectral analysis of surface waves and its application[J]. Chinese Journal of Geotechnical Engineering, 1992, 14(3):61-65.
|
| [11] |
ASTM. Standard test methods for downhole seismic testing[M]// Pennsylvania:Annual book of ASTM standard, 2007.
|
| [12] |
侯兴民, 杨学山, 廖振鹏, 等. 基于互相关函数的单孔法波速测试优化算法[J]. 岩土力学, 2006, 27(7):1161-1165.
|
| [12] |
Hou X M, Yang X S, Liao Z P, et al. An optimized approach for single-hole method of shear wave velocity measurement based on correlation functions[J]. Rock and Soil Mechanics, 2006, 27(7):1161-1165.
|
| [13] |
Baziw E J. Digital filtering techniques for interpreting seismic cone data[J]. Journal of Geotechnical Engineering, 1993, 119(6):998-1018.

|
| [14] |
Crice D. Borehole shear-wave surveys for engineering site investigations[M]. Saratoga:Geostuff, 2002:1-14.
|
| [15] |
Campanella R G, Stewart W P. Seismic cone analysis using digital signal processing for dynamic site characterization[J]. Canadian Geotechnical Journal, 1992, 29(3):477-486.

|
| [16] |
Ishihara K. Soil behaviour in earthquake geotechnics [M]. Oxford: Clarendon Press, 1996.
|
| [17] |
廖振鹏. 工程波动理论导论(第二版)[M]. 北京: 科学出版社, 2002.
|
| [17] |
Liao Z P. Introduction to wave motion theories in engineering (Second Edition) [M]. Beijing: Science Press, 2002.
|
| [18] |
廖振鹏, 周正华, 张艳红. 波动数值模拟中透射边界的稳定实现[J]. 地球物理学报, 2002, 45(4):533-545.
|
| [18] |
Liao Z P, Zhou Z H, Zhang Y H. Stable implementation of transmitting boundary in numerical simulation of wave motion[J]. Chinese Journal of Geophysics, 2002, 45(4):533-545.
|
| [19] |
周正华, 廖振鹏. 消除多次透射公式飘移失稳的措施[J]. 力学学报, 2001, 33(4):550-554.
|
| [19] |
Zhou Z H, Liao Z P. A mersure for eliminating drift instability of the multi-transmitting formula[J]. Acta Mechanica Sinica, 2001, 33(4):550-554.
|
| [20] |
董青, 周正华, 苏杰, 等. 消除多次透射公式高频振荡失稳的一种措施[J]. 震灾防御技术, 2018, 13(3):571-577.
|
| [20] |
Dong Q, Zhou Z H, Su J, et al. The measure against high frequency oscillating instability of multi-transmitting formula[J]. Technology for Earthquake Disaster Prevention, 2018, 13(3):571-577.
|
| [21] |
Sanchez-Salinero I, Roesset J M, Stokoe K H Ⅱ. Analytical studies of body wave propagation and attenuation [R]. Austin:Geotechnical Engineering Center the University of Texas at Austin, 1986.
|
| [22] |
Aki K, Richards P G. Quantitative seismology theory[M]. Mill Valley:University Science Books, 2002.
|
| [23] |
Chao C C. Dynamical response of an elastic half-space to tangential surface loadings[J]. Journal of Applied Mechanics, 1960, 27(3):559-567.

|
| [1] |
WANG Yu-Cheng, WANG Hong-Hua, SU Peng-Jin, GONG Jun-Bo, XI Yu-He. Simulated detection experiments of underground water supply pipeline leakage based on ground penetrating radar[J]. Geophysical and Geochemical Exploration, 2023, 47(3): 794-803. |
| [2] |
XIAO Shi-Peng, XIONG Gao-Jun, YUAN Meng-Yu, MAO Ming-Qiu, WANG Sheng-Yi, WEI Zeng-Tao. Parameter optimization and imaging of visco-acoustic media using high-order Fourier finite-difference method[J]. Geophysical and Geochemical Exploration, 2022, 46(5): 1207-1213. |
|
|
|
|

