|
|
|
| Agglomerative hierarchical clustering seismic facies analysis based on waveform eigenvector |
Shi-You LIU1, Wei SONG2( ), Ming-Xiong YING1, Wan-Yuan SUN1, Rui WANG1 ), Ming-Xiong YING1, Wan-Yuan SUN1, Rui WANG1 |
1. Zhanjiang Branch,CNOOC Ltd.,Zhanjiang 524057,China
2. College of Geophysics,University of Petroleum of China,Beijing 102249,China |
|
|
|
|
Abstract Conventional seismic facies analysis based on seismic sedimentology principle mainly uses seismic slicing technology to extract RMS amplitude attributes along the target layer.When the signal-to-noise ratio of seismic signals is low and the target layer is thin,the accuracy and reliability of seismic facies analysis will be easily affected.In this study,on the basis of the principle of seismic sedimentology,the feature vectors of seismic waveforms were extracted along stratigraphic slices,and then the Agglomerative Hierarchical Clustering (AHC) method was introduced to classify seismic facies.Waveform AHC is an unsupervised machine learning algorithm.Compared with the traditional method of seismic facies analysis for stratum slices,the method based on waveform clustering considers the amplitude, phase and frequency attributes of seismic signals synthetically through the change of waveform characteristics.It has better anti-noise capability and higher horizontal resolution.The stability and applicability of this method have been proved by physical model data testing and practical data application.It has been proved that this method has a good capability of distinguishing sedimentary facies characteristics,and hence it is a new kind of reservoir facies analysis tool and has a good application prospect.
|
|
Received: 20 March 2019
Published: 22 April 2020
|
|
|
|
Corresponding Authors:
Wei SONG
E-mail: songwei@cup.edu.cn
|
|
|
|

|
Classification results of different connection types in the same data set
a—single connection;b—average connection;c—full connection
|

|
Different connection constraints for the same data set
a—connectionless constraint;b—connectivity constraints
|

|
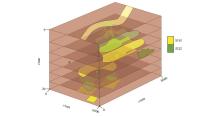
Acquisition size and parameter sketch of physical model
|
|
Spatial distribution diagram of six Layers of sand body in physical model
|

|
Diagram of vertical section of sand overlay model
|

|
Physical model migration profile and horizon interpretation based on seismic sedimentology principle
|

|
200 waveform curves inputted by AHC
|
K=7,waveform vector 31 dimensions);d-waveform AHC(K=7,waveform vector 37 dimensions)
">

|
Sand body planar morphology,RMS amplitude attributes and waveform AHC in the first layer of physical model
a—the plane shape of the first layer of "serpentine" sand body;b—RMS amplitude attributes extracted along stratum slices;c—waveform AHC(K=7,waveform vector 31 dimensions);d-waveform AHC(K=7,waveform vector 37 dimensions)
|
">

|
Spatial distribution and shape of sand and mudstone in the second to fifth layers of physical model
a—planar morphology of "intestinal and finger" sand bodies;b—planar distribution of "intestinal" sand body and "elliptical" mudstone;c—horizontal morphological distribution of dumbbell sand body and finger mudstone;d—plane morphological distribution of "rhombic" sand body and "point" mudstone
|
">

|
Seismic facies division of RMS amplitude attribute of stratum slices
=a—RMS amplitude attribute plane distribution of "intestinal" sand body and "finger" sand body;b—RMS amplitude attribute plane distribution of "intestinal" sand body and "elliptical" mudstone;c—RMS amplitude attribute "dumbbell" sandbody and "finger" mudstone plane distribution;d—RMS amplitude attribute "rhombic" sand body and "point" mudstone plane distribution
|
">

|
Seismic facies division of AHC attribute of stratum slices
a—AHC attribute plane distribution of "intestinal" sand body and "finger" sand body;b—AHC attribute plane distribution of "intestinal" sand body and "elliptical" mudstone;c—AHC attribute "dumbbell" sandbody and "finger" mudstone plane distribution;d—AHC attribute "rhombic" sand body and "point" mudstone plane distribution
|

|
Horizon interpretation based on seismic sedimentology principle in target area
|

|
T70 layer isotropic T0 graph
|

|
RMS amplitude attribute of stratigraphic slices extracted along T70 from prestack time migration data
|

|
AHC attributes obtained by extracting seismic waveforms from prestack time migration data along T70 stratigraphic slices
|
| [1] |
Sloss L L . Stratigraphic models in exploration[J]. AAPG Bulletin, 1962,46(7):1040-1047.
|
| [2] |
Vail P R, Mitchum M, Thompson S , et al. Seismic stratigraphy and global changes of sea level,Part4:Global cycles of relative changes of sea level[G]//C.E.Payton,ed.Seismic stratigraphy applications to hydrocarbon exploration[J]. AAPG Memoir, 1977,26:83-97.
|
| [3] |
Zeng H L, Backus M M, Barrow K T , et al. Stratal slicing,Part I:Realistic 3-D seismic model[J]. Geophysics, 1998,63(2):502-513.
|
| [4] |
Zeng H L, Henry S C, Riola J P . Stratal slicing,Part II:Real 3-D seismic data[J]. Geophysics, 1998,63(2):514-521.
|
| [5] |
Zeng H L, Hentz T F, Wood L J . Stratal slicing of Miocene-Pliocene sediments in Vermilion Block 50-Tiger Shoal area,offshore Louisiana[J]. The Leading Edge, 2001,20(4):408-418.
|
| [6] |
Zeng H L, Ambrose W A . Seismic sedimentology and regional depositional systems in Mioceno Norte,Lake Maracaibo,Venezuela[J]. The Leading Edge, 2001,20(11):1260-269.
|
| [7] |
Zeng H L, Backus M M, Barrow K T , et al. Stratal slicing,Part I:Realistic 3-D seismic model[J]. Geophysics, 1998,63(2):502-513.
|
| [8] |
Zeng H L, Henry S C, Riola J P . Stratal slicing,PartⅡ:Realistic 3-D seismic model[J]. Geophysics, 1998,63(2):514-522.
|
| [9] |
Zeng H L, Hentz T F, Wood L J . Stratal slicing of Miocene-Plioeene sediments in Vermilion Block 50,Tiger Shoal area,offshore Louisiana[J]. The Leading Edge, 2001,20(4):408-418.
|
| [10] |
Hall B . Facies classification using machine learning[J]. The Leading Edge, 2016,36(10):906-909.
|
| [11] |
Bhattacharya S, Carr T R, Pal M . Comparison of supervised and unsupervised approaches for mudstone lithofacies classification:Case studies from the Bakken and Mahantango-Marcellus Shale,USA[J]. Journal of Natural Gas Science & Engineering, 2016,33:1119-1133
|
| [12] |
刘爱群, 陈殿远, 任科英 . 分频与波形聚类分析技术在莺歌海盆地中深层气田区的应用[J]. 地球物理学进展, 2013,28(1):338-344.
|
| [12] |
Liu A Q, Chen D Y, Ren K Y . Frequency decomposition and waveform cluster analysis techniques Yinggehai Basin gas field in the deep area of application[J]. Progress in Geophysics, 2013,28(1):338-344.
|
| [13] |
白博, 舒梦珵, 康洪全 , 等. 基于伪阻抗体波形聚类的贝克灰岩储层预测方法[J]. 物探化探计算技术, 2015,37(6):724-727.
|
| [13] |
Bai B, Shu M C, Kang H Q , et al. Coquina reservoir prediction method of seismic pseudo-impedance waveform clustering[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2015,37(6):724-727.
|
| [14] |
李辉, 罗波, 何雄涛 , 等. 基于地震波形聚类储集砂体边界识别与预测[J]. 工程地球物理学报, 2017,14(5):573-577.
|
| [14] |
Li H, Luo B, He X T , et al. Boundary identification and prediction of sand body based on seismic waveform[J]. Chinese Journal of Engineering Geophysics, 2017,14(5):573-577.
|
| [15] |
徐海, 都小芳, 高君 , 等. 基于波形聚类的沉积微相定量解释技术研究[J]. 石油物探, 2018,57(5):744-755.
|
| [15] |
Xu H, Du X F, Gao J , et al. Quantitative interpretation of sedimentary microfaacies based on waveform clustering:a case study of X oilfield,Middle East[J]. Geophysical Prospecting for Petroleum, 2018,57(5):744-755.
|
| [16] |
张艳, 张春雷, 高世臣 . 基于SOM和HSV染色技术的致密砂岩储层地震相分析[J]. 天然气地球科学, 2018,29(2):259-267.
|
| [16] |
Zhang Y, Zhang C L, Gao S C . Seismic facies analysis of tight sandstone reservoir based on SOM and HSV color techniqu[J]. Natural Gas Geoscience, 2018,29(2):259-267.
|
| [17] |
罗浩然, 尹成, 丁峰 , 等. 概率神经网络的平滑参数分析及在地震属性分析中的应用[J]. 石油物探, 2017,56(4):551-558.
|
| [17] |
Luo H R, Yin C, Ding F , et al. The smoothing parameter analysis of probabilistic neural network and its application[J]. Geophysical Prospecting for Petroleum, 2017,56(4):551-558.
|
| [18] |
魏艳, 尹成, 丁峰 , 等. 地震多属性综合分析的应用研究[J]. 石油物探, 2007,46(1):42-47.
|
| [18] |
Wei Y, Yin C, Ding F , et al. Synthetic analysis of seismic multi-attribute and its application[J]. Geophysical Prospecting for Petroleum, 2007,46(1):42-47.
|
|
|
|

