|
|
|
| A reliable first arrival picking method for high-noise three component microseismic data |
| Yi-Ming CHENG1,4, Huai-Liang LI1,3, Xian-Guo TUO1,2,3, Yao-Bin WANG4, Ya-Juan WANG1, Tong SHEN1,2,3 |
1. Fundamental Science on Nuclear Wastes and Environmental Safety Laboratory,Southwest University of Science and Technology,Mianyang 621010,China
2. Sichuan University of Science & Engineering,Zigong 643002,China;
3. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology,Chengdu 610059,China
4. College of Computer Science and Technology,Southwest University of Science and Technology,Mianyang 621010,China |
|
|
|
|
Abstract Accurate first-arrival picking plays a significant role in microseismic data processing.The dominate methods,i.e.,short-term average to long-term average ratio (STA/LTA) and the autoregressive (AR) model using Akaike Information Criterion (AIC) algorithm,are not optimal for picking up high-noise data.In order to optimize the first-arrival point estimation of high-noise data,the authors propose an improved picking method based on wavelet multi-scale analysis (WMA) and AIC algorithm.In this algorithm,WMA is used to decompose the high-noise three-component (3C) microseismic data,and the actual calculation data are reconstructed based on the approximation data.Then the maximum value of the absolute value is calculated to constrain the AIC calculation data segment;on such a basis,the global minimum value of the AIC sequence is selected as its first arrival point.The improved algorithm is verified by both synthetic data and field data in this paper.The results show that the improved first-arrival picking algorithm can be effectively applied to high-noise three component microseismic data processing and greatly enhance its accuracy(the error range is 0.25~0.5 ms).
|
|
Received: 11 October 2018
Published: 10 April 2019
|
|
|
|
|
|

|
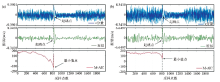
Different AIC values for synthetic microseismic data
a—random noise account for 5%;b—random noise account for 60%;principal frequency of P-wave is 100 Hz,sample interval is 0.25 ms
|
|
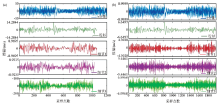
Wavelat multilevel decomposition and reconstruction waveforms using synthetic microseismic data
a—original data and decomposition datasets;b—original data and reconsruction datasets;random noise account for 80%,principal frequency of P-wave is 100 Hz,sample interval is 0.25 ms,decomposition level is 3,mother wavelet is the db10
|
|
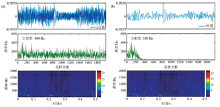
Time-frequency analysis comparison of original data and reconstructed approximation data using the above synthetic microseismic data
a—time-frequency analysis of the original data;b—time-frequency of the reconstructed approximation data
|
|
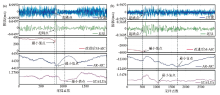
Picking example of improved algorithm using synthetic 3C microseismic data
a—random noise account for 60%;b—random noise account for 80%;principal frequency of P-wave is 100 Hz,sample interval is 0.25 ms,mother wavelet is the db10,decomposition level is 3
|

| 随机噪声 | 最大误差/ms | 拾取数据误差占比/% | | 误差小于等于0.25 ms | 误差小于等于0.5 ms | | 60% | 0.25 | 97 | 100 | | 80% | 0.25 | 95 | 100 | | 90% | 0.50 | 92 | 97 | | 100% | 0.75 | 90 | 95 |
|
First arrival picking error statistics of 100 synthetic 3C microseismic data under different random noise
|
|
Pickup result and comparison among improved M-AIC、STA/LTA and AR-AIC algorithms
a—synthetic 3C microseismic data with 80% random noise;b—field microseismic data
|
| [1] |
刘劲松, 王赟, 姚振兴 . 微地震信号到时自动拾取方法[J]. 地球物理学报, 2013,56(5):1660-1666.

|
| [1] |
Liu J S, Wang Y, Yao Z X . On micro-seismic first arrival identification:A case study[J]. Chinese J. Geophys. (in Chinese), 2013,56(5):1660-1666.
|
| [2] |
Pugh D J, White R S, Christie P A F . Automatic Bayesian polarity determination[J].Geophysical Journal International, 2016(1):146.
|
| [3] |
张唤兰, 朱光明, 王云宏 . 基于时窗能量比和AIC的两步法微震初至自动拾取[J]. 物探与化探, 2013,37(2):269-273.

|
| [3] |
Zhang H L, Zhu G M, Wang Y H . Automatic microseismic event detection and picking method[J]. Geophysical and Geochemical Exploration, 2013,37(2):269-273.
|
| [4] |
Zhu M, Wang L, Liu X , et al. Accurate identification of P- and S-phase arrivals using the multi-step AIC algorithm[J]. Journal of Applied Geophysics, 2018: 150.

|
| [5] |
杨晶惠, 庹先国, 蒋鑫 , 等. 一种具有抗噪性的P波初至自动拾取方法[J].金属矿山, 2015(2):113-116.

|
| [5] |
Yang J H, Tuo X G, Jiang X , et al. A first arrival automatic picking method of P-wave with noise resistence performance[J].Metal mine, 2015(2):113-116.
|
| [6] |
谭玉阳, 于静, 冯刚 , 等. 微地震事件初至拾取SLPEA算法[J]. 地球物理学报, 2016,59(1):185-196.

|
| [6] |
Tan Y Y, Yu J, Feng G , et al. Arrival picking of microseismic events using the SLPEA algorithm[J]. Chinese J. Geophys. (in Chinese), 2016,59(1):185-196.
|
| [7] |
秦晅, 宋维琪 . 基于时窗能量比与互信息量的微地震初至拾取方法[J]. 物探与化探, 2016,40(2):374-379.

|
| [7] |
Qin X, Song W Q . Automatic first arrival pickup method of microseismic event based on energy ratio and mutual information[J]. Geophysical and Geochemical Exploration, 2016,40(2):374-379.
|
| [8] |
贾瑞生, 谭云亮, 孙红梅 , 等. 低信噪比微地震P波震相初至自动拾取方法[J]. 煤炭学报, 2015,40(8):1845-1852.
|
| [8] |
Jia R S, Tan Y L, Sun H M , et al. Method of automatic detection on micro-seismic P-arrival time under low signal to noise ratio[J]. Journal of China Coal Society, 2015,40(8):1845-1852.
|
| [9] |
Li H, Tuo X, Shen T , et al. A new first break picking for three-component VSP data using gesture sensor and polarization analysis[J]. Sensors, 2017,17(9):2150.

|
| [10] |
Maeda N . A method for reading and checking phase times in autoprocessing system of seismic data[J]. Zisin, 1985,38:365-380.

|
| [11] |
沈统, 庹先国, 李怀良 , 等. 利用偏振约束对最小信息准则方法自动拾取微地震初至的改进[J]. 科学技术与工程, 2017,17(23):26-30.

|
| [11] |
Shen T, Tuo X G, Li H L , et al. An improved AIC method for automatic micro-seismic data arrival picking with the constraint by polarization[J]. Science Technology and Engineering, 2017,17(23):26-30.
|
| [12] |
宋维琪, 吕世超 . 基于小波分解与Akaike信息准则的微地震初至拾取方法[J]. 石油物探, 2011,50(1):14-21.

|
| [12] |
Song W Q, Lv S C . Automatic detection method of microseismic event based on wavelet decomposition and Akaike information criteria[J]. Geophysical Prospecting for Petroleum, 2011,50(1):14-21.
|
| [13] |
Mousavi S M, Langston C A . Hybrid seismic denoising using higher-order statistics and improved wavelet block thresholding, Bulletin of the Seismological Society of America 106, 2016: 1380-1393.
|
| [14] |
牟力, 陈召曦 . 重力资料多尺度分析最优小波基的选择[J]. 物探与化探, 2015,39(5):1013-1019.

|
| [14] |
Mou L, Chen Z X . The optimal choice of wavelet bases in gravity data multi-scale analysis[J]. Geophysical and Geochemical Exploration, 2015,39(5):1013-1019.
|
| [15] |
Führ H, Tousi R R . Simplified vanishing moment criteria for wavelets over general dilation groups, with applications to abelian and shearlet dilation groups[J]. Applied and Computational Harmonic Analysis 43, 2017: 449-481.

|
| [16] |
Aguilera E, Nannini M, Reigber A . Wavelet-based compressed sensing for SAR tomography of forested areas[J]. IEEE Transactions on Geoscience and Remote Sensing 51, 2013: 5283-5295.

|
|
|
|
